앞의 글 “시간 단위 측정 [1]“에서 설명한 바대로, 측정하기 위해서는 “눈금”이 있어야 하며, 시간의 경우 그 눈금은 “초second”(단위로는 “s”라고 쓴다)이다. 특히 일정한 시간이 지난 후 원래 상태로 돌아오는 주기 운동의 경우, 원래의 상태로 돌아오는 데 걸리는 시간을 “주기”라고 하고, 그 단위는 “초”이다. 그리고 1초 동안의 주기 운동의 개수를 “진동수” 혹은 “주파수”라고 하며, 그 단위는 “Hz”이다. 처음으로 전자기파의 존재를 증명한 독일의 과학자 하인리히 헤르츠Heinrich Hertz의 이름을 붙여 지은 이름이다. 원래는 초당 주기 운동의 개수를 직접적으로 표현하여 cpscycles per second라는 단위를 사용하였으나, 1960년 Hz로 바뀌게 되었다. 가끔 과거의 문헌을 보면 cps라는 단위를 사용하는데 이는 지금의 Hz와 동일하다.
현재 모든 SI 단위의 정의는 국제도량형사무국BIPM(Bureau International des Poids et Measures(불어), International Bureau of Weights and Measures(영어))의 SI 브로셔SI Brochure에 정의되어 있다. 이에 따르면 “초”는 세슘주파수 ΔνCs의 값을 Hz 단위로 나타내었을 때 9,192,631,770으로 고정함으로써 정의한다. 여기서 세슘주파수 ΔνCs는 세슘 133 원자의 섭동perturbation이 없는 바닥 상태ground-state의 초미세 구조hyperfine structure 사이의 전이주파수이다. 정의를 읽어도 무슨 말인지 알기 쉽지 않다. 일단 다음 단락에서 이 정의가 뜻하는 바를 먼저 설명하고자 한다. 그리고 이후에 실제로 이를 어떻게 구현하는지 원리적으로 살펴보고, 피할 수 없는 주변 환경의 영향으로 인해 생기는 불확도에 대해 알아보고자 한다.
1초의 정의: 세슘원자의 주파수
먼저 위의 정의를 풀어서 설명해 보자. 일단 세슘부터. 세슘이라는 원자는 주기율표상의 1족에 해당하는 원소이다. 여러 동위원소가 존재하며, 그중 가장 안정적인 원자량 133의 세슘원자를 초의 정의에 사용한다. 세슘 133원자의 핵은 양성자 55개, 중성자 78개로 이루어져 있다. 그리고 전자는 총 55개가 있는데, 그중 54개는 매우 안정적인 위치에 있고, 가장 바깥의 1개 전자(“최외곽 전자”라 불리지만, 이후에는 혼동의 여지가 없으면, 그냥 “전자”로 부르기로 한다)가 전자기파를 흡수하여 여러 높은 에너지 층level을 오갈 수 있다.
에너지 층은 마치 계단처럼 구별된, 전자가 머물 수 있는 에너지 상태로서, [그림1]과 같이 한 원자 내에 여러 개가 존재하며, 위로 갈수록 에너지가 높은 상태에 해당한다.보통 전자는 가장 낮은 에너지 상태에 있게 되며 이를 “바닥 상태ground-state“라고 한다. [그림1]의 왼쪽의 맨 아래층에 해당한다. 전자는 한 층에서 다른 층으로만 이동할 수 있으며, 중간 상태는 존재하지 않는다. 그리고 원하는 층으로 이동하기 위해서는 정확하게 두 층 사이의 에너지 차이에 해당하는 에너지를 가진 전자기파를 흡수해야만 이동하게 된다(양자역학에 따라 움직이는 전자의 성질이다). 이렇게 높은 에너지 준위로 전자가 이동한 상태를 “들뜬 상태excited state“라 표현한다. 그리고 바닥 상태도 원자핵의 영향으로 더 세밀하게 나뉘게 되는데 이를 “초미세구조hyperfine structure”라고 부른다([그림1]의 오른 쪽 맨 아래 두 개의 층 1과 2). 비록 둘 중 하나가 에너지가 높지만 둘 다 “바닥 상태”에 있기 때문에, 어느 한 에너지 층에 머물게 되면 거의 영원히 거기 머물 수 있는 안정한 에너지 층이다. 그렇기 때문에 이 둘 사이의 에너지 차이는 매우 정밀하게 측정할 수 있으며, 위의 정의에 따라 정확하게 9,192,631,770 Hz이다. 그리고 “섭동이 없는” 바닥 상태란, 주위에 어떤 영향도 없는 상황에서의 에너지 차이 값이라는 뜻이다. 하지만 실제로 구현할 때는, 온도, 자기장 등 주변의 영향이 항상 존재하기 때문에, 이를 적절히 평가하는 과정이 필요하며, 모든 환경을 완벽하게 통제하거나 알 수 없기 때문에, 주파수를 정확하게 모르는 정도에 해당하는 “불확도” 개념이 원자시계에 등장하게 된다.
1초의 구현: 원자시계
그렇다면 이제 위의 정의로부터 어떻게 1초를 구현할 수 있을까? 가장 간단한 방법은 9,192,631,770 Hz 신호를 만든 다음 이를 원자에 조사하여, 전자가 들뜬 상태로 가는지 살펴 보면서 그 주파수를 조정하면 되고, 1초는 이 주파수를 9,192,631,770으로 나누면 얻을 수 있다. 이것이 앞의 글에서 설명한 원자시계의 기본 원리이다. [그림2]에서 보듯 원자시계는 크게 국부발진기local oscillator와 물리부 그리고 1초를 만들어내는 부분으로 이루어져 있다.
먼저 국부발진기는 원자시계 동작에 필요한 주파수를 만들어 내는 부분이다. 보통은 약 9.2 GHz (1 GHz=109 Hz)의 마이크로파Microwave, MW 대역의 신호를 직접 만들지 않고, [그림2]와 같이 만들기 쉬운 라디오 주파수Radio frequency, RF 대역인 10 MHz(1 MHz = 106 Hz) 신호로부터 주파수 합성기를 통해 9,192,631,770 Hz를 만들어 사용한다. 그리고 10 MHz 신호를 107로 나누게 되면 1초가 만들어 지게 된다. 이후에 설명하겠지만, 보통 세슘원자의 주파수를 확인하기 위해서는 복잡한 과정을 거쳐야 하므로 연속적으로 측정을 하기 어렵다. 따라서 측정과 측정 사이에 10 MHz 신호의 주파수가 많이 벗어나서는 안 된다. 그래서 보통 원자시계 동작에 사용하는 10 MHz를 생성하는 진동자는 일반적인 시계에 사용하는 진동자보다 훨씬 안정도가 높은 진동자를 사용한다. 다만 정확도는 중요하지 않다. 왜냐하면 세슘원자를 통해 정확한 주파수를 알 수 있기 때문이다. 보통은 수소메이저Hydrogen maser와 같은 상용으로 판매되는 원자시계들을 사용한다. 이러한 시계의 경우 1초에 보통 10-13의 상대적인 주파수 안정도를 가지고 있다. 10 MHz 의 출력을 낸다고 가정하면 1초에 10 MHz x 10-13 = 10-6 Hz = 1 \(\mu\)Hz 정도가 흔들린다.
그리고 물리부는 실제로 세슘원자가 자리하여, 국부발진기에서 만들어진 주파수를 측정하는 부분이다. 먼저 원하는 세슘원자만을 어떻게 잘 모아서 준비하는지 설명하고, 준비된 세슘원자로부터 어떻게 정확한 공진주파수 정보를 얻어내는지 알아본다.
먼저 상온에서 고체상태인 세슘만을 모으기 위해서는 깨끗한 환경이 필요하며, 이를 위해 진공챔버를 제작하여, 여기에 세슘을 넣은 다음, 다른 기체 성분을 진공펌프를 이용하여 다 제거한다. 남아있는 성분들을 제거하기 위해 챔버를 고온으로 굽는 과정도 거치게 되며, 이를 통해 달 표면에서의 진공 정도에 해당하는 초고진공 상태를 만들어 낸다. 그리고 세슘을 가열하면 기체 상태의 세슘원자들이 상온에서 초속 수백미터의 속력으로 진공 챔버 안을 돌아다니게 된다. 문제는 세슘원자들이 맥스웰 볼츠만 분포를 따라 다양한 속력과 방향으로 움직인다는 것이다. 특수상대성이론에 따르면 다르게 움직이는 원자들의 고유시간들이 모두 다르게 되고, 따라서 원자들의 운동상태에 따라 공진주파수가 달라지게 된다. 정지해 있는 원자와 초속 수백미터로 움직이는 원자의 공진주파수는 수 GHz 이상 차이가 날 수 있다. 따라서 이들 원자들의 속력을 충분히 줄이고, 주파수를 조사할 수 있도록 한곳에 모을 수 있는 기술이 필요하다. 이를 위해 개발된 기술이 레이저와 자기장을 이용한 냉각 및 포획 기술(광자기 포획Magneto-optical trap)이며, 이를 개발한 분들은 그 독창성과 파급력을 인정받아 1997년 노벨물리학상을 수상하였다. 이렇게 냉각된 원자는 초속 cm 수준까지 속력이 줄어들고, 공간상의 한 점으로 모이게 되어, 주파수 측정을 위한 준비가 완료된다.
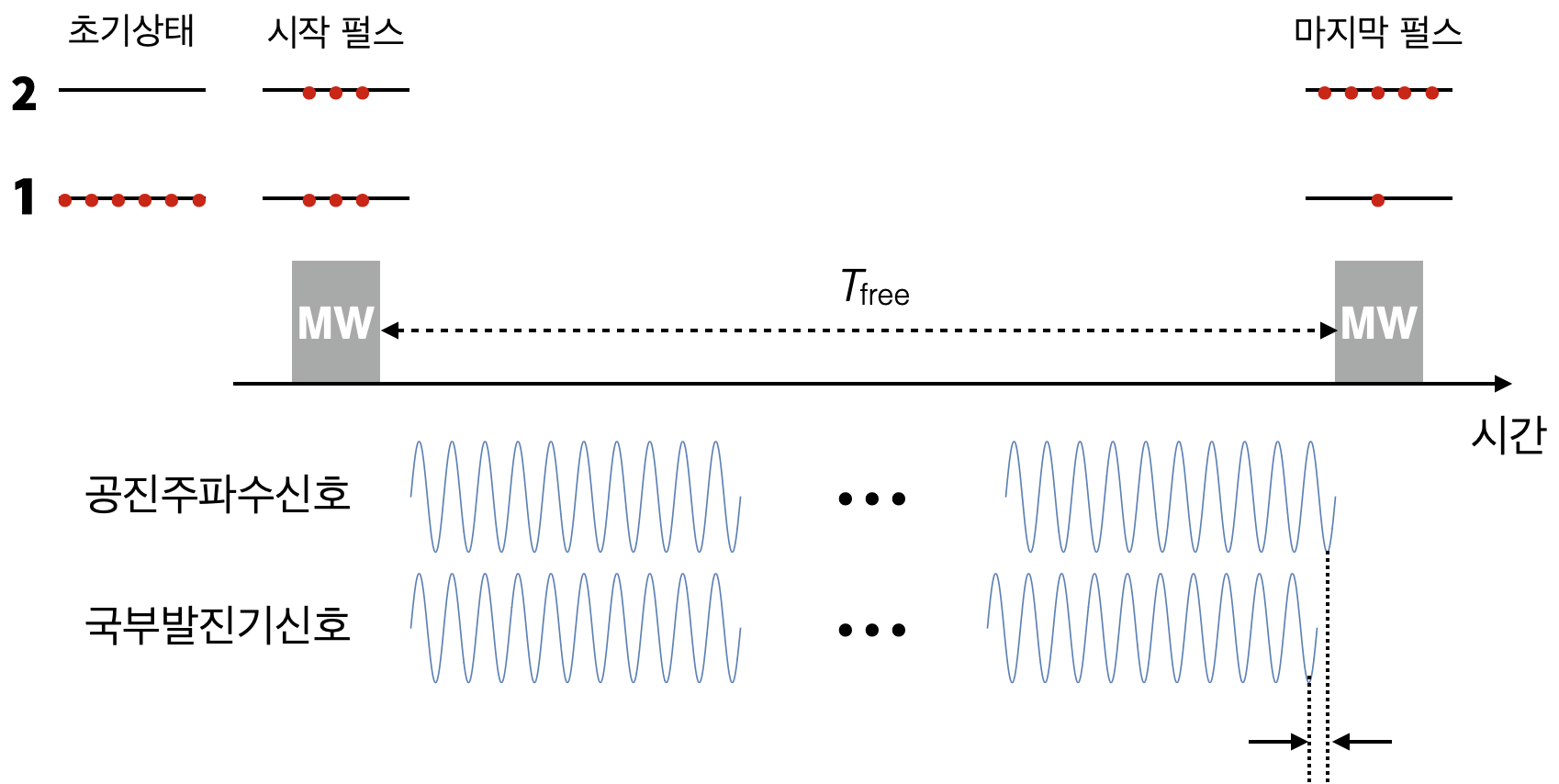
그리고 다음은 준비된 원자로부터 공진주파수를 정확하게 측정하는 방법을 알아보자. 먼저 위에서 모은 세슘 원자들의 전자들을 모두 [그림1]의 상태 1에 있도록 만든다. 그리고 국부발진기에서 만들어진 마이크로파 신호가 원자의 공진주파수와 정확하게 일치하면, 상태 1에 있던 모든 세슘 원자의 전자들이 2의 상태로 가게 되지만, 주파수가 공진주파수와 일치하지 않으면 일부의 전자만 2의 상태로 가게 되고, 일부 세슘원자들의 전자들은 1의 상태에 남아 있게 된다. 그렇다면 2의 상태에 올라간 원자의 개수를 어떻게 알 수 있을까? 2의 상태에 있는 전자들만 흡수하여 들뜬 상태로 갈 수 있는 주파수의 레이저([그림1]의 보라색 직선 화살표)를 조사하게 되면, 들뜬 상태로 전자들이 올라갔다가 자발 방출에 의해 다시 2의 상태로 오면서 빛을 내게 된다. 이 빛의 세기를 측정함으로써, 2의 상태에 있는 원자의 개수를 알 수 있고, 공진주파수와의 차이를 알 수 있게 된다. 만약 공진주파수와 국부발진기 주파수의 차이가 매우 작을 경우 이를 어떻게 알 수 있을까? 방법은 충분히 기다린 후 두 신호의 위상의 차이를 보면 알 수 있다. 이를 그네의 예를 들어 설명해 보자. 길이가 약간 다른 두 그네를 동시에 구르기 시작하면, 처음에는 같이 가는 것처럼 보일 수 있다. 하지만 오래 타다 보면 점점 두 그네의 움직임이 어긋나기 시작한다. 충분히 오래 그네를 탈수록 아주 작은 그네의 주기 차이를 알아낼 수 있다. 국부발진기 주파수의 미세한 차이를 알아내는 방법도 이와 유사하다. 위 [그림3]을 보자. 앞에서 설명한 바와 같이 처음에 모든 원자의 전자를 1의 상태로 준비한다. [그림3]의 맨 위에서 붉은색 원들이 각각의 원자들의 전자 상태를 나타낸다. 그리고 국부발진기로부터 마이크로파 신호를 펄스 형태로 원자에서 조사하여 절반 정도만 2의 상태로 가게 만든다. 그리고 Tfree 시간 동안 가만히 둔다. 국부발진기의 신호와 공진주파수가 다를 경우 둘 사이의 위상이 어긋나게 된다([그림3]의 아래 점선 사이의 간격). 그리고 시작 펄스와 같은 시간 동안 마지막 펄스를 원자에 조사한다. 최종적으로 전체 원자에서 상태 2에 있는 원자의 개수 비율이 국부발진기와 공진주파수의 차이를 보여준다. 100% 2의 상태에 있다면 공진주파수와 잘 일치하는 것이다. 앞서 설명한 바와 같이 Tfree가 길수록 주파수 차이를 더 정밀하게 알아낼 수 있다, 보통 상태 2에 원자가 거의 없게 될 때의 주파수 차이 \(\Delta f\)는 Tfree의 역수에 비례한다.
\(\Delta f \approx\)1/2Tfree
이렇게 주파수의 차이를 알아내는 방법으로, 이를 고안한 노먼 램지Norman F. Ramsey 교수는 1989년 노벨 물리학상을 받으셨다. 그리고 [그림3]과 같이 두 개의 서로 떨어진 펄스를 이용한 주파수 측정 방법을 “램지 조사Ramsey interrogation” 방법이라 하며, 원자시계 외에도 매우 다양한 곳에서 널리 사용되고 있다.
램지 조사 방법에 의하면 최대한 Tfree를 늘리는 것이 좋겠지만, 지구상에서는 원자를 가만히 놔두면 아래로 떨어지게 되어, 결국 관찰영역에서 원자들이 사라지게 된다. 그래서 고안된 장치가 원자분수시계atomic fountain clock이다. 말 그대로 원자를 분수fountain처럼 위로 던져서, 제자리로 돌아오는 동안의 걸리는 시간을 활용하는 것이다. 보통 분수 시계 장치에서는 돌아오는데 약 0.5초 정도 걸리게 되며, \(\Delta f\)는 위의 식을 따라 약 1 Hz가 된다. \(\Delta f\)는 2의 상태에 원자가 전혀 없을 때의 주파수 차이이기 때문에, 실제로는 공진주파수와의 차이가 더 작아도 이를 알 수 있으며, 보통 1 mHz 이하까지 차이를 알 수 있다. 원래 세슘주파수가 약 9 GHz이기 때문에 주파수 상댓값으로 계산하면 1 mHz/9 GHz \(\approx\) 10-13 이하까지, 차이를 알 수 있다(앞서 언급한 수소 메이저의 1초 안정도와 유사한 값이다). 그리고 여러 번 반복 측정하면, 정밀도를 더 높일 수 있어서 10-16 수준까지도 측정이 가능하다.
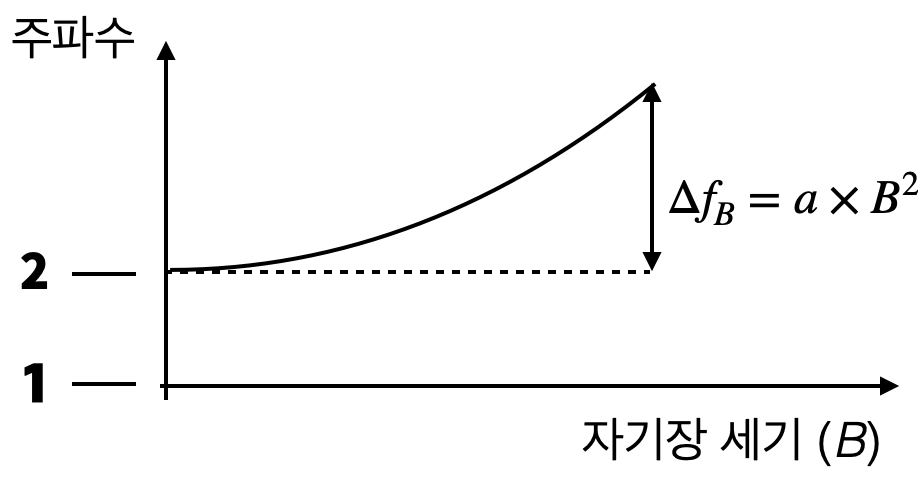
위의 설명은 원자의 공진주파수가 외부 환경에 의한 변화 혹은 “섭동”이 일어나지 않을 때를 가정한다. 하지만 실제 원자의 공진주파수는 여러 가지 원인에 의해 바뀔 수 있다. 가장 대표적인 경우가 자기장과 온도, 그리고 다른 원자와의 충돌 등에 의한 영향이다. 이를 제거하기 위해서는 먼저 외부 원인에 의해 공진주파수가 바뀌는 정도를 측정하거나 계산하여 관계식을 구한다. 그리고 시계가 동작하는 조건에서, 그 외부 원인을 최대한 정확하게 측정하고, 앞에서 얻은 관계식을 통해 외부 원인에 의해 주파수가 바뀌는 정도를 예측하여, 측정된 주파수를 보정한다. 예를 들어 아래 [그림4]와 같이 자기장에 의해 원자의 공진주파수가 바뀔 수 있다. 흔히 제만 효과로 불리는 이러한 변화를 보정하기 위해, 자기장의 세기 B의 변화에 따른 공진주파수의 변화 관계식 \(\Delta\)fB = a x B2 를 측정을 통해서 얻을 수 있다. 이렇게 얻은 관계식과, 실제 측정된 자기장의 값을 사용하여, 자기장에 의한 주파수 변화 효과를 제거할 수 있다. 관계식을 얻을 때 측정값을 사용하기 때문에 불확도가 있게 되고, 자기장 측정값에서도 불확도가 있을 수 있다. 현재의 기술로 도달할 수 있는 불확도는 10-16~10-17 수준이다. 이렇게 모든 환경 요인에 대한 공진주파수의 영향을 평가하여 불확도를 산정하는 과정을 “불확도 평가”라고 하며, 원자시계의 정확도를 결정짓는 가장 중요한 과정이고, 그래서 가장 큰 노력을 기울여야 하는 부분이다. 현재 전 세계적으로 운용되고 있는 분수 시계는 상대 주파수 불확도가 10-16 수준이며, 하루에 약 10 ps (1 ps=10-12 s) 틀리는 수준이다. 이러한 다수의 원자시계가 세계협정시UTC, Coordinated universal time를 생성하기 때문에, 세계협정시가 안정적으로 유지될 수 있다.
현재 세슘분수시계를 이용하여 구현된 시간의 잣대는 그 눈금의 불확도가 10-16 수준이다. 다시 말해 주파수 값을 17자리까지 정확하게 알 수 있다는 뜻이다. 이는 7개의 SI 기본 단위 중 최고의 정확도에 해당한다. 그래서 일찍이 노벨 물리학상 수상자인 아서 숄로Arthur Schawlow 교수는 주파수가 아니면 측정하지 말라Never measure anything but frequency고 까지 조언한 바가 있다. 하지만 정확한 시계의 여정은 여기서 멈추지 않았으며, 기존의 세슘원자기반 원자시계보다 100배 이상 정확도가 높은 시계들이 속속 등장하고 있다. 17자리보다 더 많은 자릿수가 필요하게 된 것이다.
광주파수 시계
앞서 기술한 세슘분수시계는 현재 초의 정의를 가장 정확하게 구현하는 원자시계이다. 하지만 현재 기술적인 한계에 다다랐으며, 불확도는 10-16수준에 머물러 있다. 더 높은 정확도를 얻기 위해서는 외부 환경 요인에 더 둔감한 에너지 층을 가진 원자를 사용하거나, 공진 주파수를 더 키우면 된다. 광주파수 시계(이하 “광시계”라 함)는 세슘의 공진주파수보다 1만배 이상 높은 광주파수 대역인 수백 THz(1 THz = 1012 Hz) 이상의 공진주파수를 가진 원자를 사용한다. 우리 나라에서는 한국표준과학연구원에서 이터븀이라는 원자를 사용하여 광시계를 개발하고 있다. 그 공진 주파수는 약 520 THz이다. 세슘시계와의 차이를 보기 위해, 원자시계가 1 Hz의 불확도를 가진다고 가정하자. 공진주파수가 9.2 GHz 라면 상대적인 주파수 불확도는 10-10이지만, 공진주파수가 500 THz라면 10-15수준이 되게 된다. 광주파수를 사용할 경우 더 정확하고 세밀한 눈금으로 주파수 변화를 읽을 수 있기 때문에, 정밀한 시계를 만들 수 있는 것이다.
우측 [그림5]에 묘사된 광시계의 구성은 [그림2]와 비슷하지만, MW가 아닌 눈에 보이는 빛의 주파수를 사용하기 때문에, 다른 요소들이 존재한다. 일단 국부발진기가 더 이상 MW나 RF 대역의 진동자가 아니라 레이저이다. 세슘원자분수시계의 경우와 마찬가지로 원자를 이용하여 연속적으로 주파수를 측정하기는 어렵기 때문에, 측정하지 않는 시간 동안 주파수가 안정적으로 유지될 수 있는 높은 안정도의 레이저를 제작하여 사용하게 된다. 보통 1초 동안의 상대 주파수 안정도가 10-15~10-17 수준으로 수소 메이저의 성능을 능가한다. 그리고 500 THz의 광주파수를 세거나 나눌 수 있는 전자장비가 없기 때문에, 광주파수로부터 1초를 만들기 위해 일명 “광주파수 빗optical frequency comb”이라는 장치를 사용한다. 이름에서 알 수 있듯이 광주파수 대역에서 빗과 같이 매우 일정한 간격의 레이저 모드가 존재하는 펄스 레이저이다. 보통 각 모드의 주파수는 매우 정확하게 알 수 있기 때문에, 국부발진기 레이저와 근처에 있는 모드 사이의 차이 값만 알면 광주파수를 정확하게 셀 수 있다.
그렇다면 이러한 광시계의 광주파수를 얼마나 정확하게 잴 수 있을까? 그것은 결국 눈금의 정확도에 달려 있다. 그리고 그 눈금은 현재로서는 세슘 원자의 공진주파수로 정해지며, 세슘분수시계로 구현된다. 현재 초의 정의에 따라 측정한 광시계의 주파수 값을 흔히 “절대주파수Absolute frequency”라고 부른다. 이터븀 원자의 경우 현재까지 측정된 값은 518,295,836,590,863.63(10) Hz이다. 마지막 괄호 안의 숫자는 불확도를 나타내는 숫자로서 0.10 Hz만큼 불확실하다는 뜻이며, 상대적인 비율로 따지면 2×10-16에 해당한다. 이는 [그림6]의 아래쪽 회색 눈금에서 표현된 것과 같이 세슘분수시계에 의해 결정되는 초의 불확도를 포함하고 있다. 세슘주파수와 이터븀 광주파수는 광주파수 빗에 의해 연결된다. 이에 반해 정확한 값은 모르더라도 이터븀의 실제 주파수 값으로부터의 불확도는 이보다 낮을 수 있다([그림6]의 위쪽의 회색 눈금으로 표현됨). 왜냐하면 이터븀 주파수로부터의 불확도를 추정할 때는 각종 외부 요인에 의한 영향을 측정 또는 이론적으로 예측하고, 외부요인을 실제 측정하여, 보정 값을 구하기 때문에, 절대 주파수의 불확도보다 낮아질 수 있다. 현재 가장 정확한 광시계는 약 1×10-18 수준으로 300억 년에 1초 틀리는 수준이다.
도대체 1×10-18 수준의 정확도로 무엇을 할 수 있을까? 2016년 정밀도가 커진 중력파 검출 장치 LIGO가 가동을 시작하고 얼마 지나지 않아 100년 전에 예측된 중력파가 관측되면서, 중력파 천문학이라는 새로운 학문을 연 것처럼, 극한 정확도의 광시계는 새로운 시공간 측정도구로서 활용되어, 지금까지 측정할 수 없었던 것을 측정할 수 있을 것으로 기대된다. 예를 들어 1×10-18 수준의 정확도를 가진 시계를 지구상에서 1cm만 들어 올려도, 일반 상대론에 의해 예측된 중력에 의한 시간의 빨라짐을 관측할 수 있다. 그뿐만 아니라 여러 물리상수가 원자의 공진주파수를 결정하는 데 기여하기 때문에, 여러 개의 정확도 높은 시계로 장기간 공진주파수를 관측하면, 변하지 않는 상수라고 생각되는 각종 물리상수들이 시간에 따라 변하는 것을 관측할 수 있을 것이라 기대하고 있다. 이제 광시계가 가져올 새로운 과학의 시대로 여러분을 초대한다.