수학과 물리학은 오랜 세월 동안 서로 큰 영향을 미치며 발전해온 두 기초학문입니다. 물리수학Physical Mathematics은 20세기 후반에 처음 등장한 학문으로, 수학과 물리학 사이의 새로이 밝혀진 관계를 연구하는 분야를 지칭합니다. 이 글에서는 최대한 기술적인 부분은 제외하고 단순한 예를 들어 이 신생 분야의 핵심 아이디어를 전달하는 것을 목표로 하겠습니다. 지면의 한계로 모든 내용을 충분히 다루지는 못하겠지만, 각주를 통해 HORIZON의 여러 훌륭한 글들을 추천하도록 하겠습니다.
1. 수학: 가장 오해받는 학문
수학과 물리학의 관계를 설명하기 위해서는 우선 수학과 물리학이 각각 어떤 학문인지부터 이야기해야 할 것 같습니다.1 먼저 수학이란 어떤 학문일까요? 독자 여러분들도 학창시절 10년 이상의 경험을 통해 각자 나름의 아이디어를 가지고 계실 것으로 생각합니다. 그러나 제가 주변의 직장인 친구들과 이야기를 나누어 본 것으로 미루어 짐작하건대, 아마 수학을 `공식을 외우고 주어진 문제를 풀기 위해 그 공식을 적용하는 법을 배우는 학문’이라고 생각하는 분들도 적지 않을 것 같습니다. 하지만 이는 수학자로서 몹시 억울한 오해이기에 이번 기회를 통해 수학에 대한 그 오해를 조금이라도 해소하고자 합니다.
다시 수학이 어떤 학문인지에 대한 질문으로 돌아와 보자면, 안타깝게도 수학자들 사이에서도 모두가 동의할 수 있는 정의는 없는 것 같습니다. 그래서 수학이 다른 자연과학과 사회과학의 학문분야와 차별화된 특징 둘을 짚어봄으로써, 수학에 대한 소개를 시작하고자 합니다.
첫째로, 수학이라는 학문 자체에는 궁극적인 목표가 없습니다. 반면에, 인간의 지성을 통해 정확하게 기술할 수 있는 것이라면 그 어떠한 것이라도 관심 대상이 될 수 있다는 특징이 있습니다. 그래서 자연환경 및 인간사회와 관련이 없어 보이는 추상적인 대상들도 수학의 연구 주제가 됩니다. 둘째로, 수학은 정의와 공리로부터 출발하여 증명을 통해 명제의 진위를 결정하는 특징을 가지고 있습니다. 여기서 정의와 공리는 약속된 시작점이고, 증명은 연역적인 방법으로 주어진 명제를 도출해내는 과정을 뜻하기에, 한 번 증명된 명제는 절대적인 의미에서 참이라는 것을 알 수 있습니다. 이 점은 자연과학과 사회과학의 이론이 실험, 관찰, 통계 등을 통해 귀납적으로 입증되는 것과 대비됩니다.
수학에 대한 추상적인 설명은 일단 이쯤 해두고 수학의 특징을 하나의 예를 들어 더 자세히 설명해 보겠습니다. 아마도 수학 전체에서 가장 중요하고 유명한 결과 중 하나인 피타고라스 정리는
직각삼각형의 세 변의 길이가 \(a,b,c\) 이고 변 \(c\)가 빗변일 때,
\(a^2+b^2=c^2\)이 성립한다
는 명제입니다.2 독자분들은 이미 이 정리에 익숙하여 대수롭지 않게 생각하실지도 모르겠습니다. 그러나 추상적인 대상에 대한 단 한 줄의 정리가, 언제 어디에서 그려진 삼각형이라도 한 각이 직각이라면 공통적으로 만족해야 하는 진리를 전한다는 사실은 곱씹어볼수록 놀랍고도 또 아름답게 다가옵니다.
이제 피타고라스 정리를 수학자의 눈으로(=호기심을 가지고) 살펴보고, 자연스럽게 떠오르는 질문 몇 개를 던져보며 수학자들이 내놓은 답도 함께 살펴보겠습니다.
• 아주 자연스러운 질문은 `피타고라스 정리를 직각삼각형이 아닌 일반적인 삼각형으로 일반화할 수 있는가’입니다.
임의의 삼각형이 주어져 있을 때,
세 변의 길이 사이의 관계를 구할 수 있는가?
이와 같은 질문에 정확한 답을 얻기 위해 수학자들은 `삼각함수’의 이론을 발전시켰으며, 주어진 질문에 대한 답은 `코사인 법칙’으로 주어집니다.
• 수학자들은 어떤 명제를 보았을 때 항상 `역은 성립하는가?’라는 질문을 합니다.
세 변의 길이가 \(a, b, c\)인 삼각형이 \(a^2 + b^2 = c^2\)를 만족할 때,
그 삼각형은 \(c\)를 빗변으로 가지는 직각삼각형인가?
이 질문의 답은 코사인 법칙에 의해 `그렇다’로 주어집니다.
• 간단한 직각삼각형의 예로서 \(a=1\)이고 \(b=1\)인 경우를 상상해 보겠습니다. 이러한 직각삼각형의 빗변 \(c\)는 \(c^2=2\)를 만족해야만 합니다.
\(c^2=2\)를 만족하는 \(c\)는 무엇인가?
이러한 질문은 정수의 비율로 나타낼 수 없는 `무리수’라는 개념을 이끌어냅니다. 유리수와 무리수는 합쳐서 `실수’를 이루고 이 개념은 후에 `미적분학’을 비롯한 `해석학’의 기초가 됩니다.
• 무리수의 길이를 가지는 변을 사용하지 않고 직각삼각형을 만들 수 있을까요?
방정식 \(a^2 + b^2 = c^2\)을 만족하는 자연수 세 쌍triple \((a,b,c)\)는
존재하는가? 존재한다면 얼마나 많은가?
이렇게 주어진 방정식 \(a^2 + b^2 = c^2\)을 만족하는 세 쌍을 `피타고라스 세 쌍Pythagorean Triple‘이라고 부릅니다. 예를 들어 \((3,4,5)\), \((5,12,13)\) 등이 예가 됩니다. 이는 반지름이 1인 원의 유리해와 일대일 대응하며, 따라서 무한히 많이 존재합니다.
• 이를 보다 일반화 해보겠습니다.
3 이상의 자연수 \(n\)에 대해서 \(a^n+ b^n=c^n\)을 만족하는
자연수 세 쌍 \((a,b,c)\)는 존재하는가?
이에 대한 답으로 17세기 수학자 페르마는 `존재하지 않는다’라고 주장했고, 이 명제가 바로 `페르마의 마지막 정리Fermat’s Last Theorem‘입니다. 이 명제는 이후 350여년간 여러 수학자들을 괴롭혔으나 1994년에 와일즈Andrew Wiles에 의해 증명되었습니다. 현대적인 관점에서 와일즈의 증명은 현대 수학의 중요한 가설인 랭글랜즈 프로그램Langlands Program의 추측 일부를 증명한 것으로도 볼 수 있습니다.3
• 보다 철학적으로
(직각)삼각형이란 무엇인가?
란 질문을 할 수도 있습니다. 이 질문은 사실 피타고라스 정리가 유클리드의 평행선 공리와 동치라는 점을 알고 나면 유클리드의 평행선 공리 자체에 대한 의문으로 볼 수도 있습니다. 실제로 구면 위에서 모든 각이 직각인 삼각형을 그리고 나서 보면 각 변의 길이 \(a,b,c\)가 서로 같기 때문에 이러한 삼각형에 대해서는 피타고라스의 정리가 성립하지 않습니다.
이렇듯 유클리드의 평행선 공리를 포기하고 얻는 새로운 종류의 기하학을 `비유클리드 기하학’이라 부릅니다.4
• 피타고라스 정리는 빗변의 길이를 다른 두 변의 길이를 통해 알아내는 방법으로 생각할 수도 있습니다. 이 관점에서는 다음과 같은 질문이 자연스럽습니다.
일반적인 곡선의 길이는 어떻게 구할 수 있을까?
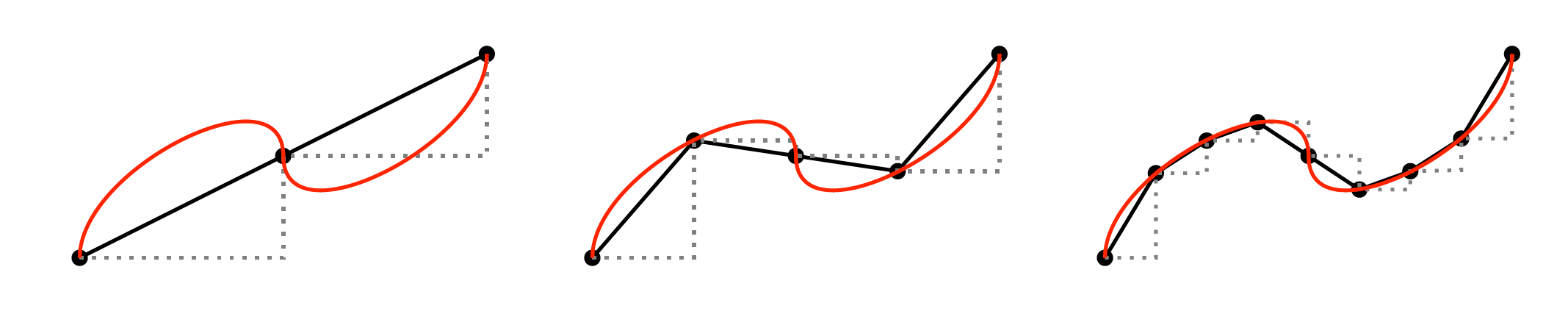
여기에 대한 답을 찾기 위해 다음 그림을 생각해 봅시다.
이 그림에서 곡선을 더욱 잘개 쪼개는 것을 상상해 본다면, 일반적인 곡선의 길이를 무한히 많은 선분의 길이의 합으로 얻어낼 수 있습니다. 여기서 이 선분을 직각삼각형의 빗변으로 생각하여 피타고라스 정리를 적용한다면, 일반적인 곡선의 길이를 각 선분들의 가로세로 방향의 변위를 통해 알아낼 수 있습니다. 이 아이디어를 일반화함으로써, 비유클리드 기하학에서 다루는 거리공간까지 포함하는 개념인 다양체Manifold에 대한 이론체계를 이끌어 낼 수 있습니다. 이러한 대상을 연구하는 분야는 리만기하학Riemannian Geometry이라 불립니다.5
다시 한번 수학이 어떤 학문인지에 대해 정리해보도록 하겠습니다. 이 글에서 우리는 추상적 대상에 대한 절대적 진리인 피타고라스 정리를 시작점으로 삼고, 호기심을 갖고 추상화와 일반화를 사용하여 자유롭게 질문하며, 엄밀한 방법론을 통해 정확히 답을 찾으려는 노력을 하였습니다. 이를 통해 보편적이며 절대적인 여러 새로운 진리에 다다를 수 있었습니다. 이제 이렇게 얻은 각각의 진리에 대해서도 마찬가지로 자유롭게 질문을 하고 정확히 답을 찾으려 할 수 있습니다.6 더 나아가 피타고라스 정리와 다른 시작점 또한 수백, 수천 개가 더 존재하고, 각각의 시작점으로부터 뻗어나가 자유롭게 질문을 하고 그에 대한 답을 하는 것 역시 수학의 연구주제가 되겠습니다. 이렇게 다르게 보이는 시작점을 가지고 출발한 수학적 진리들은 신기하게도 때때로 서로 얽히고설킨 구조를 가집니다. 이러한 수학적 진리 사이의 미처 짐작하지 못했던 연관성을 공부하는 것 또한 수학연구의 핵심적인 부분입니다.
2. 물리학과 수리물리학: 자연과학에서 수학의 말도 안되는 효용성
물리학이란 어떤 학문일까요? 물리학은 물질, 힘, 에너지, 운동, 시공간과 같은 개념을 연구하여 우리 우주가 작동하는 근본 원리를 이해하는 것을 주 목표로 하는 학문입니다. 그렇다면 호기심을 좇아 추상적 대상을 탐구하는 수학과 우리 우주의 근본 원리를 이해하려는 물리학은 어떤 관계가 있을까요? 역사적으로 보았을 때 두 학문은 뗄 수 없는 밀접한 관련이 있습니다. 먼저 수학의 입장에서 볼 때, 물리학은 정수의 성질에 대한 연구분야인 정수론과 도형과 공간에 대한 연구분야인 기하학과 함께 수학적 활동의 주요 원천이었습니다. 또한 물리학의 입장에서는 우주의 근본 원리를 정량적으로 기술하는 언어로서 수학이 필수적이었습니다. 이러한 밀접한 관계를 더욱 명확히 설명하기 위해 몇 가지 물리학의 핵심 이론과 그에 해당하는 수학 분야의 예를 들어보겠습니다.
• 고전역학Classical Mechanics은 거시적인 물체에 작용하는 힘과 운동 사이의 관계를 연구하는 분야입니다. 뉴턴Sir Isaac Newton은 (라이프니츠Gottfried Wilhelm Leibniz와 독립적으로) 미적분학Calculus을 발전시켜 고전역학의 운동 법칙과 만유인력의 법칙을 기술했습니다.7
• 전자기학Electromagnetism은 전기Electricity와 자기Magnetism가 만들어내는 현상들을 연구하는 분야입니다. 맥스웰James Clerk Maxwell은 이전에 알려져 있던 전기와 자기 이론들을 통합하여, 이러한 현상들을 전기장Electric Field과 자기장Magnetic Field이 만족시켜야 하는 단 네 개의 편미분방정식Partial Differential Equation; PDE으로 기술하였습니다.8
• 상대성 이론Theory of Relativity은 시공간의 성질에 대한 이론입니다. 아인슈타인Albert Einstein의 일반 상대성 이론은 중력의 본질을 시공간의 휘어짐으로 설명했습니다. 이러한 물리적 아이디어를 정확히 기술하기 위해, 앞서 피타고라스 정리로부터 출발해서 순전히 호기심을 통해 다다랐던 리만기하학Riemannian Geometry과 리만기하학의 변주가 반드시 필요했습니다.9
• 양자역학Quantum Mechanics은 고전역학이 통하지 않는 미시적인 세계의 현상을 연구하는 분야입니다. 보어Niels Bohr, 슈뢰딩거Erwin Schrödinger, 하이젠베르크Werner Heisenberg, 보른Max Born, 디랙Paul Dirac 등의 물리학자들은 선형대수학Linear Algebra, 군론Group Theory, 그리고 미분방정식Differential Equation 등의 수학적 언어를 사용하여 미시세계에서 나타나는 물리적 현상의 불연속성과 확률적 특성에 대해 이해하고 이들을 정량적으로 기술하는 이론을 발전시켰습니다.10
위에서 보듯, 대부분의 경우 물리학에 필요한 수학 분야는 이미 수학 자체로서 발전되었으며, 물리학자들은 이러한 수학을 사용하여 물리학의 아이디어를 명확하게 기술할 수 있었습니다. 추상적인 대상에 대한 호기심에서 발전된 학문이 우주의 원리를 기술하는 올바른 언어로 사용된다는 사실은 매우 놀라운 일입니다. 물리학자 위그너Eugene Wigner는 이러한 사실을 강조하여
자연과학에서 수학의 말도 안되는 효용성
The Unreasonable Effectiveness of Mathematics in the Natural Sciences
이라고 말하기도 했습니다.
수학과 물리학의 관계는 여기서 그치지 않았습니다. 바로 이러한 관계가 두 분야 모두를 더욱 발전시켰던 것입니다. 물리학이 수학을 도와준 예를 먼저 들어보겠습니다. 디랙Paul Dirac은 양자역학에 사용하기 위해 당시까지 수학적으로 정의되지 않았던 더 일반적인 함수를 도입했습니다. 이는 슈바르츠Laurent Schwartz가 분포Distribution의 이론을 발전시키는 계기가 되었습니다.11분포의 이론은 이후 수학 전반에서 매우 중요하게 활용되고 있습니다. 또한, 수학이 물리학을 도와준 반대의 경우를 살펴보면, 상대성 이론의 아인슈타인 방정식Einstein Field Equations을 수학적으로 연구함으로써 블랙홀의 존재를 예측하고, 상대론적 양자역학의 디랙 방정식Dirac Equation을 통해 반물질Antimatter의 존재도 예측할 수 있었습니다.12 이러한 예측들은 이후 실험적으로 확인되어 우리 우주를 이해하는 데 필수적인 요소가 되었습니다.
이처럼 물리학의 개념을 이해하거나 물리학의 문제를 해결하기 위해 필요한 수학적 방법론을 발전시키고, 또 수학 이론을 응용하고 적용하여 물리학의 새로운 결과를 찾는 분야를 수리물리학Mathematical Physics이라고 합니다.
이제 수리물리학의 성배에 대해 설명드리며 수리물리학에 대한 소개를 마무리하려 합니다. 양자역학은 미시세계의 입자(=파동)를 기술하는 물리 이론입니다. 반면에 전자기학에서는 전기장과 자기장과 같은 장의 개념을 고전역학적으로 다룹니다. 입자와 장은 서로 영향을 미치기 때문에 궁극적으로 우주를 기술하는 이론은 장의 개념 또한 양자역학적으로 다룰 수 있어야 합니다. 이를 성공적으로 기술한 이론체계를 양자장론Quantum Field Theory이라고 하는데, 이는 현재까지 우리 우주의 작동 원리를 설명하는 데에 있어 가장 완결성이 있는 체계입니다. 그 중에서도 특히 표준 모형Standard Model은 가장 성공적인 양자장론의 예시로, 중력을 제외한 모든 힘과 모든 미시입자들을 정밀하게 기술하는 데에 성공했습니다.13
실제 물리량을 기술하는 데에 있어 양자장론에서 가장 중요한 양은 상관 함수Correlation Function로 다음과 같은 형태로 표현됩니다.
\(\langle O_1, \cdots, O_n\rangle = \int_{\phi \in \mathcal F(M)} O_1(\phi)\cdots O_n(\phi) e^{iS(\phi) } d \phi \)
각 표기법에 대한 자세한 설명은 생략하겠습니다. 만약 \(\mathcal F(M)\)이 실수들의 공간으로 주어진다면 이 적분은 미적분학에서 다루는 적분의 형태인 \(\int_{-\infty}^\infty O_1(x)\cdots O_n(x) e^{iS(x)} dx\) 꼴이 됩니다. 흥미로운 점은 일반적으로 \(\mathcal F(M)\)이 무한차원이어서 적분이 수학적으로 잘 정의되지 않는다는 것입니다. 그러나 물리학자들은 이러한 표현으로부터 유한한 값을 얻어내는 방법을 고안해냈고, 이렇게 얻은 값들은 알려진 거의 모든 실험 결과를 오차 범위 내에서 설명할 수 있습니다. 이는 수학자의 입장에서는 믿기 어려운 일입니다. 정의도 되지 않는데 유한한 값을 내놓을 수 있고, 또 그 값이 실제로 물리적인 의미를 가진다니요! 이로 인해 생기는 수리물리학의 가장 핵심적인 과제는 양자장론을 이해하기 위해 필요한 수학적 방법론을 발전시키는 것입니다.14 이를 해결하는 데 성공한다면 분명 물리학에도 새로운 결과를 내놓을 것으로 보입니다.
3. 물리수학: 수학에서 물리학의 말도 안되는 효용성
20세기 후반에 들어서 수학과 물리학 사이의 관계에 새로운 혁명이 일어났습니다. 바로 우리 우주를 기술하기 위해 발전시킨 물리학의 이론이 그와 전혀 상관 없어 보이는 순수수학의 문제를 해결하는 데 쓰일 수 있다는 점입니다. 이러한 관찰로부터 물리수학Physical Mathematics이라 불리는 학문이 탄생하게 되었습니다. 수리물리학의 전제와 완벽히 대조되는 점을 강조해보자면, 물리수학은
수학에서 물리학의 말도 안되는 효용성
The Unreasonable Effectiveness of Physics in the Mathematical Sciences
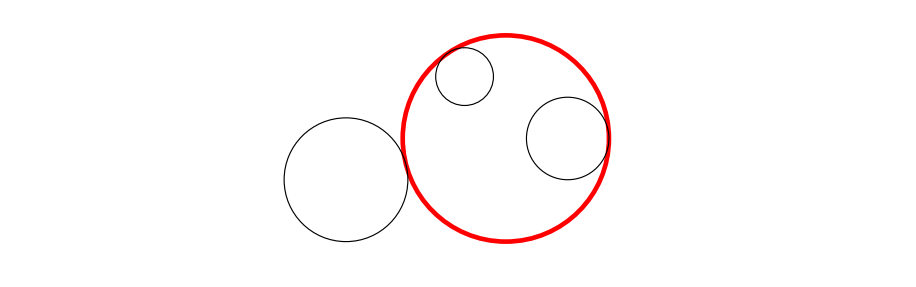
을 찾는 학문이라 할 수도 있겠습니다. 하나의 예를 들어 더 자세히 설명해 보도록 하겠습니다. 열거 기하학Enumerative Geometry은 주어진 조건을 만족하는 기하학적 대상의 개수를 세는 분야입니다.15 예를 들어, `평면 상에 주어진 서로 다른 두 점을 지나는 직선은 몇 개인가?’라는 질문에 대한 답이 `1’임은 명백합니다. 더 흥미로운 질문으로 그리스 수학자 아폴로니우스Apollonius of Perga가 기원전 200년경 제시했던 `평면 상에 주어진 세 원에 모두 접하는 원은 몇 개인가?’가 있습니다.
아폴로니우스는 이 문제에 대해 `일반적으로 주어진 세 원에 모두 접하는 원은 항상 8개 존재한다’라는 답도 함께 내놓았습니다.
이 분야에서 역사적으로 중요한 질문은 `일반적Generic 5차 3차원 복소다양체Quintic Threefold에 살고 있는 차수가 \(d\)인 유리 곡선Rational Curve은 몇 개인가?’입니다.16 여기서 \(d\)는 1 이상의 정수로서, \(d\)가 증가함에 따라 문제가 매우 어려워집니다. 실제로 \(d=1\)인 경우에는 슈베르트Hermann Schubert가 1886년에 슈베르트 계산법Schubert Calculus을 통해 \(n_1=2875\)임을 발견했지만,17 그 다음 경우인 \(d=2\)는 100여년 후인 1986년에야 당대 최신의 대수기하학의 언어를 사용하여 \(n_2=609250\)임을 알아냈습니다. 이후 노르웨이의 수학자 그룹이 1991년에 컴퓨터를 사용하여 \(n_3=317206375\)를 계산했습니다.
여기서 하나의 반전이 있습니다. 바로 1991년, 물리학자 그룹이 모든 \(d\)에 대한 \(n_d\)를 한꺼번에 발표했다는 점입니다! 사실 학회에서 만난 수학자들과 물리학자들은 원래 \(n_3\)에 대해 서로 다른 답을 주장했습니다. 물리학자들이 양자장론의 아이디어를 사용했고 수학적으로 잘 정의되지 않은 방법으로 계산했다는 것을 알고 있던 수학자들은, 당연히 물리학자들이 어딘가에서 실수를 했을 것이라고 믿어 의심치 않았습니다. 그러나 노르웨이 수학자들은 불과 채 3달이 지나지 않아 그들이 사용한 컴퓨터 프로그램의 에러를 찾아냈고, 이를 수정한 결과 물리학자들과 같은 답을 찾아냈습니다. 그 결과가 바로 위에서 언급한 \(n_3=317206375\)입니다. 또한 이미 `답’을 알게 된 수학자들은 오래 지나지 않아 1996년에 물리학자들이 예견했던 \(n_d\)가 모두 옳다는 것을 증명할 수 있었습니다.18
독자 여러분들도 이 당시 열거 기하학을 연구하던 수학자들이 얼마나 큰 충격을 받았을지 상상해보기 바랍니다. 추상화와 일반화의 대가인 수학자들이, 그들의 본토인 순수수학의 주요 문제에서, 물리학자들에게 \(2:\infty\)로(컴퓨터 탓을 한다면 \(3:\infty\)으로) 진 꼴입니다. 도대체 어떻게 이런 일이 가능했을까요? 물리학자들이 흑마법이라도 배운 것일까요? 그렇습니다. 이 흑마법의 이름은 바로 물리학의 쌍대성Duality입니다. 물리학자들이 열거 기하학의 문제를 공략한 비법을 간단하게 요약해 보겠습니다.
(A) 칼라비–야우 3차원 다양체Calabi–Yau Threefold \(X\)가 있을 때마다 특정한 양자장론 두 개를 건설할 수 있습니다.19 여기서 \(X\)의 예로는 앞서 살펴보았던 5차 3차원 복소다양체Quintic Threefold를 사용할 수 있습니다. 편의상 이렇게 만들어진 양자장론을 \(\mathcal{T}(X,\text{A})\)와 \(\mathcal{T}(X,\text{B})\)라고 부르겠습니다.
(B) 5차 3차원 복소다양체 \(X\)에 대해 \(n_d=n_d(X)\)를 구하는 열거 기하학의 문제는 양자장론 \(\mathcal{T}(X,\text{A})\)의 상관 함수Correlation Function를 구하는 문제와 동일합니다.
(C) 칼라비–야우 3차원 다양체 \(X\)가 있을 때 그와 쌍대Dual 관계를 가지는 칼라비–야우 3차원 다양체 \(X^\vee\)이 존재합니다. 이는 양자장론 \(\mathcal{T}(X,\text{A})\)와 양자장론 \(\mathcal{T}(X^\vee ,\text{B}) \)는 서로 다르게 생겼더라도, 그들의 상관 함수는 같아야만 한다는 주장입니다. 이런 상황에서 \(X^\vee\)는 \(X\)의 거울 다양체Mirror Manifold로 불립니다.20
(D) 양자장론 \(\mathcal{T}(X^\vee ,\text{B})\)의 상관 함수는 특정한 종류의 적분으로 계산 가능합니다. 이 적분의 계산은 열거 기하학의 계산보다 비교적 쉽게 할 수 있습니다.
(E) 두 양자장론 \(\mathcal{T}(X,\text{A})\)와 \(\mathcal{T}(X^\vee ,\text{B})\)의 상관 함수가 동일해야 하므로, 우리가 궁금했던 숫자인 \(n_d=n_d(X)\)가 \(\mathcal{T}(X^\vee ,\text{B})\)의 상관 함수로 주어진다고 추측합니다.
이처럼 다양체 \(X\)에 대한 정보를 이와 다른 공간 \(X^\vee\)의 정보를 통해 얻어내는 이론을 거울 대칭Mirror Symmetry 이론이라고 합니다. 앞서 설명했듯이 이러한 물리학자들의 사고과정은 수학적으로 잘 정의되지 않았음에도 불구하고 결과적으로 무한히 많은 경우에 대해 옳은 답을 주었습니다. 당연하게도 여러 수학자들은 이렇게 순수수학의 방법론을 사용하지 않고도 수학적 진리를 얻어내는 흑마법의 비밀에 큰 관심을 가지게 되었습니다. 이처럼 1991년에 시작된 거울 대칭 이론은 그 후로 여러 순수수학의 연구 방향을 완전히 바꾸며, 그 자체로 새로운 수학 분야로 자리잡게 됩니다.
거울 대칭 이론은 물리수학 분야의 단 하나의 예에 불과합니다. 보다 일반적인 물리수학의 연구는 다음과 같은 단계를 따른다고 볼 수 있습니다.
① 순수수학에서 다루고 있었던 문제의 물리적인 문맥을 찾습니다. 거울 대칭 이론의 예에서는 (A), (B)에 해당합니다.
② 이렇게 찾은 문맥에서 존재하는 물리학의 흑마법을 사용함으로써 물리적인 결과를 얻습니다. 거울 대칭 이론의 예에서는 (C)에 해당합니다.
③ 물리학의 결과를 다시 수학으로 옮깁니다. 거울 대칭 이론의 예에서는 (D), (E)에 해당합니다.
앞서 보았듯이 거울 대칭 이론에서는 이를 통해 이전의 순수수학적인 방법으로는 상상도 할 수 없었던 새로운 추측을 얻었습니다.
또다른 예인 4차원 매끈한 다양체Smooth Manifold 이론에서 물리수학의 역할 또한 간단히 살펴보겠습니다. 기하학과 위상수학에서 \(n\)차원 다양체가 언제 같고 다른지에 대해 답하는 분류Classification 문제는 가장 중요한 문제 중 하나로 여겨집니다. 1차원과 2차원 다양체의 분류는 19세기부터 알려져 있었습니다. 3차원 다양체의 분류는 페렐만Grigori Perelman이 서스턴William Thurston의 기하화 추측Geometrization Conjecture과 푸앵카레 추측Poincaré Conjecture을 해결함으로써 큰 진전을 이루었습니다.21 만약 4차원 이상이라면 문제가 훨씬 어려울 것 같지만, 놀랍게도 단일 연결Simply Connected인 5차원 이상의 다양체는 분류가 가능하다는 것이 알려져 있습니다.
하지만 4차원은, 3차원과 같은 기하화 추측도 존재하지 않고 5차원 이상에서 통하는 일반적 이론도 사용할 수 없어 가장 어려운 차원으로 여겨집니다. 주어진 다양체들이 다르다는 것을 증명하기 위한 가장 효과적인 방법은 불변량Invariant을 건설하고 계산하는 것인데, 4차원 매끈한 다양체는 그조차 몹시 어려웠습니다. 이러한 상황에서 도널드슨Simon Donaldson은 고전역학적인 게이지 이론Gauge Theory의 아이디어를 사용해서 도널드슨 불변량Donaldson Invariant을 도입했고, 이는 4차원 매끈한 다양체 이론의 시작을 알렸습니다. 하지만 도널드슨 불변량의 계산은 굉장히 어려웠으므로 이를 이용해 분야의 큰 진전을 이루는 것 또한 힘들었습니다. 이 때 물리학자 위튼은 다음과 같은 물리수학의 아이디어를 통해 훨씬 효과적인 불변량을 도입했습니다.
① 4차원 매끈한 다양체의 도널드슨 불변량의 물리적 문맥을 4차원 비가환Non-abelian 위상 양자장론에서 찾습니다.
② 4차원 초대칭 양자장론Supersymmetric Quantum Field Theory의 사이버그–위튼 이론Seiberg–Witten Theory이라는 흑마법은, 비가환 양자장론이 그보다 훨씬 단순한 가환Abelian 양자장론과 같다는 결론을 줍니다.22
③ 가환 위상 양자장론의 상관 함수를 계산함으로써, 도널드슨 불변량과 같은 양의 정보를 가지면서도 훨씬 다루기 간단한 사이버그–위튼 불변량Seiberg–Witten Invariant을 건설합니다.23
이렇게 새로 도입된 불변량은 역시나 이전의 수학으로는 상상도 할 수 없었던 대상이며, 수학자들은 이를 이용해 4차원 매끈한 다양체 이론에서 수많은 혁명적인 결과들을 얻을 수 있었습니다.
최근에는 랭글랜즈 프로그램Langlands Program의 대수기하학적인 형태인 기하학적 랭글랜즈 프로그램Geometric Langlands Program에서도 물리수학의 아이디어를 통해 새로운 추측을 내놓고, 새로운 대상을 건설하고, 새로운 구조를 발견하며, 또 새로운 정리를 증명할 수 있었습니다.
4. 결론
수학과 물리학은 그 목적과 방법론 면에서 몹시 다른 두 기초학문입니다. 수학은 호기심을 바탕으로 추상적인 대상에 대해 질문을 하고 그에 대한 정확한 답을 추구하는 학문이며, 물리학은 우주의 근본 원리를 이해하려는 학문입니다. 놀랍게도 물리학을 기술하는 언어로서 수학은 말도 안되는 효용성을 보였습니다. 이러한 관계는 수학과 물리학 각각의 발전에도 큰 도움이 되었습니다.
20세기 후반에는 더욱 놀랍게도 물리학의 아이디어를 통해 순수수학의 여러 분야에 혁신적인 결과를 낼 수 있다는 사실이 드러났습니다. 이렇게 새로이 밝혀진 수학과 물리학 사이의 관계를 탐구하는 분야가 바로 물리수학입니다. 물리수학은 다양한 수학 분야에 새로운 시각과 맥락을 제공하며 순수수학의 연구 방향을 더욱 풍부하게 만들었습니다. 앞으로도 물리수학의 영향력은 계속 확장될 것으로 기대됩니다.