2025년 아벨상 수상자 마사키 카시와라

 

 

 

2025년 아벨상은 일본 교토대학교의 수학자 마사키 카사와라 (Masaki Kashiwara)에게 수여되었습니다. 공식 발표문에 기재된 수상 사유는 다음과 같습니다[1]. 

“for his fundamental contributions to algebraic analysis and representation theory, in particular the development of the theory of D-modules and the discovery of crystal graphs.” 

 

 

주요 업적으로 언급된 \(D\)-모듈 이론^{\(D\)-module theory}과 결정기저 이론^{crystal bases theory}은 대수적 해석학과 표현론에서 중요한 위치를 차지하고 있는 이론으로 \(D\)-모듈 이론은 해석학과 대수학을 그리고 결정기저 이론은 표현론과 조합론을 연결합니다. 카시와라의 대표업적에 관한 구체적인 공헌 내용은 노르웨이 한림원의 홈페이지에 잘 나와있는 관계로 본 글에서는 대표업적으로 언급된 \(D\)-모듈과 결정기저에 초점을 맞추어 살펴보려고 합니다. 카시와라의 전기와 연도별 업적, 그리고 함께한 동료들에 대한 부분은 노르웨이 한림원의 공식 카시와라 전기 [2]를 살펴봐 주시면 좋을 것 같습니다. 그러면 \(D\)-모듈과 결정기저의 바탕을 이루는 모듈^module에 대한 개념에 대해서 먼저 이야기 하겠습니다.

 

 

대수^algebra는 스칼라 위에 덧셈과 곱셈이 있는 대수적 대상을 말합니다. 스칼라는 실수^{real number}와 같은 대수적 대상인 체^field를 의미하고, 실수 위의 \(2\times 2\) 행렬들의 집합이 대수의 대표적인 예가 됩니다. 여기서 행렬 합과 행렬 곱이 대수의 덧셈과 곱셈이 되지요. 수학에서 자연스럽게 등장하는 대수들은 그 구조가 매우 복잡할 수 있습니다. 연산의 구조가 매우 복잡해서 그 자체로는 잘 이해하기 힘들 때가 있지요. 이럴 때는 대수 그 자체를 보기 보다는 그것이 작용하는 좀 더 간단한 공간(수학적으로는 벡터공간^{vector space})을 대신해서 살펴보면 도움이 됩니다. 작용된 하나의 공간은 대수의 구조 중 일부의 정보만 담고 있지만, 작용된 여러 공간들을 함께 살펴보면 퍼즐조각 맞추듯 복잡한 대수의 구조를 유추할 수 있습니다. 이렇게 대수가 작용하는 공간을 대수가 \(‘표현된’\) 공간이라 해서 주어진 대수의 표현^{representation} 혹은 모듈 ^module이라고 부릅니다. 만약 주어진 대수 \(R\)이 체^field라면, 예를 들어 실수 혹은 복소수라면, 이 대수 \(R\)의 모듈은 일반적인 벡터공간이 됩니다. 따라서 작용 관점에서 모듈은 벡터공간의 일반화로 이해할 수 있고, 벡터공간의 구조에 스칼라 곱이 있는 것과 마찬가지로 모듈의 구조에는 대수 \(R\)의 작용이 있다고 이해할 수 있습니다. 

 

이러한 모듈들의 성질과 구조를 살펴보는 이론을 표현론^{representation theory}이라 부릅니다. 표현론은 대수학의 중요한 연구분야 중 하나로 표현론 그 자체로 중요한 의미를 가지지만, 기하학과 수리물리학을 포함한 다양한 영역에서도 자연스럽게 등장합니다. 큰 관점에서 보면 모듈은 대칭성이 투영된 공간을 의미하므로 다른 영역에서 중요하게 다루는 대칭성들이 투영된 공간은 표현론의 입장에서는 자연스럽게 모듈로 이해할 수 있습니다. 이러한 이유로 표현론은 다른 수학적 영역과의 접점이 많은 연구분야입니다. 

 

 

 

\(D\)-모듈 이론은  미분 연산자를 대수적으로 연구하고 이해하는 수학적 도구입니다. 카시와라는 이 연구 분야를 확립하고 혁신적으로 발전시킨 연구자입니다. 힐베르트의 21번째 문제로 부터 나온 리만–힐베르트 대응^{Riemann–Hilbert correspondence}의 일반화와 카즈단-루스틱 추측^{Kazhdan–Lusztig conjecture}의 증명을 포함한 카시와라의 학문적 기여는 공식 카시와라 전기 [2] 와 호타^{Ryoshi Hotta}, 타케우치^{Kiyoshi Takeuchi}, 그리고 타니사키^{Toshiyuki Tanisaki}의 \(D\)-모듈에 관한 책 [3] 의 서문을 참조하시면 좋을 듯 합니다.

 

\(D\)-모듈은 \(D\)와 모듈^module의 합쳐 놓은 단어로 \(D\)는 해석학에서 중요한 개념인 미분^differential을 나타냅니다. 따라서 \(D\)-모듈은 이름 그 자체로부터 해석학과 대수학의 교집합 영역에 속한다는 것을 알 수 있습니다.  \(D\)-모듈을 이야기하기 위해서는 \(D\)에 연관된 대수가 등장해야 합니다. 그 대수는 주어진 다양체 \(X\) 위에 작용하는 모든 미분 연산자^{differential operator}들과 다양체 위의 정칙함수의 곱셈들로 생성된 대수 (정확하게는 다발^sheaf로 이해해야 하지만)로 보통 \(\mathcal{D}_X\)로 표시합니다. 예를 들어 \(X\)를 복소수들의 집합 \(\mathbb{C}\)라 하면 대표적인 정칙함수 \(f(z)=z\)와 미분 연산자 \(d \over d z\)를 생각할 수 있습니다. 주어진 함수 \(g(z)\)에 대하여, 함수 \(g(z)\)를 곱하는 것은 자연스럽게 함수들로 구성된 대수의 작용자로 이해할 수 있습니다. 따라서 함수들의 곱셈과 미분 연산자의 곱 규칙 때문에 

\(\frac{d}{d z}  \cdot z = z \cdot   \frac{d}{d z} + 1\)

라는 자명하지 않은 관계가 미분연산자 대수 \(\mathcal{D}_X\) 안에서 생기게 됩니다. 그러므로 가장 간단한 다양체인 \(\mathbb{C}\)에 대해서도 그것의 \(\mathcal{D}_X\)는 자명하지 않은 대수가 됩니다. 일반적으로 다양체가 복잡해지면 그것의 미분연산자 대수의 구조도 복잡해지고 어려워집니다. 

 

이제 \(D\)-모듈을 이야기할 수 있습니다. \(D\)-모듈은 미분연산자의 대수 \(\mathcal{D}_X\)의 모듈을 의미합니다. 따라서 \(D\)-모듈은 개념적으로 해석적 대상인 미분 연산자의 이야기를 대수적 대상인 모듈의 이야기로 건너갈 수 있는 수학적 연결을 만들어 주고 여러 대수적인 도구들을 해석적 대상에 적용시킬 수 있는 장치를 마련해 줍니다. 예를 들어 다음의 수학적 상황을 생각해 봅시다. 미분방정식 \(\frac{df(z)}{dz} = f(z) \)의 풀이는 해석적 영역에서 중요한 질문입니다(이 질문의 답은 지수함수 \( C e^z\) (단, \(C\)는 상수) 이지요). 이 방정식은 미분 연산자의 입장에서 \((\frac{d}{dz} – 1 )f(z)=0 \)로 쉽게 바꿀 수 있습니다. 따라서 이것은 연산자 \(\frac{d}{dz} – 1\)를 적용했을 때 0이 되는 함수이고, 이를 좀 더 대수적으로 말하면 연산자 \(\frac{d}{dz} – 1\)의 핵^kernel에 속하는 함수라 말할 수 있고, 좀 더 나아가 몫으로 정의된 \(D\)-모듈 \(\mathcal{D}_X / \mathcal{D}_X (\frac{d}{dz} – 1)\)을 생각하면 여핵^cokenel입장에서 자연스럽게 처음의 미분방정식과 연결됩니다. 따라서 해석적 대상인 미분방정식을 \(D\)-모듈의 영역으로 끌어들여 대수적 입장에서 이해할 수 있습니다. 이런 식으로 미분 연산자로 작성된 해석적 문제를 연산자에 연관된 대수적 대상으로 바꾸어 분석하고 이해하는 것이 \(D\)-모듈 이론의 핵심적인 부분이라 하겠습니다.    

 

 

 

결정 기저^{crystal bases}는 양자군의 표현론에서 등장하는 개념으로 양자군 혹은 그것의 모듈의 대수적 구조를 잘 드러내는 조합적 대상으로 이해할 수 있습니다. 결정기저의 존재성과 풍부한 성질들은 카시와라에 의해서 발견되고 정립되었습니다. 결정기저에 대한 카시와라의 학문적 업적과 관련 이야기는 공식 카시와라 전기 [2] 와 범프^{Daniel Bump}와 실링^{Anne Schilling}의 결정기저에 관한 책 [4] 의 서문을 읽어봐 주시면 좋을 듯 합니다. 

 

결정 기저를 이해하기 위해서는 양자군에 대해서 먼저 이야기하는 것이 필요합니다. 양자군 ^{quantum group}은 리대수^{Lie algebra} 혹은 좀 더 일반적으로 캣츠-무디 리 대수^{Kac-Moody Lie algebra}의 보편포락대수^{universal enveloping algebra}의 양자화^quantization로 이해할 수 있습니다. 

리 대수의 곱셈은 결합법칙을 만족하지 않기에 곱의 연산의 입장에서는 좋은 대수가 아닙니다. 이에 리대수를 곱의 결합법칙을 만족하는 좋은 대수 속에 집어 넣어서 생각을 하기도 합니다. 이 때 리 대수를 포함하는 대수를 포락대수^{enveloping algebra}라 하고 포락대수 중 가장 큰 대수를 보편포락대수라 합니다.  따라서 양자군은 이름과는 다르게 대수^algebra로 이해해야 하기에 때때로 양자 보편포락대수^{quantized universal enveloping algebra}라고 불리기도 합니다. 

양자군은 수학적으로 풍부하고 깊은 구조를 가지고 있어서 수학의 여러 핵심적인 영역에서 자연스럽게 등장합니다.

 

양자화에 쓰이는 매개변수를 보통 \(q\)로 표시합니다. 좋은 리대수를 \(\mathfrak{g}\)라 표시하면 보통 그것의 보편포락대수를 \(U(\mathfrak{g})\)로 나타내고 대응하는 양자군을 \(U_q(\mathfrak{g})\)로 나타냅니다. 양자군 \(U_q(\mathfrak{g})\)은 보편포락대수 \(U(\mathfrak{g})\)를 비틀어서 양자화하였기 때문에 \(U(\mathfrak{g})\)와 유사한 구조를 가지기도 하지만 다양한 부분에서 다르면서도 훨씬 풍부한 구조를 가집니다. 양자군 \(U_q(\mathfrak{g})\)에서 양자화 매개변수 \(q\)를 1로 보내면 (보통 \(q=1\)이라고 씁니다) 보편포락대수 \(U(\mathfrak{g})\)를 복원할 수 있기에, 양자군의 연구가 자연스럽게 보편포락대수 혹은 리대수의 연구영역을 포함하는 경우가 많습니다. 다만 주의할 부분은 개념적으로는 \(q=1\) 과정이 쉬워 보이지만 수학적으로 의미있게 정의하기 위해서는 깊은 수학적 방법론이 필요합니다. 보편포락대수의 대수적 구조에서는 상쇄되거나 구분할 수 없는 것들이 양자화를 통해서 구분할 수 있게 되어 드러나는 경우가 많이 있습니다. 해결하기 힘든 수학적 문제들을 양자화된 세팅으로 옮겨서 해결하기도 하고, 양자화하기 전에 관찰하기 힘들었던 수학적 사실을 양자화한 후 새롭게 발견하기도 합니다. 결정기저의 발견도 이러한 선 상에 있습니다.

 

양자군 \(U_q(\mathfrak{g})\)에서 \(q=1\) 과정을 취하면 보편포락대수 \(U(\mathfrak{g})\)를 복원하는 것처럼 \(q\)에 다른 값을 취할 수 있습니다. 많은 경우에 \(q=1\) 경우와 유사하지만 \(q=0\) 일 때는 흥미로운 상황이 발생합니다. 위에서 언급했듯이 \(q\)를 특별한 값으로 치환하는 것은 수학적으로 깊고 복잡한 방법이 요구됩니다. 특히 \(q=0\)인 경우는 특이점인 경우로 더 섬세하고 복잡한 방법이 필요합니다. 하지만 \(q=0\) 과정을 거친 후 나온 결과물은 놀랍도록 간결하면서도 양자군의 복잡한 대수적 구조들을 명확하게 담고 있습니다. 이것을 개념적으로 설명하면, 섬세한 방식을 통해서 \(q\)를 0으로 대입하였기에 여러 복잡한 항들이 모두 0으로 바뀌어 없어지고 양자군의 핵심적 구조만 남는다고 이해할 수 있습니다. 양자군 \(U_q(\mathfrak{g})\)의 반쪽인 부분 대수 \(U_q^-(\mathfrak{g})\)에 섬세한 방식으로 \(q=0\) 과정을 적용하여 얻어진 벡터공간의 특별한 기저를 결정기저라고 하고 이를 간단히 \(B(\infty)\)라고 표시합니다. 또한 이러한 \(q=0\) 과정은 양자군의 좋은 모듈에 대해서도 동일하게 적용할 수 있습니다. 특히 특정한 조건을 만족하는 양자군의 최고치 모듈^{highest weight module}도 결정기저를 가지고 있고, 이를 보통 \(B(\lambda)\) 라 표시합니다. 이때 \(\lambda\)는 최고치^{highest weight}를 의미합니다. 

 

결정기저 \(B(\infty)\)와 \(B(\lambda)\)는 양자군의 반쪽 \(U_q^-(\mathfrak{g})\)와 최고치 표현 \(V(\lambda)\)의 핵심적인 성질들을 드러냅니다. 예를 들면 결정기저는 등급 ^graded이 있는 집합으로 볼 수 있는데 등급에 따른 원소의 개수를 세면 표현론에서 중요한 불변량인 특성^character과 일치합니다. 양자군의 대표적인 생성자인 셰발리 생성자^{Chevalley generators} \(e_i\)와 \(f_i\) (단, \(i\)는 인덱스 집합 \(I\)의 원소)로 부터 결정기저 상의 연산자를 자연스럽게 유도할 수 있습니다. 이러한 결정기저 상에서의 연산자를 결정 연산자^{crystal operator}라 부르고 이를 각각 \(\tilde{e}_i\)와 \(\tilde{f}_i\)로 표시합니다. 이 두 결정 연산자는 서로 역원같이 행동하는 성질이 있습니다. 즉 결정기저의 원소 \(b\)와 \(b’\)에 대해서

\(\tilde{f}_i(b) = b’ \qquad \Longleftrightarrow \qquad b = \tilde{e}_i(b’)\)

를 만족합니다. 이러한 결정 연산자는 자연스럽게 결정기저를 조합적인 대상으로 변환시켜 줍니다. 결정기저 (\(B(\infty)\) 혹은 \(B(\lambda)\))를 꼭지점들의 집합이라 생각하고, 꼭지점들 사이의 \(i\)라는 색이 있는 화살표를 아래와 같이 정의해서 그려줍니다.

 

\(b \buildrel i \over \longrightarrow b’  \qquad \Longleftrightarrow \qquad \tilde{f}_i(b) = b’\)

 

그러면 결정 연산자와 같이 결정기저를 생각하면 자연스럽게 색이 있는 유향그래프^{directed graph}로 이해할 수 있습니다. 이 그래프를 결정 그래프^{crystal graph}라 합니다. 이 결정 그래프는 중요한 불변량인 특성^character을 꼭지점들을 통해서 드러내고 셰발리 생성자 \(e_i\)와 \(f_i\)의 작용을 결정 연산자 \(\tilde{e}_i\)와 \(\tilde{f}_i\)를 통해서 화살표로 나타내 줌으로서 양자군과 그것의 모듈의 구조를 조합적으로 해석하고 이해할 수 있게 해줍니다. 따라서 결정 그래프를 통해서 양자군의 표현론은 대수적 조합론과 자연스럽게 연결됩니다. 

 

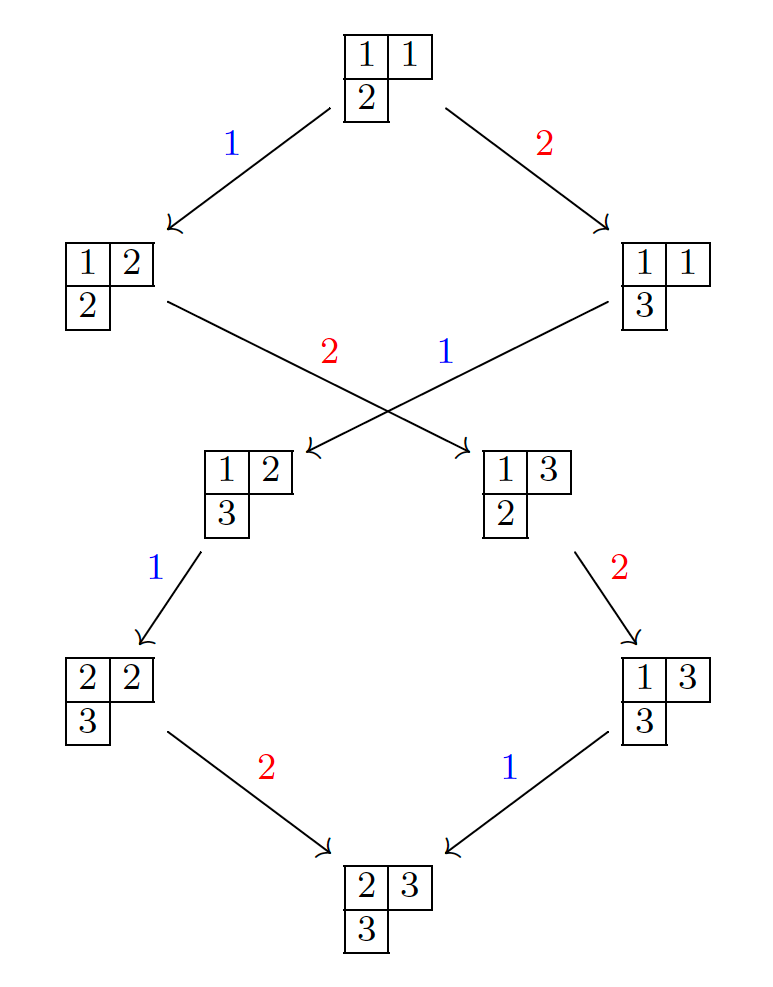
결정 그래프를 통한 표현론과 대수적 조합론 사이의 연결은 단순히 유향그래프로 나타낼 수 있다는 것을 넘어서 중요한 조합적 대상들과 핵심적으로 연결됩니다. 예를 들면 조합론에서 중요한 역할을 맡고있는 대상인 분할^partitions과 타블로^tableaux는 결정기저 이론를 통해 타입 \(A\)의 양자군의 최고치 결정 \(B(\lambda)\)와 연결됩니다. 타입 \(A\)의 최고치 \(\lambda\)는 자연스럽게 특정한 분할로 해석할 수 있고, 결정 \(B(\lambda)\)의 원소들은 분할 \(\lambda\)에 연관된 반표준 영 타블로^{semistandard Young tableaux}들과 대응합니다. 또한 결정 연산자는 반표준 영 타블로의 조합적 특성으로 부터 계산가능합니다. 이러한 조합적 해석은 자연스럽게 대칭다항식^{symmetric polynomial}과 연결되어, 분할과 영 타블로 그리고 대칭다항식의 고전적인 결과들을 결정 이론을 통해서 해석가능하게 해줍니다.  타블로와 대칭다항식에 대한 자세한 내용은 관련 HORIZON의 기사 [5] 를 참조해 주시면 좋을 듯 합니다.  그림1은 타입 \(A_2\)의 최고치 결정 \(B(\Lambda_1 + \Lambda_2)\)를 분할 \((2, 1)\)의 반표준 영 타블로를 이용해서 그린 결정 그래프입니다.  결정기저 이론은 단순한 추상적 구조를 넘어서 조합적 계산과 응용이 가능하게 정립했다는 점에서 큰 의미를 가지며, 표현론과 조합론 두 영역 모두에서 상호보완적인 발전을 이끌어내는 역할을 했다고 평가할 수 있습니다. 

 

 

 

 

 

필자는 카시와라 교수님과 양자군의 범주화와 클러스터 대수에 대해서 함께 연구를 하고 있습니다. 첫 공동논문이 2013년에 출판되었으니 10년이 훌쩍 넘는 기간동안 함께 연구를 진행하였네요. 고등과학원은 저와 카시와라 교수님 모두에게 특별한 인연이 있는 곳입니다. 저는 박사학위를 받은 후 고등과학원에서 연구원 생활을 하였고, 카시와라 교수님은 2016년부터 약 10년간 고등과학원의 KIAS Scholar 였습니다. 카시와라 교수님이 KIAS Scholar로 방문하시면 제가 방문기간 동안 찾아뵈어 같이 수학에 대해서 이야기를 나누었습니다.  고등과학원 후문 근처의 자주 갔던 작은 카페에서 커피를 마시며 수학에 대해서 이야기하고, 연구실로 걸어가면서 많은 아이디어를 나누었던 것이 생각납니다. 놀라운 수학적 통찰력을 가진 큰 수학자의 모습과 동시에 소탈하고 인간적인 모습을 보면서, 저는 학문적으로도 인간적으로도 많은 것을 깨닫고 배웠던 것 같습니다. 이 지면을 빌어 깊은 감사를 드리며 그 동안 쌓아온 놀라운 업적과 수학에 대한 변함없는 열정에 존경을 표합니다.