[2월의 퍼즐] 소수가 품은 소수

소수는 언제나 수학자들을 매혹하는 존재이다. 소수가 가진 아름다운 성질, 놀라운 성질, 기묘한 성질들은 수학 뿐 아니라 여러 과학 분야에도 뜻밖의 모습으 로 등장하곤 한다.

수학자들이 소수에서 발견한 신기한 사실 가운데 하나로 “소수가 품은 소수” 가 있다. 소수가 주어졌을 때, 몇 개의 숫자를 지우고 남은 숫자로 이루어진 수가 다시 소수가 되는 경우를 생각해 보자.

예를 들어, 지난 해의 연도인 2017은 소수이고, 여기서 2와 0을 지우면 소수 17이 된다. 더 간단히 0, 1, 7을 지워 2를 만들 수도 있고, 2, 0, 1을 지워 7을 만들 수도 있다. 이 경우, 2, 7, 17을 2017이 품은 소수라 하자. 물론 2017 자신도 2017이 품은 소수이다. 그렇지만 숫자의 순서를 바꾼 71은 2017이 품은 소수가 아니다.

예를 하나 더 들어 보면, 모든 자리의 숫자가 소수가 아닌 104869는 소수이고,
이 소수가 품은 소수로는 

19, 89, 109, 149, 1049, 1489, 10489, 104869

가 있다.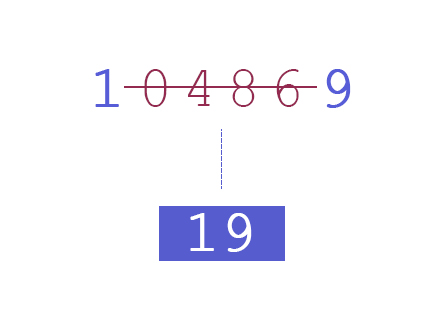이제 이런 질문을 생각해 보자. 소수의 유한 집합 중에 다음 성질을 만족하는 것이 있을까?

모든 소수는 이 집합의 어떤 원소를 품고 있다.

증명이 좀 복잡하기는 해도, 다음 26개의 소수가 이런 성질을 만족함이 알려져 있다. 즉, 어떠한 소수를 생각하더라도 거기서 숫자를 적당히 지우면 다음 26개의 소수 중 하나를 얻을 수 있다.

2, 3, 5, 7, 11, 19, 41, 61, 89, 409, 449, 499, 881, 991,
6469, 6949, 9001, 9049, 9649, 9949, 60649, 666649, 946669,
60000049, 66000049, 66600049

상황을 뒤집어, 합성수가 품은 합성수를 생각하면 어떨까? 이 경우, 어떠한 합성수를 생각하더라도 거기서 숫자를 적당히 지우면 다음 32개의 합성수 중 적어도 하나를 반드시 얻을 수 있다는 것이 알려져 있다.

4, 6, 8, 9, 10, 12, 15, 20, 21, 22, 25, 27, 30, 32, 33, 35, 50,
51, 52, 55, 57, 70, 72, 75, 77, 111, 117, 171, 371, 711, 713, 731

이번 호의 퍼즐은 2의 거듭제곱이 품은 2의 거듭제곱을 찾는 것으로 하자. 즉, 2의 거듭제곱 1, 2, 4, 8, 16, …의 부분 집합이면서 다음 성질을 만족하는 유한 집합 중 가장 작은 것은 무엇일까?

2의 거듭제곱 1, 2, 4, 8, 16, … 각각은 이 집합의 어떤 원소를 품고 있다.