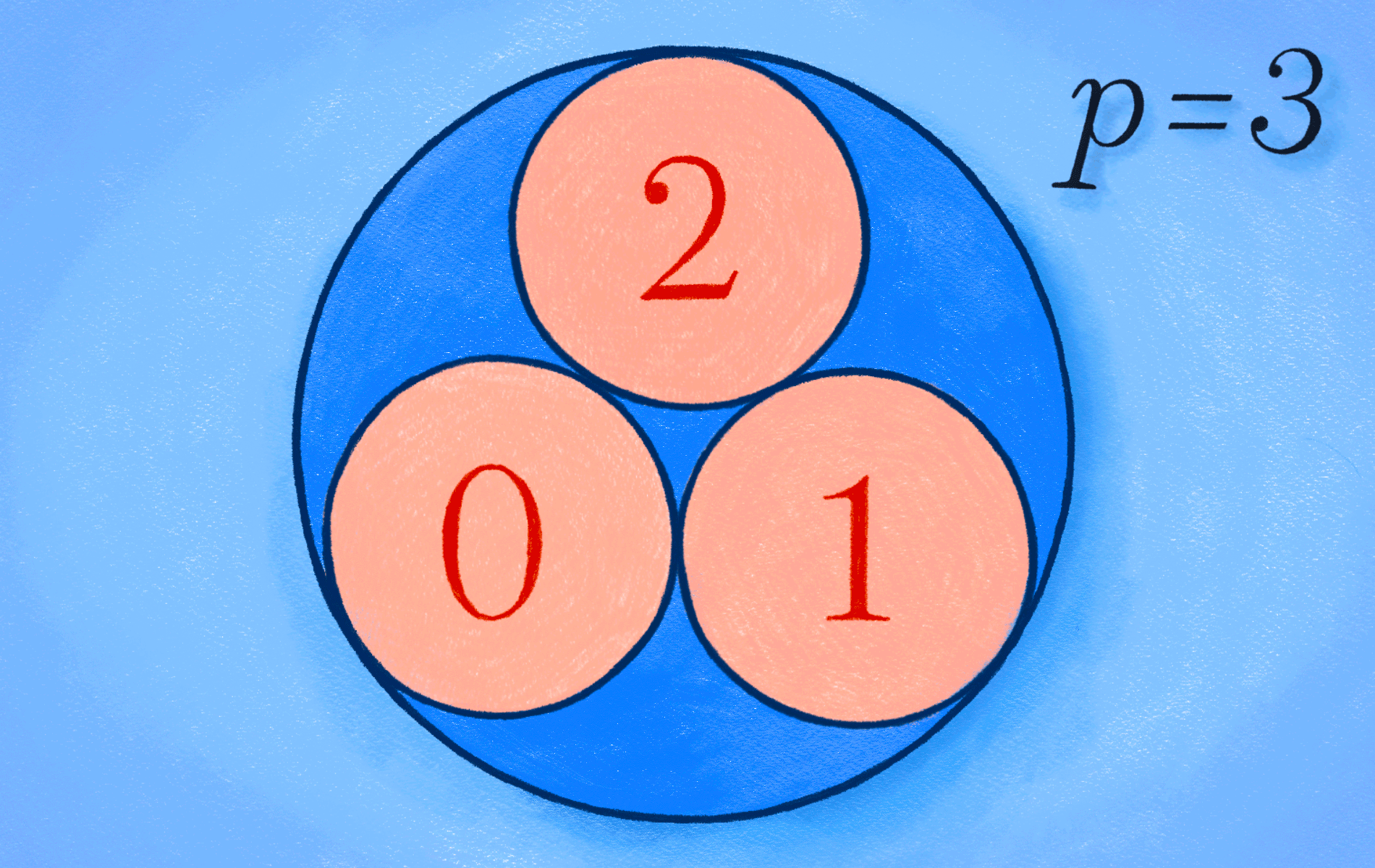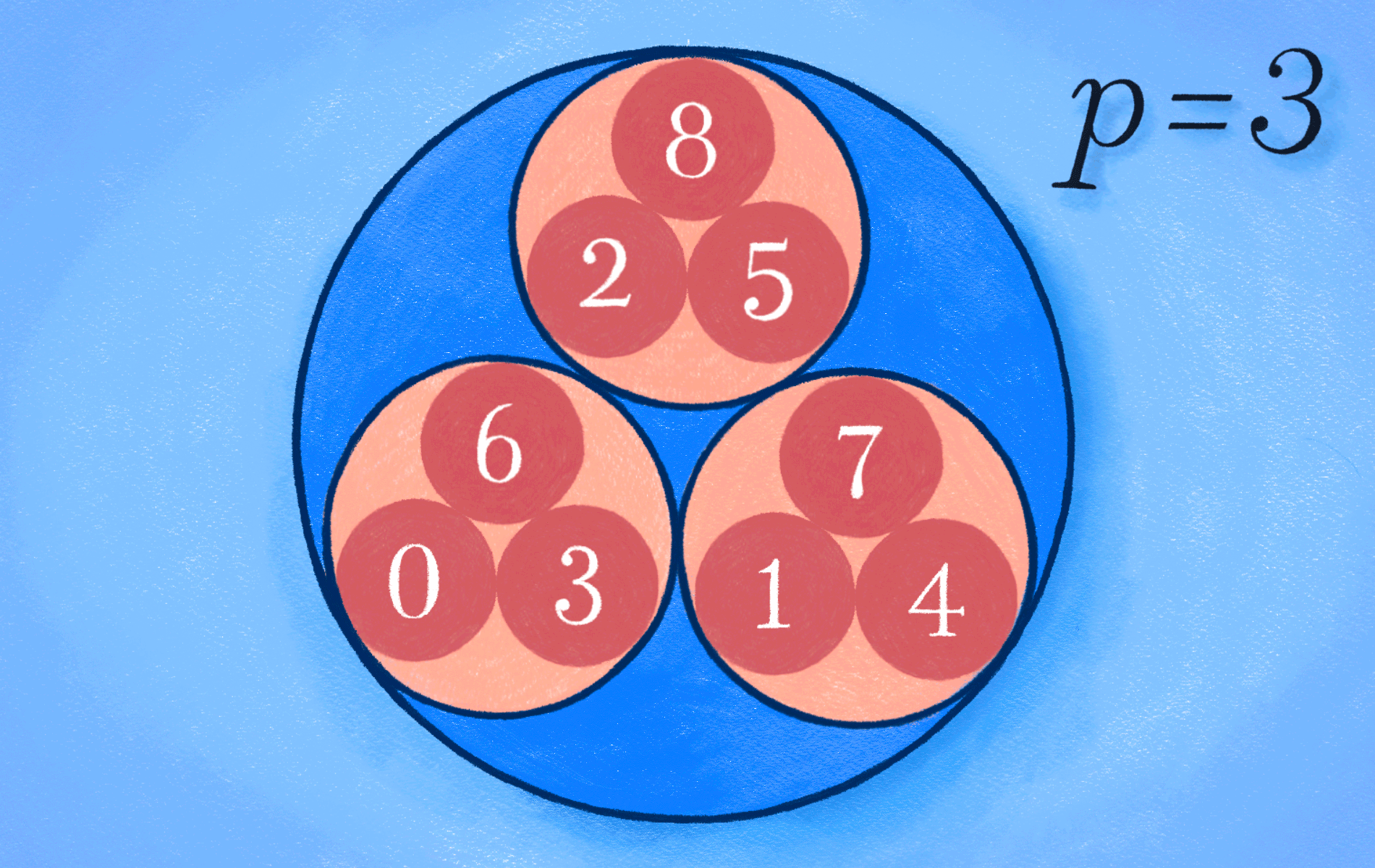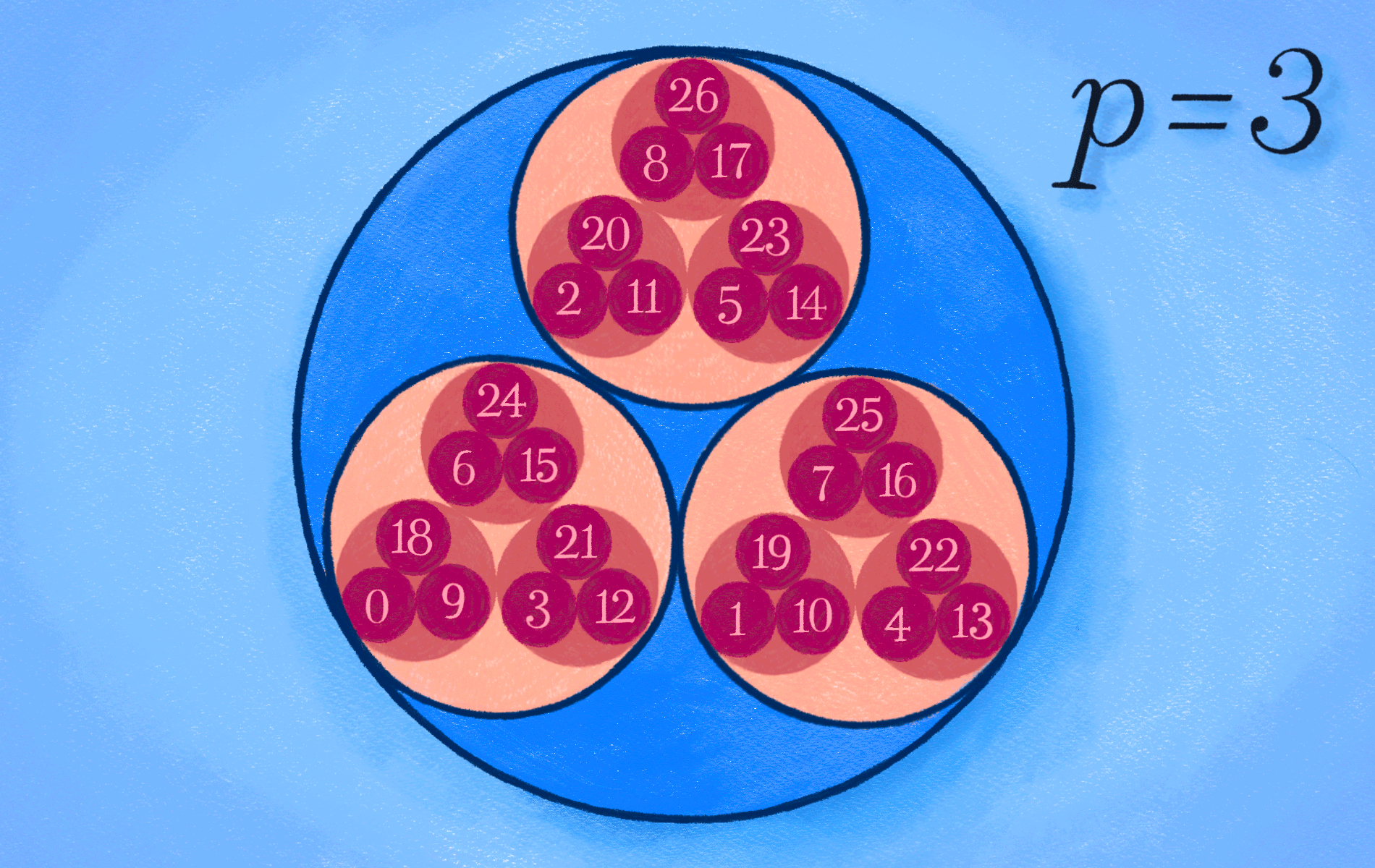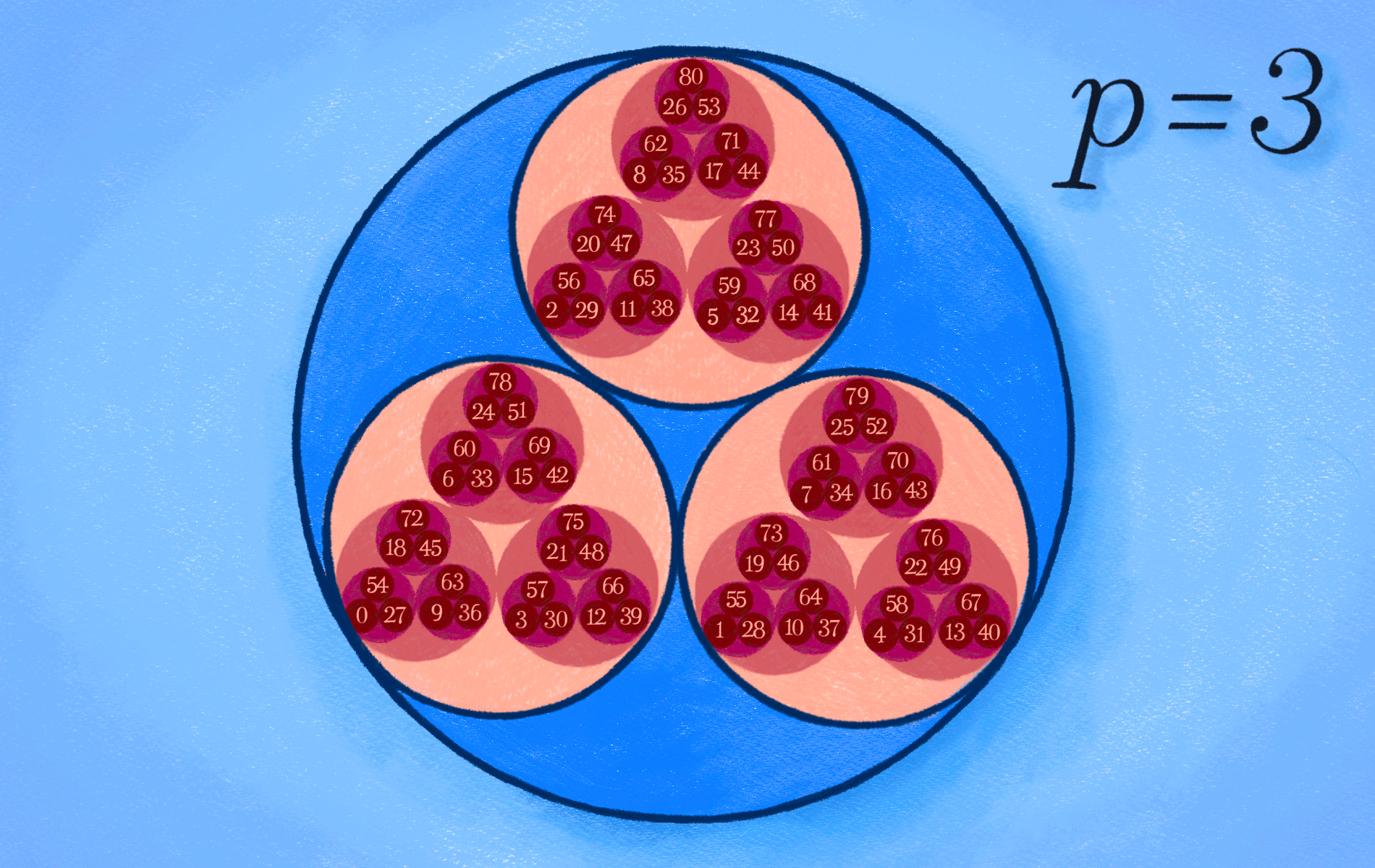p진 해석과 기하 [2]: p진수에 대한 소개

P-ADIC ANALYSIS AND GEOMETRY
Introduction to p-adic numbers

이번 연재에서는 ‘\(p\)진수’라는 수 체계에 기반한 해석과 기하를 소개하고자 한다. 실수나 복소수처럼 \(p\)진수 위에서도 ‘자연스러운’ 해석과 기하 이론을 전개할 수 있고, 그 결과가 정수론에 유용하게 쓰이는 반면, 실수와 복소수와는 다른 생소한 현상도 많이 나타난다. 이번 연재를 통해 \(p\)진수의 해석과 기하의 여러 측면을 소개하고, 정수론에서 \(p\)진수의 유용성을 보여주고자 한다. 지난 글 “p진 해석과 기하 [1]: 수의 크기를 재는 여러 방법?”에 이어, 이번 글에서는 \(p\)진수와 \(p\)진 거리에 대해 소개하려 한다.

***

지난 글 요약

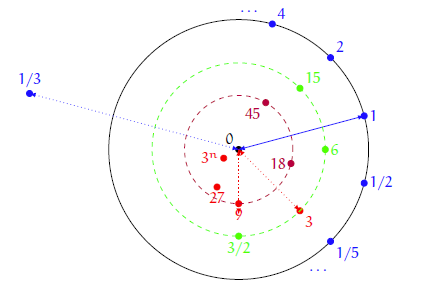
서론에 해당하는 지난 글 “p진 해석과 기하 [1]: 수의 크기를 재는 여러 방법?”에서 “모두가 센터일 수는 없는 것일까?”라는 뜬금없는 질문을 던진 뒤, 이번 연재에서 소개할 \(p\)진수^{\(p\)-adic numbers}라는 수 체계에서는 원판 위의 모든 점이 중심이 된다고 주장하였다. (다만 이렇게 주장만 하고 정작 \(p\)진수가 무엇인지는 설명하지 않았다. 이번 글에서야 본격적으로 \(p\)진수가 등장한다.)

정의야 어떻든 간에, \(p\)진수라는 수 체계를 소화하기 위해서는 수를 물리적 직관에서 해방시키는 사고과정이 선행되어야 한다. 이를 위해 “‘수’란 무엇인가”라는 수학 입장에서의 최상위 거대담론에 해당하는 질문은 던지고, 여기에 실수^{real numbers}라는 ‘하나의 답’으로 향하는 여정을 보여주었다. 그리고 ‘실수’를 얻어내는 과정에서 물리적 직관에 종속된 공리를 추출하고 분리해 내는 작업을 통해 \(p\)진수라는 수 체계를 얻어낼 수 있다고 결론지었다.¹ 굳이 비유하자면, 유클리드 기하에서 물리적 직관으로는 너무 당연해 보이는 유클리드 공리를 추출하고 분리해 내면서 기존에 보이지 않던 새롭고 흥미로운 기하를 얻어내는 것과 유사한 사고과정이 아닐까 한다.

‘절대값’ 공리: 지난 편 요약. 직관적으로 말하면 ‘실수’란 ‘유리수를 무한히 근사하는 수’이다. 여기에서 우리는 은연중에 물리적 직관에 따라 유리수의 크기를 재는 법, 즉 절대값을 고정하였다. 가령\(1,000,000\)은 당연히 매우 큰 수이고, 따라서 그 역수인 \(0.000001\)은 매우 작은 수여야 할 것이다. 하지만

“왜 \(1,000,000\)의 절대값이 \(1\)보다 커야만 하는가?”

이 질문에 대한 답을 구하기 위해 지난 편에 소개한 절대값의 정의를 되새겨 보자.

정의. 각 유리수에 실수를 대응시키는 함수 \(|\bullet|\colon \alpha\mapsto |\alpha|\)가 아래 (Abs1)부터 (Abs4)까지의 네 가지 성질을 만족하는 경우, 이 함수 \(|\bullet|\)를 유리수의 절대값^{absolute value}이라고 부른다.

(Abs1) 모든 \(\alpha\)에 대해서 \(|\alpha|\geqslant0\)을 만족한다.
(Abs2) \(|\alpha| = 0\)을 만족하는 유일한 유리수는 \(\alpha=0\)이다.
(Abs3) 임의의 \(\alpha,\beta\)에 대해서 \(|\alpha\cdot\beta|= |\alpha| \cdot |\beta|\)를 만족한다.
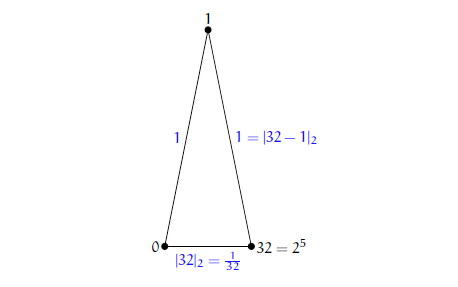
(Abs4) (삼각 부등식) 임의의 \(\alpha,\beta\)에 대해서 \(|\alpha + \beta| \leqslant |\alpha| + |\beta|\)를 만족한다. ([그림1] 참조)

우리가 ‘자연스럽게 사용하고 있는 절대값’의 경우 아래 아르키메데스 성질을 추가로 만족한다.

(Abs5) (아르키메데스 성질) 양의 정수 \(n\)이 커짐에 따라 \(|n|\)이 양의 무한대로 발산한다.

이제 다시 질문으로 돌아와서 절대값의 정의에 포함된 (Abs1-4)의 경우에는 \(1,000,000\)의 절대값이 \(1\)보다 작거나 같아도 전혀 모순이 생기지 않는다. (일례로 나중에 소개할 \(2\)진 절대값과 \(5\)진 절대값에 대해서는 \(1,000,000\)의 절대값이 \(1\)보다 작으며, \(2\)와 \(5\)를 제외한 소수 \(p\)에 대한 \(p\)진 절대값에 대해서는 \(1,000,000\)과 \(1\)의 절대값이 같다.) 따라서 아르키메데스 성질이 \(1,000,000\)의 절대값이 \(1\)보다 크도록 강제한다고 결론지을 수 있다.² 

비아르키메데스 절대값

아르키메데스 성질은 수에 대한 물리적 직관에 따르면 너무나도 자연스러워 보인다. 하지만 많은 근원적인 성질들은 절대값의 공리인 (Abs1-4)만 사용해서 얻어낼 수 있고, 또 아르키메데스 성질은 나머지 네 공리와 독립적이다. 더 나아가서는 아르키메데스 공리를 만족하지 않는 유리수의 절대값, 즉 비^非아르키메데스 절대값^{non-archimedean absolute value}을 거리의 개념으로 사용하여 수를 물리적 직관에서 해방시킬 수 있다.

그렇다면 유리수에서 정의되는 비아르키메데스 절대값은 정말 존재하는 것일까? 존재한다면 어떤 절대값이 있을까?

자명한 절대값^{trivial absolute value}. 자명한 절대값 \(|\bullet|_{\rm triv}\)은 아래와 같이 정의된다.

\begin{equation}
|\alpha|_{\rm triv} = \left\{
\begin{array}{ll}
1 & \text{if }\alpha\ne0\\
0 & \text{if }\alpha=0.
\end{array}
\right.\quad \cdots \quad (1)
\end{equation}

‘자명한 절대값’은 이름만큼 자명하게 절대값의 공리 (Abs1-4)를 모두 만족한다. 하지만 자명한 절대값에 대해 유리수 \(\alpha\) 근처에 있는 수는 \(\alpha\)밖에 없다. (사실 \(|\alpha-\beta|_{\rm triv}<1\)을 만족하려면 \(\alpha=\beta\)여야 한다.) 즉 자명한 절대값은 너무 자명해서 재미도 없고 쓸모도 없는 절대값이다.

\(p\)진 절대값^{\(p\)-adic absolute value}. 먼저 소수 \(p\)를 하나 고른다. 예를 들어 \(p\)를 \(2,3,5,7,\cdots\) 중에 임의로 하나 고르자. 그리고 \(p\)진 절대값 \(|\bullet|_p\)는 아래와 같이 정의하자.

먼저 절대값의 정의에 의해 \(|0|_p=0\)이어야 한다. 만약 \(\alpha\)가 \(0\)이 아닌 유리수라면, \(p\)에 나누어지지 않는 서로 소인 정수 \(a,b\)와 정수 \(r\)이 있어서
\[\alpha=p^r\cdot (a/b)\]로 유일하게 표현할 수 있다. 그러면 \(\alpha\)의 \(p\)진 절대값은
\begin{equation}
|\alpha|_p = |p^r \cdot (a/b)|_p := p^{-r}
\quad \cdots \quad (2)
\end{equation}으로 정의한다. 어떤 소수 \(p\)에 대해서도 \(|\bullet|_p\)는 절대값의 공리 (Abs1-4)를 모두 만족하며, 아르키메데스 공리는 만족하지 않음을 보일 수 있다.

예를 들어 \(p=3\)로 두면 \(3\)진 절대값은
\begin{align*}
|1|_3 & = 1\\
|2|_3 & = 1\\
|3|_3 & = 1/3 \\
|4|_3 & = 1\\
|5|_3 & = 1\\
|6|_3 & = 1/3\\
&\vdots \\
|9|_3 & = 1/9,\ |27|_3 = 1/27,\ |81|_3 = 1/81 ,\ \cdots
\end{align*}임을 확인할 수 있다.

여기에서 다음과 같은 사실을 어렵지 않게 관찰할 수 있다.

1. 모든 정수 \(n\)에 대해 \(|n|_3 \leqslant 1\)이기에, \(3\)진 절대값은 아르키메데스 성질 (Abs5)을 만족하지 않는다.
2. \(3\)을 곱할수록 \(3\)진 절대값은 점점 더 작아지고, \(3\)으로 나눌수록 \(3\)진 절대값은 점점 더 커진다. 바꾸어 말하면 정수 \(n\)의 \(3\)진 절대값은 \(3\)이 \(n\)을 몇 번 나누는지에 의해 결정되며, \(3\)이 \(n\)을 많이 나눌수록 \(n\)의 \(3\)진 절대값 \(|n|_3\)은 작아진다.

마찬가지로 임의의 소수 \(p\)에 대해 \(p\)진 절대값도 모든 정수 \(n\)에 대해 \(|n|_p \leqslant 1\)을 만족하며, \(p\)를 곱할수록 \(p\)진 절대값은 점점 더 작아지고 \(p\)로 나눌수록 \(p\)진 절대값은 점점 더 커진다.

\(p\)진 절대값과 합동^congruence. 처음 보기에는 \(p\)진 절대값이 상당히 이상해 보일 수도 있다. 소수 \(p\)를 \(3\)일 때 일반적인 상식으로 보면 큰 수인 \(3^{10} = 59049\)는 \(3\)진 절대값에 대해서 ‘매우 작은’ 수인 반면에, 거기에 \(1\)을 뺀 수인 \(59048\)의 \(3\)진 절대값은 \(1\)이 되어버린다. (\(59048\)은 \(3\)에 나누어 떨어지지 않기 때문이다.) 하지만 정수론의 관점에서는 \(p\)진 절대값이 자연스럽게 등장하는데, 사실 \(p\)진 절대값이란 \(p\)의 모든 거듭제곱에 대한 합동^congruence을 절대값이라는 개념을 빌려서 우아하게 포장한 것에 다름 아니기 때문이다.

잠시 구체적인 예를 들어, \(p=3\)으로 두고 두 정수 \(1\)과 \(354295\) 사이의 \(3\)진 거리를 생각하면
\[ |354295-1|_3 = |2\cdot 3^{11}|_3 = 3^{-11}\]
이 되어, \(1\)은 \(354295\)을 \(3^{-11}\)이라는 매우 작은 오차로 근사함을 알 수 있다. 위 식을 조금 다르게 쓰면 \(354295\)을 \(3^{11}\)로 나눈 나머지가 \(1\)이 되기 때문에 아래와 같은 합동식을 얻는다.
\[
354295 \equiv 1 \bmod{3^{11}}.
\]

이 관찰을 일반적으로 서술하면 다음 보조정리를 얻는다.

보조정리. 두 정수 \(a,b\)가 주어졌을 때
\begin{equation}\label{eq:cong}
|a-b|_p\leqslant p^{-n}\quad \Longleftrightarrow \quad a\equiv b \bmod{p^n}.
\quad \cdots \quad (3)
\end{equation}

즉 \(a\)와 \(b\)가 \(p\)의 더 큰 거듭제곱에 대해 합동일수록 둘 사이의 \(p\)진 거리는 가까워진다.

따라서 \(p\)진 절대값을 정수 혹은 유리수에 국한하면 단순히 \(p\)의 모든 거듭제곱에 대한 합동을 생각하는 것과 차이가 없다. 하지만 아르키메데스 절대값 대신에 \(p\)진 절대값을 사용하여 실수의 건설 방법을 따라하게 되면 소위 \(p\)진수라는 수 체계를 얻게 되고, \(p\)진수에서도 실수에서처럼 해석학과 기하학이 가능하다.³ 정수론의 합동 연산에서 출발해서 해석과 기하에 다다르는 연결고리가 바로 \(p\)진 절대값이다.

유리수의 절대값 분류. 그러면 유리수는 어떤 절대값을 가질 수 있을까? 우리가 놓친 새로운 미지의 절대값이 있지는 않을까? 아래 정리가 그 해답을 제시한다.

정리 (오스트롭스키의 정리^{Ostrowski’s theorem}). 임의의 유리수의 절대값 \(|\bullet|:\alpha\mapsto|\alpha|\)은 다음 세 가지 중 하나에 해당한다. 

1. 어떤 실수 \(0<s\leqslant 1\)가 있어서 모든 유리수 \(\alpha\)에 대해 \(|\alpha| = |\alpha|_\infty^s\)를 만족한다.
2. 어떤 소수 \(p\)와 양의 실수 \(s\)가 있어서, 모든 유리수 \(\alpha\)에 대해 \(|\alpha| = |\alpha|_p^s\)를 만족한다.
3. 모든 유리수 \(\alpha\)에 대해 \(|\alpha| = |\alpha|_{\rm triv}\)를 만족한다.

첫 번째 경우는 아르키메데스 절대값이고, 나머지 경우는 비아르키메데스 절대값이다.

\(p\)진 전개와 \(p\)진수

오스트롭스키 정리에 의하면 유리수의 절대값은 실질적으로는 1. ‘자연스러운 절대값’ \(|\bullet|_\infty\) (혹은 아르키메데스 절대값), 2. 임의의 소수 \(p\)에 대해 \(p\)진 절대값 \(|\bullet|_p\), 그리고 3. 자명한 절대값 \(|\bullet|_{\rm triv}\)이 있을 수 있다. 다만 앞에서 언급한 대로 자명한 절대값은 무시하여도 상관없다.

유리수의 절대값 \(|\bullet|\)이 위의 세 가지 중 하나로 주어지면, 임의의 두 유리수 \(\alpha,\beta\) 사이의 거리를 \(|\alpha-\beta|\)라고 생각할 수 있다. 실수를 만드는 법은, 자연스러 절대값 \(|\bullet|_\infty\)이 정의한 거리에 대해서 ‘유리수와 무한히 가까운 수’를 엄밀하게 정의하여, 이렇게 정의된 수를 사용해 ‘유리수 사이의 빈 공간’을 채운 것으로 이해할 수 있다.

그렇다면 임의의 소수 \(p\)를 고정했을 때 다음과 같은 질문을 할 수 있다.

“\(p\)진 절대값 \(|\bullet|_p\)이 만드는 거리에 대해서
‘유리수와 무한히 가까운 수’를 어떻게 정의할 것인가?”

이 질문에 대한 답이 바로 \(p\)진수이다. 이번 글에서는 \(p\)진수를 수학적으로 엄밀하게 접근하기보다는, 실수와의 단순한 비유를 통해 대략적으로 묘사하고자 한다.

먼저 실수인 원주율 \(\pi\)를 다시 살펴보자. 원주율 \(\pi\)를 십진법으로 전개하여 정수 부분을 \(a_0:=3\)으로, 소숫점 아래 \(n\)번째 숫자를 \(a_n\)으로 놓자. 예를 들면,
\begin{align*}
\pi &= 3.1415926535 8979323846 2643383279\dots \\
a_{0}& = 3, \quad a_{1}=1, \quad a_2 = 4,\quad a_3=1,\quad \cdots
\end{align*}그러면 \(\pi\)를 아래와 같은 수렴하는 무한급수로 볼 수 있다.
\begin{align*}
\pi &= a_0 + a_1\cdot 10^{-1} +\cdots + a_n\cdot 10^{-n} + O(10^{-n})\\
&\vdots\\
\pi & = \sum_{n=0}^{\infty} a_n \cdot 10^{-n} = a_0 + a_1\cdot 10^{-1} +\cdots + a_n\cdot 10^{-n} +\cdots.
\end{align*}비슷하게 임의의 실수 \(\beta\)의 십진법 전개 역시 위와 유사한 무한급수로 생각할 수 있다.

실수의 건설과 비슷한 전략을 아르키메데스 절대값 대신 \(p\)진 절대값이 정의하는 거리를 사용하면 \(p\)진수를 만들어낼 수 있다.

정의 (\(p\)진수). 소수 \(p\)를 고정하면, \(p\)진수는
\begin{equation}\label{eq:alpha}
\alpha = \sum_{n=-N}^{\infty} a_n p^{n} \qquad \left (\text{모든 }n\text{에 대해서 }a_n\in\{0,1,\cdots,p-1\} \right )
\quad \cdots \quad (4)
\end{equation}로 표현되는 ‘수’이다. 덧셈, 뺄셈, 곱셈 등의 연산은 십진법으로 표현된 실수의 연산과 비슷하게 정의할 수 있으며, \(0\)이 아닌 \(p\)진수⁴는 곱셈의 역원(즉 나눗셈)이 정의된다.

마지막으로 \(\alpha\)가 \(0\)이 아닌 경우
\[
|\alpha|_p:= p^{-n_0}
\]로 정의하는데, 여기에 \(n_0\)는 \(a_n\)이 \(0\)이 아닌 가작 작은 \(n\)으로 둔다.

이제 실수와 \(p\)진수를 잠시 비교해 보자. 만약 \(\alpha = \sum_{n=-N}^{\infty} a_n p^{n}\)로 씌여지는 \(p\)진수를 생각하면, 각 \(a_n\)은 실수의 경우 소숫점 아래 \(n\)번째 숫자처럼 생각할 수 있다. 실수를 ‘십진법 전개가 소숫점 아래로 무한히 어어지는 수’라고 생각하면, 위의 \(p\)진수의 정의와의 유사점을 찾을 수 있다.

여기에서 한 가지 주의할 점은 \(p\)진수의 무한급수 표현 (4)는 보통 실수에서 무한대로 발산해 버린다. 따라서 \(p\)진수의 무한급수 (4)를 다룰 때에는 실수에서의 수렴성은 잊어버리고 \(p\)진 절대값이 정의하는 수렴성을 생각해야 한다. 사실 \(p\)의 거듭제곱의 \(p\)진 절대값은 ‘매우 빠르게’ 작아지면서 \(0\)에 접근하며, 따라서 위의 무한급수 (4)는 \(p\)진 절대값에 대해서 수렴하는 극한값이 된다.⁵

다음 주제로 넘어가기 전에 유리수를 어떻게 \(p\)진수로 볼 수 있는지 설명하고자 한다. 먼저 정수 \(\alpha\)의 경우 \(\alpha = \sum_{n=0}^N a_np^n\)인 형태의 \(p\)진 전개를 어렵지 않게 얻을 수 있다. 예를 들어 \(p=5\)라고 하면 \(\alpha = 136\)은

\[
136 = 1 + 2\cdot 5^1 + 0\cdot 5^2 + 1\cdot 5^3
\]임을 얻는다.

일반적인 유리수에 대해서는 일반론으로 다루는 대신 다음의 예시로 대신하자. 소수 \(p=5\)로 고르고, \(\alpha=\frac{3}{250}\)이라고 하자. 먼저 \(\alpha = 5^{-3}\cdot \frac{3}{2}\)이기에 \(\frac{3}{2}\)를 \(5\)진수로 표현하면 \(\alpha\)의 \(5\)진수 표현을 얻을 수 있다. 그러면 \(\frac{3}{2}\)를 \(5\)진수로 표현을 얻기 위해 다음 합동 선형방정식을 생각해 보자.
\begin{align*}
\beta_0 &= 4 &\text{는 }2\beta_0\equiv3\bmod{5}\text{를 만족한다.}\\
\beta_1 &= 4+2\cdot 5 &\text{는 }2\beta_1\equiv3\bmod{5^2}\text{를 만족한다.}\\
\beta_2 &= 4+2\cdot 5 + 2\cdot 5^2 &\text{는 }2\beta_2\equiv3\bmod{5^3}\text{를 만족한다.}\\
\beta_3 &= 4+2\cdot 5 + 2\cdot 5^2 +2\cdot 5^3 &\text{는 }2\beta_3\equiv3\bmod{5^4}\text{를 만족한다.}\\
&\vdots&
\end{align*}
따라서 \(5\)진 절대값에 대해 수열 \(\beta_n\)의 극한은 아래와 같은 \(5\)진수가 될 것이다.
\begin{equation}\label{eq:r}
\beta:= 4 + \sum_{n=1}^\infty 2\cdot 5^n;
\quad \cdots \quad (5)\end{equation}이렇게 정의된 수열 \(\beta_n\)은 \(5\)진 절대값에 대해 \(\beta\)로 수렴한다. (즉 \(|\beta-\beta_n|_5 = 5^{-n}\)을 만족한다.) 또한 앞에서 언급한 정수의 합동식과 \(5\)진 절대값과의 관계 (3)을 사용하면
\[
|2\beta_n – 3|_5 \leqslant 5^{-n}
\]을 만족하기에 \(|2\beta-3|_5 = 0\), 즉 \(2\beta-3 = 0\)을 얻는다. 따라서 식 (5)에 정의된 \(5\)진수 \(\beta\)가 유리수 \(\frac{3}{2}\)과 같음을 얻는다. 그러므로 \(\alpha = 5^{-3}\cdot\frac{3}{2}\)를 \(5\)진수로 표현하면
\[
5^{-3}\cdot\frac{3}{2} = 5^{-3}\cdot \beta = 4\cdot 5^{-3}+\sum_{n=-2}^\infty 2\cdot 5^n
\]임을 얻는다. 비슷한 방법으로 임의의 유리수 \(\alpha\)를 \(p\)진수로 표현할 수 있다.

초거리 부등식^{ultrametric inequality}: 원판의 모든 점이 중심

실수에서 수열 및 무한급수의 수렴성은 단순하지 않은 문제이다. 예를 들어
\[
\sum_{n=1}^{\infty}\frac{1}{n}
\]은 각 항이 \(0\)으로 수렴함에도 불구하고 급수는 무한대로 발산한다. 일반적으로 어떤 수열이나 급수가 수렴하는지에 대해 다양하고 복잡한 판별법이 존재한다. 하지만 \(p\)진 절대값, 혹은 더 일반적으로 비아르키메데스 절대값에 대해서는 수렴성의 판별이 훨씬 간단하다. 이 때 아래 보조정리가 중요한 역할을 한다.

보조정리. 소수 \(p\)를 하나 고정하자. 그러면 임의의 \(p\)진수 \(\alpha\)와 \(\beta\)에 대해
\begin{equation}\label{eq:ultrametric}
|\alpha+\beta|_p \leqslant \max\{|\alpha|_p,|\beta|_p\}
\quad \cdots \quad (6)
\end{equation}를 만족하며, 만약 \(|\alpha|_p\ne|\beta|_p\)이면 위 부등호 대신 등호가 성립한다.

부등식 (6)은 초거리 부등식^{ultrametric inequality}이라고 부른다. 초거리 부등식에서 삼각부등식 (Abs4)이 유도되므로, 초거리 부등식은 엄격한 삼각 부등식^{strict triangle inequality}으로도 불린다. 그리고 초거리 부등식을 만족하는 절대값은 정확히 비아르키메데스 절대값임도 어렵지 않게 증명할 수 있다.

초거리 부등식은 다음과 같은 따름정리를 가진다.

따름정리. 소수 \(p\)를 고정하고, 유리수의 수열 \(\alpha_n\)을 생각하자. 만약 \(\alpha_n\)이 \(p\)진 절대값에 대해 \(0\)으로 수렴하면 무한급수 \(\sum_{n=0}^{\infty}a_n\) 역시 어떤 \(p\)진수로 수렴한다.⁶

따라서 \(p\)진 절대값에 대한 수열이나 무한급수의 수렴성은 실수에서보다 훨씬 간단하다. 그러므로 \(p\)진 절대값의 생소함을 극복하기만 하면, \(p\)진수의 건설 및 주요 성질을 보이는 것은 실수를 건설하는 것만큼 까다롭지 않다.

이제 초거리 부등식을 ‘기하적’으로 해석해 보자. 두개의 \(p\)진수 \(\alpha\)와 \(\beta\)가 주어졌을 때 초거리 부등식에 의해, 

\[
|\alpha|_p,\quad |\beta|_p,\quad |\alpha+\beta|_p
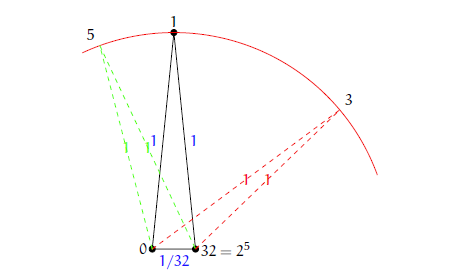
\]중에서 적어도 두 개의 값이 일치해야 하며, 일치하지 않는 값은 나머지 두 개의 값보다 작아야 한다. (만약 \(|\alpha|_p>|\beta|_p\)이면 초거리 부등식은 등식이 되어 \(|\alpha+\beta|_p =|\alpha|_p>\beta|_p\)임을 얻는다.) 따라서 \(p\)진수를 평면의 점으로 표현하면 \(0\), \(\alpha\), \(\alpha+\beta\)인 세 점 만드는 삼각형은 항상 뾰족한 이등변 삼각형이 된다. ([그림3] 참조)

약간 다른 측면으로 초거리 부등식을 보자. 간단한 예시를 위해 \(|\alpha-0|_p\leqslant1\)을 만족하는 \(p\)진수 \(\alpha\)들을 생각해 보자. 만약 \(p\)진수를 평면 위의 점으로 생각한다면, 이 \(\alpha\)들은 원점 \(0\)을 중심으로 반지름 \(1\)인 원판을 이룬다고 생각할 수 있다. 그리고 이 원판에서 임의의 점 \(\beta_0\)를 골라서 \(\beta_0\)를 중심으로 하는 반지름 \(1\)인 원판을 생각하자. (즉 \(|\beta_0|_p\leqslant1\)을 만족하는 \(p\)진수 \(\beta_0\)를 하나 골라서, \(|\beta-\beta_0|\leqslant 1\)인 \(p\)진수 \(\beta\)가 이루는 원판을 생각하자.) 그러면 초거리 부등식에 의해 이 두 원판이 일치하게 된다. 즉 \(p\)진수 \(\alpha\)에 대해
\[
|\alpha-0|_p\leqslant 1 \qquad \Longleftrightarrow \qquad |\alpha – \beta_0|\leqslant 1
\]임을 얻는다. 다시 말하면 원판에서 중심을 바꾸어 가며 같은 반지름의 원판을 그리더라도, 정확히 같은 원판을 얻게 된다. ([그림4] 참조) 이 성질은 추후 연재에 언급하겠지만 \(p\)진 미분방정식 이론에서 흥미로운 ‘부작용’을 낳게 된다.

맺음말

앞에서 본 것처럼 \(p\)진 절대값이 주는 거리의 개념은 우리의 평상시 물리적인 직관에 위배하는 행동을 보이기도 한다. 그렇다면

“왜 \(p\)진수를 공부하는 것인가?”

앞서 보았듯이 \(p\)진 절대값이 정수의 \(p\)의 거듭제곱에 대한 합동을 다른 수학적 언어로 포장한 것이다. (식 (3) 참조) 만약 기초정수론을 조금이라도 접해본 독자라면, 방정식의 정수해를 구하는 문제에서 합동이 얼마나 강력한 도구인지 체감하였을 것이다. 그리고 약간 과장을 보태면 \(p\)진수를 통해 합동 방정식을 마치 실변수 방정식처럼 해석적인 직관과 기술을 사용하여 공부할 수 있도록 한다. 어떻게 보면 단순히 ‘언어’를 바꾸는 것이지만, 그 효과로 정수·유리수해에 관한 연구에 새로운 관점과 기술을 열 수 있게 된다. 여기에 관해서는 다음 글에서 자세히 이야기하도록 하자.

20세기 후반에 들어서는 \(p\)진수가 대수적 정수론의 여러 분야에 사용되기 시작하여, 지금은 그 사례를 일일이 나열하는 것이 불가능하게 되었다. 단순히 대수적인 영역에 국한하지 않고 \(p\)진 기하 혹은 또한 \(p\)진 함수에 대한 미분방정식 이론도 다양한 정수론에의 응용을 위한 연구가 여전히 진행되고 있으며, 2018년에는 페터 숄체^P.Scholze가 \(p\)진 기하 이론을 진전시킨 공로로 필즈상을 수상하기까지 하였다. 본 연재에서는 이런 전문적인 내용을 다루기에는 다소 무리가 있지만, 어떤 \(p\)진 이론이 활발하게 연구되고 있는지에 대한 ‘샘플’을 단편적으로나마 제시하고자 한다.