P-ADIC ANALYSIS AND GEOMETRY
Solving equations via p-adic numbers, PART I
이번 연재에서는 ‘\(p\)진수’라는 수 체계에 기반한 해석과 기하를 소개하고자 한다. 실수나 복소수처럼 \(p\)진수 위에서도 ‘자연스러운’ 해석과 기하 이론을 전개할 수 있고, 그 결과가 정수론에 유용하게 쓰이는 반면, 실수와 복소수와는 다른 생소한 현상도 많이 나타난다. 이번 연재를 통해 \(p\)진수의 해석과 기하의 여러 측면을 소개하고, 정수론에서 \(p\)진수의 유용성을 보여주고자 한다. 이번 글에서는 앞서 소개한 \(p\)진수에서 일변수 이차방정식을 풀어보자.
***
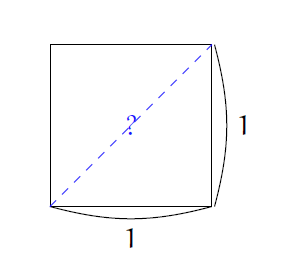
잠시 시계를 과거로 돌려 실수, 무리수, 제곱근의 존재는 모두 잊고 오직 유리수만 알고 있다고 가정해보자. 이제 우리 눈앞에 각 변의 길이가 1인 정사각형이 있을 때, 대각선의 길이를 오차 없이 정확하게 구하고자 한다.([그림1] 참조)
독자들은 모두 훌륭하기에 피타고라스 정리를 어떻게 도출해서 대각선의 길이 \(x\)가 아래 방정식을 만족함을 보일 수 있을 것이다.
\[x^2 = 2.\]그런데 여기에서 좀 곤란해진다. 위 방정식을 오차 없이 정확하게 만족하는 ‘수’를 도무지 찾을 수 없다. (우리는 오직 유리수만 알고 있다고 가정한다.) 미래에서 온 ‘수학의 신’의 전령이 \(x^2 = 2\)를 만족하는 ‘수’는 존재하지 않는다고 어디선가 속삭이는 듯하다.
뉴턴 방법Newton’s method
피타고라스 정리까지 증명했는데, 여기에서 포기하기는 너무 아깝다. 그래서 어떻게든 \(x^2 = 2\)를 풀어보고자 한다.
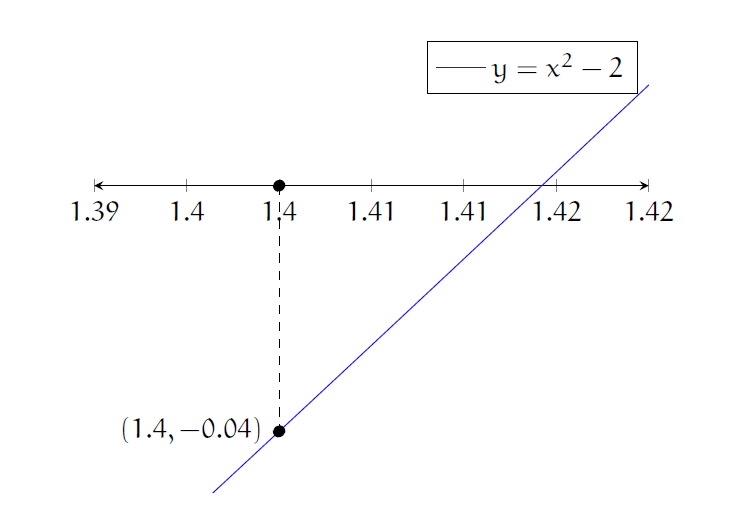
줄자를 가져와서 대각선의 길이를 재보자. 아마 길이가 \(1.4\) 근처 어딘가인 것 같지만 시력이 나빠 더 세밀한 눈금은 도저히 읽을 수 없다. 그런데 \(x_0=1.4\)를 대입하면
\[
x_0^2 = 1.4^2 = 1.96 \ne 2
\]로 여전히 \(|x_0^2-2|=0.04\)의 오차가 있다. 그러면 이 오차를 어떻게 없앨 수 있을까?
좋은 생각이 있다. 중학교 수학에서 배운 함수의 그래프를 활용하면 어떨까? 우선 \(y=x^2-2\)의 그래프를 그려보자. ([그림2] 참조)
그려보니 그래프가 거의 직선 같아 보인다. 사실 \((1.4,-0.04)\)에서 접선의 방정식과 같은 좌표에 겹쳐서 그리면 웬만큼 확대하기 전에는 완전히 겹쳐 보인다. 따라서 \(x^2-2=0\)을 풀 수 없다고 가정했으니, \(y=x^2-2\)의 그래프 대신 접선이 \(x\)축과 만나는 점을 계산해 보면
\begin{align}
x\approx \color{red}{x_1} & :=x_0 – \frac{x_0^2-2}{2x_0}\\
\nonumber &=1.4+\frac{0.04}{2.8} \approx 1.41428571428571
\quad \cdots \quad (1)
\end{align}
을 얻는다. 그러면 \(|x_1^2-2|\approx0.000204\)로 \(x_0:=1.4\)보다 훨씬 좋은 근사값을 얻는다. ([그림3] 참조)
이 과정을 무한히 반복하면 \(x^2=2\)를 만족하는 아직까지는 가상의 수에 무한히 가까워지는 수열 \(\{x_0, x_1,\cdots,x_n,\cdots\}\)을 아래와 같은 공식에서 얻는다.
\begin{equation}
x_{n+1} :=x_n – \frac{x_n^2-2}{2x_n} \quad \forall n\geqslant0.
\quad \cdots \quad (2)
\end{equation}
이제 실수의 정의를 다시 받아들이고 제곱근 \(\sqrt 2\)이 잘 정의되었다고 하면, 위의 수열은 \(\sqrt 2\)로 수렴하는 코시 수열Cauchy sequence이 된다.
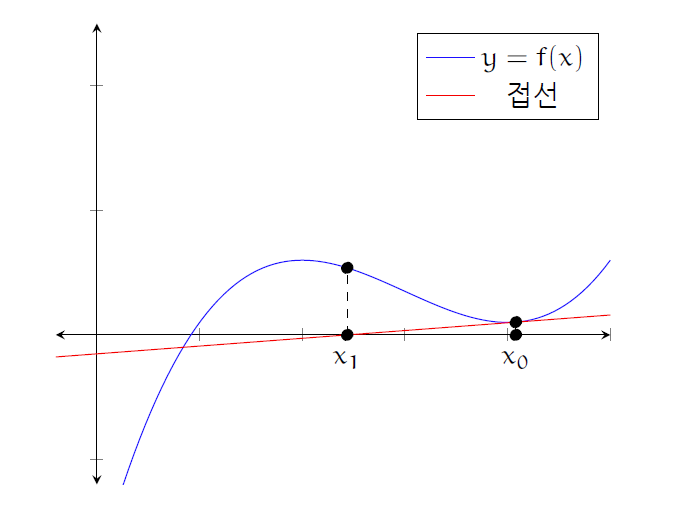
가령 \(f(x) = x^2-2\)같은 주어진 실변수 함수 \(f(x)\)에 대해서 \(f(x) = 0\)의 실수해를 위와 같이 접선의 방정식을 사용하여 유리수 근사하는 방법을 뉴턴 방법Newton’s method이라고 한다. ([그림4] 참조)
물론 뉴턴 방법이 항상 잘 작동하는 것은 아니다. 함수 \(y=f(x)\)가 초기값 \(x_0\) 근처에서 얌전하게 행동해야만 뉴턴 방법이 잘 작동한다. 예를 들어 \(y=f(x)\)가 다항식 같이 충분히 좋은 함수라고 했을 때, 초기값 \(x_0\)에서 접선의 기울기 \(f'(x_0)\)가 너무 \(0\)에 가까우면 뉴턴 방법에 문제가 생길 수 있다. ([그림5] 참조)
\(p\)진수 제곱근을 찾아서…
다시 본론으로 돌아가서 \(x^2=2\)의 해가 유리수에서는 존재하지 않지만1 실수에서는 존재한다. 그러면 실수 대신 어떤 소수 \(p\)를 고정하고 \(p\)진수에서 \(x^2=2\)의 해를 찾을 수 있을까?
구체적인 예를 살펴보자. 소수 \(p\)를 \(7\)로 고정하고
\[
x^2 = 2
\]의 해를 \(7\)진수에서 찾아보자. 흥미롭게도 뉴턴 방법과 유사한 기술(!?!?!?)로 아래와 같이 \(\alpha\)를 \(7\)진 절대값으로 근사하는 유리수의 수열 \(\{\alpha_0,\alpha_1,\cdots\}\)을 만들 수 있다.
먼저 \(\alpha_0^2\)가 \(7\)진 절대값에 대해 적당히 \(2\)에 가까운 초기값 \(\alpha_0\)를 찾아보자. 가령
\[
\alpha_0:= 3
\]으로 두면
\begin{equation}
\color{red}{|\alpha_0^2-2|_7} \color{black}{ = |9-2|_7 = |7|_7 = 7^{-1}} \color{red}{<1}
\quad \cdots \quad (3)
\end{equation}
이 된다.
이제 본격적으로 뉴턴 방법을 쓸 차례다. 여기서 잠깐! \(7\)진수에도 미분이 가능할까? \(7\)진수에서 함수의 그래프에서 접선을 어떻게 생각해야 할까? … 우선 그런 거 생각하지 말고 그냥 우리가 알고 있는 공식에 대입해 보자. 어차피 입시 문제 풀 때 무작정 공식 대입하는 거 많이 해 보지 않았나…
뉴턴 방법에 따르면 \(x^2=2\)의 근사해 \(\alpha_n\)가 주어졌을 때
\[\alpha_{n+1}:= \alpha_n – \frac{\alpha_n^2-2}{2\alpha_n}
\quad \cdots \quad (2)
\]
으로 \(\alpha_{n+1}\)을 정의한다. 이 공식에 그냥 무작정 대입해 보자.
\begin{equation}
\begin{aligned}
\alpha_0 & = 3\\
\nonumber\alpha_1 & = \alpha_0 – \frac{\alpha_0^2-2}{2\alpha_0} = 3 – \frac{1}{6}\cdot 7\\
\nonumber\alpha_2 & = \alpha_1 – \frac{\alpha_1^2-2}{2\alpha_1} =3 – \frac{1}{6}\cdot 7 + \frac{1}{22}\cdot 7^2\\
\nonumber&\vdots
\end{aligned}\quad \cdots \quad (4)
\end{equation}
어랏! 뭔가 \(7\)진 절대값에 대해 수렴하는 것 같아 보인다. 사실
\begin{equation}
\begin{aligned}
|\alpha_1-\alpha_0|_7 & = \left |- \frac{1}{6}\cdot 7\right |_7 = 7^{-1}\\
\nonumber|\alpha_2-\alpha_1|_7 & = \left | \frac{1}{22}\cdot 7^2\right |_7 = 7^{-2}\\
\nonumber&\vdots\\
\nonumber|\alpha_n-\alpha_{n-1}|_7 &= 7^{-n}\\
\nonumber&\vdots
\end{aligned}\quad \cdots \quad (5)
\end{equation}
이 됨을 보일 수 있다. 따라서 이전글 “\(p\)진 해석과 기하: \(p\)진수에 대한 소개”에서 설명한 것처럼 수열 \(\{\alpha_n\}\)은 어떤 \(7\)진수 \(\alpha\)로 수렴한다.2
아직 뭔가 미심쩍은 독자가 있을지도 모르겠다. 그래서 \(\{\alpha_n\}\)의 극한값 \(\alpha\)를 더 구체적으로 적어보자. 먼저 \(7\)진수 \(\beta=\sum_{n=-N}^{\infty}b_n\cdot7^n\)에 대해
\[
\beta = \sum_{n=-N}^{r-1}b_n\cdot7^n+ O(7^r)
\]라고 표기하자. (즉 \(O(7^r)\)은 \( 7^r\)의 \(7\)진 절대값 만큼의 오차를 허용한다는 의미이다.3) 그러면
\begin{equation}
\begin{aligned}
\alpha_0 & = 3\\
\nonumber\alpha_1 & = 3 – \frac{1}{6}\cdot 7 = 3 +1\cdot 7 + O(7^2)\\
\nonumber\alpha_2 & = 3 – \frac{1}{6}\cdot 7 + \frac{1}{22}\cdot 7^2 = 3 +1\cdot 7 + 2\cdot 7^2 + O(7^3) \\
\nonumber&\vdots
\end{aligned}\quad \cdots \quad (6)
\end{equation}
으로 쓸 수 있으며, 계속하면 \(\alpha\)의 \(7\)진법 전개를 얻을 수 있다.
이상 \(x^2=2\)의 \(7\)진수해 \(\alpha\)를 얻어냈다. 하지만 초기값 \(\alpha_0\)를 다른 수로 고르면 어떤 일이 생길까? 초기값 \(\beta_0=4\)를 생각하면
\[
|\beta_0^2-2|_7 = |14|_7 = 7^{-1}<1
\]이 되며, 위의 ‘뉴턴 방법’을 반복하여 얻는 수열 \(\{\beta_n\}\) 역시 \(7\)진수로 수렴한다. 다만 이 수열의 극한값은 \(-\alpha\)가 됨을 확인할 수 있다. (사실 실수의 뉴턴 방법에서도 초기값을 \(y_0 = -1.4\)로 두면 \(-\sqrt 2\)를 근사하는 수열을 얻는다.)
그렇다면
“모든 소수 \(p\)에 대해 \(x^2=2\)의 \(p\)진수 해가 존재하는가?”
라는 질문을 던질 수 있다. 하지만 아쉽게도 정답은 “No”다. 예를 들어 \(p\)를 \(3\)이나 \(5\)로 두면, 모든 정수 (심지어는 모든 유리수) \(a\)에 대해서도
\[
|a^2-2|_p\geqslant 1
\]이 되어 \(p\)진 뉴턴 방법에 대입할 초기값을 찾을 수가 없다. 실제로도 방정식 \(x^2=2\)의 \(3\)진수해나 \(5\)진수해는 존재하지 않는다.
또한 \(p=2\)로 두고 \(x^2=2\)의 \(2\)진수해 \(\alpha\)가 존재한다고 가정하면, \(2\)진 절대값의 성질에 의해 다음과 같은 식을 얻는다.
\begin{equation}
\left (|\alpha|_2\right ) ^2 = |\alpha^2|_2 = |2|_2 = 2^{-1}.
\quad \cdots \quad (7)
\end{equation}
따라서 \(|\alpha|_2 = 2^{-1/2}\)임을 얻는다. 하지만 어떤 \(2\)진수에 대해서도 절대값은 \(2\)의 정수 거듭제곱만 허용되며 \(2^{-1/2}\)은 \(2\)진수의 절대값으로 허용되지 않는다. 따라서 \(x^2=2\)의 \(2\)진수해는 존재하지 않는다.
여기에 흥미로운 따름 정리 하나를 소개하고자 한다.
정리. \(x^2=2\)의 유리수해는 존재하지 않는다.
Proof. 유리수는 실수와 임의의 소수 \(p\)에 대해 \(p\)진수에 속해 있기 때문에, \(x^2=2\)의 유리수해가 존재한다면 \(x^2=2\)의 실수해와 \(p\)진수해가 항상 존재해야 한다. 하지만 \(p=2,3,5\)처럼 \(x^2=2\)의 \(p\)진수해가 존재하지 않는 소수 \(p\)가 존재한다. 따라서 \(x^2=2\)의 유리수해는 존재하지 않는다.
\(p\)진 제곱근
\(2\)의 제곱근의 경우에서 살펴보았듯이, 유리수에서는 제곱근이 존재하지 않지만 실수에서는 제곱근이 존재하는 경우가 많다. 가령:
보조정리. \(0\) 이상의 모든 실수 \(r\)에 대해 제곱근 \(\sqrt{r}\)이 실수에서 잘 정의된다. 따라서 \(0\) 이상의 유리수의 제곱근은 실수에서 항상 정의된다.
그러면 소수 \(p\)를 고정했을 때, \(p\)진수에서의 제곱근은 언제 존재할까?4
임의의 \(p\)진수 \(\beta\)에 대해 \(|\beta|_p = p^{-N}\)이라고 하고 \(\mathfrak{u}:=\beta\cdot p^{-N}\)이라고 두면, \(\mathfrak{u}\)의 \(p\)진 절대값은
\[
|\mathfrak{u}|_p = |\beta\cdot p^{-N}|_p = |\beta|_p\cdot |p^{-N}|_p = p^{-N}\cdot p^{N}=1
\]임을 얻는다. 즉 임의의 \(p\)진수 \(\beta\)는
\begin{equation}
\beta = \mathfrak{u}\cdot p^N, \quad \text{여기에서 }|\mathfrak{u}|_p=1
\quad \cdots \quad (8)
\end{equation}
로 유일하게 쓸 수 있다.
이제 수식(8)의 형태로 쓰인 임의의 \(p\)진수 \(\beta=\mathfrak{u}\cdot p^N\)가 언제 다른 \(p\)진수의 제곱으로 쓰일 수 있는지 판별하도록 하자.
- 먼저 \(\alpha^2 = \beta\)라면 수식(7)과 비슷한 논리로
\[
|\alpha|_p = p^{-N/2}
\]가 되어 \(N\)이 짝수여야 한다. - 만약 \(N\)이 짝수라면, \(\beta\)가 어떤 \(\)진수의 제곱일 필요충분 조건은 \(\mathfrak{u} = \beta\cdot p^{-N}\)이 \(p\)진수의 제곱이 되는 것이다.
따라서 절대값이 \(1\)인 \(p\)진수 \(\mathfrak{u}\)에 대해 \(x^2=\mathfrak{u}\)의 \(p\)진수해가 언제 존재하는지만 판별하는 것이 남았다. 먼저 \(|\mathfrak{u}|_p=1\)이라는 가정 때문에 \(\mathfrak{u}\)는 아래와 같은 \(p\)진 전개를 갖는다.
\begin{equation}
\mathfrak{u} = u_{0} + u_{1}\cdot p+ u_2\cdot p^2+\cdots.
\quad \cdots \quad (9)
\end{equation}
여기에서 \(u_0, u_1, u_2,\cdots\)는 \(0\)부터 \(p-1\)까지의 정수이며 \(u_0\)은 \(0\)이 될 수 없다.
정리. 먼저 소수 \(p\)가 \(2\)가 아니라고 가정하자. 절대값이 \(1\)인 \(p\)진수 \(\mathfrak{u}\)를 수식(9)와 같이 표현하면, 방정식 \(x^2=\mathfrak{u}\)가 \(p\)진수해를 가질 필요충분조건은 \(u_0\)가 \(p\)에 대한 제곱 잉여quadratic residue인 것이다. 즉 합동방정식
\begin{equation}
x^2 \equiv u_0\mod{p}
\quad \cdots \quad (10)
\end{equation}
의 해가 존재하는 것과 \(x^2=\mathfrak{u}\)가 \(p\)진수해가 존재하는 것은 동치이다.
\(p=2\)인 경우, 방정식 \(x^2=\mathfrak{u}\)가 \(2\)진수해를 가질 필요충분조건은
\begin{equation}\label{eq:initial-value3}
|\mathfrak{u} – 1|_2 \leqslant 2^{-3}
\quad \cdots \quad (11)
\end{equation}
을 만족하는 것이다.
Proof. 증명의 아이디어는 \(x^2=2\)의 \(7\)진수해를 구하는 방법과 거의 동일하다. 편의상 \(p\)를 \(2\)가 아닌 소수인 경우만 생각하자.5 먼저 \(u_0\)가 \(p\)에 대한 제곱 잉여라고 하면, 어떤 자연수 \(a_0\)가 있어서
\begin{equation}
a_0^2\equiv u_0\mod{p},\quad\text{ 즉 } \color{red}{|a_0^2-\mathfrak{u}|_p = p^{-1}<1}
\quad \cdots \quad (12)
\end{equation}
임을 보일 수 있다. 따라서 \(a_0\)를 초기값으로 하여 ‘\(p\)진 뉴턴 방법’을 적용하면 방정식 \(x^2=\mathfrak{u}\)의 \(p\)진수해에 수렴하는 수열을 만들 수 있다. 반대로 \(u_0\)가 \(p\)에 대한 제곱 잉여가 아니라고 하면 ‘\(p\)진 뉴턴 방법’을 적용할 초기값을 찾을 수가 없다.
정리를 활용하는 몇 가지 예를 들어 보자. 먼저 \(x^2=2\)의 \(p\)진수해의 존재성을 살펴보면, \(2\)를 제외한 소수 \(p\)에 대해 \(|2|_p=1\)이므로 위의 정리에 따라 어느 소수 \(p\)에 대해 \(2\)가 제곱 잉여인지 판별하면 된다. 이제 가우스의 이차 상호 법칙quadratic reciprocity law의 제2 보충 법칙에 의해서, \(2\)가 \(p\)에 대한 제곱 잉여일 필요충분조건은
\[
p \equiv \pm 1\mod 8
\]이다. 따라서 \(p=7,17,23,31,41,\cdots\)이면 \(x^2=2\)의 \(p\)진수해가 존재하고, \(p=(2,)3,5,11,13,19,\cdots\)이면 \(x^2=2\)의 \(p\)진수해가 존재하지 않는다.
다른 예로 \(x^2=-1\)의 \(p\)진수해의 존재성을 살펴보자. (이 방정식은 실수해를 갖지 않는다!) 먼저 모든 소수 \(p\)에 대해 \(|-1|_p=1\)을 만족한다. \(p=2\)인 경우에는
\[
|-1-1|_2 = 2^{-1} > 2^{-3}
\]이 되어, \(\mathfrak{u}=-1\)은 \(x^2=\mathfrak{u}\)이 \(2\)진수해를 가질 필요충분조건(12)를 만족하지 않는다. 다음으로 \(2\)를 제외한 소수 \(p\)에 대해서는 위의 정리에 따라 어느 소수 \(p\)에 대해 \(2\)가 제곱 잉여인지 판별하면 되는데, 그 필요충분조건은 가우스의 이차 상호 법칙quadratic reciprocity law의 제1 보충 법칙에 의해서
\[
p \equiv 1\mod 4
\]로 주어진다. 따라서 \(p=5,13,17,29,37,\cdots\)이면 \(x^2=-1\)의 \(p\)진수해가 존재하고, \(p=2,3,7,11,19,23,\cdots\)이면 \(x^2=-1\)의 \(p\)진수해가 존재하지 않는다.
\(p\)진 뉴턴 방법: aka 헨젤의 보조정리Hensel’s Lemma
앞서 소개한 ‘\(p\)진 뉴턴 방법’은 단지 \(p\)진 제곱근을 구하는 데에만 국한되지 않고 더 일반적인 방정식의 \(p\)진수해를 구하는 데에 활용될 수 있다. 사실 이 결과는 통상적으로 헨젤의 보조정리라고 불린다.
먼저 편의상 \(f(x)\)를 정수 계수의 다항식이라고 하자.6 그러면 교과과정(혹은 미적분학)에서 배운대로 미분 \(f'(x)\)를 생각할 수 있다.
정리(헨젤의 보조정리Hensel’s Lemma). 주어진 정수 계수 다항식 \(f(x)\)에 대해 다음 조건을 만족하는 정수 \(a\)가 있다고 하자.
\begin{equation}
|f(a)|_p < | f'(a) |_p^2.
\quad \cdots \quad (13)
\end{equation}
그러면 방정식 \(f(\alpha)=0\)과 부등식 \(|\alpha-a|_p<| f'(a) |_p\)를 동시에 만족하는 \(p\)진수 \(\alpha\)가 존재한다.7
잠시 실수에 대한 뉴턴 방법에서 직관을 빌려오자. 방정식 \(f(x)=0\)의 실수해를 근사하기 위해 뉴턴 방법을 적용하려면, 초기값 \(x=a\)에서 접선의 기울기 \(f'(a)\)가 너무 작으면 문제가 생긴다.([그림5] 참조) \(p\)진수의 경우에는 수식(13)에서처럼 \(f(a)\)가 \(f'(a)\)에 비해 훨씬 \(0\)에 가까우면 ‘\(p\)진 뉴턴 방법’을 적용하여 \(f(x)=0\)의 \(p\)진수해를 근사하는 수열을 만들 수 있다는 것이 증명의 핵심 아이디어이다.
또한 굳이 사족을 달자면 앞서 \(p\)진 뉴턴 방법’을 적용하기 위한 초기값의 조건으로 주어진 수식들은 모두 (13)의 특수 경우이다. (참조: 수식(3),(12),(11).)
에필로그: 헨젤의 보조정리, 합동식, \(p\)진수
헨젤의 보조정리는 기초 정수론의 관점에서 보면 다음과 같이 해석할 수 있다.
따름정리. 정수 계수 다항식 \(f(x)\)이 주어졌다고 하자. 어떤 정수 \(N\geqslant0\)에 대해서 다음 합동 조건을 만족하는 정수 \(a\)가 있다고 하자.
\begin{align}\label{eq:Hensel-cong}
f(a) &\equiv 0 \mod{p^{2N+1}}\\
\nonumber f'(a) &\not\equiv 0 \mod{p^{N+1}}
\quad \cdots \quad (14)
\end{align}
그러면 방정식 \(f(x)=0\)의 \(p\)진수해가 존재한다.8 이 따름정리 역시 다변수 다항식에도 일반화할 수 있다.
조금 단순화해서 말하면 다항식 방정식의 \(p\)진수해 존재성은 결국 \(p\)의 거듭제곱에 대한 합동해의 존재성과 거의 동치이다.
그렇다면 이런 질문을 품은 독자가 있을지도 모르겠다.
“방정식의 \(p\)진수해를 구하는 문제가 결국 합동방정식을 푸는 것이라면,
왜 굳이 \(p\)진수를 도입해야 하는 이유가 뭘까?”
사실 합동방정식을 정의하고 설명하는 것은 \(p\)진수를 도입하는 것보다 더 적은 노력이 드는 것도 사실이다. 하지만 소수 \(p\)의 거듭제곱에 대한 합동방정식은 직관적으로 다루기 쉽지 않은 것도 사실이다. 예를 들어 \(8=2^3\)에 대한 합동 방정식을 생각해 보면 일차 합동방정식 \[2x\equiv 5 \mod{8}\] 처럼 합동해가 존재하지 않는 경우가 있는가 하면 \[2x\equiv 4 \mod{8}\] 처럼 합동해가 \(x=2,6\) 같이 두 개 이상인 경우도 있다. 합동 이차방정식만 보아도 \[x^2\equiv 1\mod{8}\]의 경우 \(x=1,3,5,7\) 모두 합동해이다. (즉 이차방정식에 4개의 합동해가 존재하게 된다.) 하지만 \(2\)진수의 세계에서는 \(2x=5\)와 \(2x=4\) 모두 유일한 해가 존재하며, \(x^2=1\)의 해는 \(x=\pm1\) 두 개뿐이다. 즉 합동방정식을 \(p\)진수의 틀에 넣으면, 오히려 실수나 복소수 위에서 방정식을 푸는 것처럼 자연스러운 직관을 적용할 수 있다.
합동 방정식의 가장 큰 용도는 방정식의 정수해에 관한 응용일 것이다. 마찬가지로 방정식의 \(p\)진수해를 바라보는 가장 큰 이유는 방정식의 정수해 혹은 유리수해의 존재성을 이해하기 위함이다. 다음글에서는 특정 다변수 이차방정식의 정수해와 유리수해의 존재성을 판별하는데 어떻게 \(p\)진수 이론을 사용할 수 있는지 알아보도록 하겠다.9