P-ADIC ANALYSIS AND GEOMETRY
P-adic geometry, from Tate to Scholze
이번 연재에서는 ‘\(p\)진수’라는 수 체계에 기반한 해석과 기하를 소개하고자 한다. 실수나 복소수처럼 \(p\)진수 위에서도 ‘자연스러운’ 해석과 기하 이론을 전개할 수 있고, 그 결과가 정수론에 유용하게 쓰이는 반면, 실수와 복소수와는 다른 생소한 현상도 많이 나타난다. 이번 연재를 통해 \(p\)진수의 해석과 기하의 여러 측면을 소개하고, 정수론에서 \(p\)진수의 유용성을 보여주고자 한다.
연재의 마지막 편에 해당하는 이번 글에서는 \(p\)진 기하의 기원이 된 ‘테이트 타원 곡선’과 최근 많이 연구되고 있는 숄체의 ‘퍼펙토이드 공간 이론’에 대해 소개하려고 한다.
***
이전 글 “p진 해석과 기하 [5]: \(p\)진수 함수의 세계”에서 \(p\)진 초월함수와 미분방정식을 소개하면서, \(p\)진 미분방정식에 관한 드웍B.Dwork의 선구적인 업적이 \(p\)진 기하 이론의 존재를 강하게 암시한다고 하였다. 이번 글에서는 최근 작고한 정수론의 대가 테이트J.Tate, 1925-2019부터 2018년 필즈상 수상자 숄체P.Scholze에 이르기까지 \(p\)진 기하의 기원과 현재에 관해 살펴보고자 한다.
속이 빈 도넛과복소 원환면complex torus
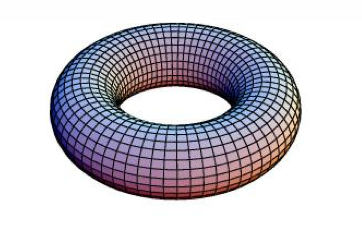
생소한 \(p\)진 기하에 대해 이야기 하기 전에, 먼저 우리에게 좀 더 친숙한 고전적인 기하 이야기로 시작해 보자. 지금까지 본 연재에서 다룬 공간은 원판, 삼각형, 평면 위의 경로처럼 모두 평면에 속해 있었다. 이제 본격적으로 기하를 다루기 위해 평면을 벗어나 아래의 ‘속이 빈 도넛’을 살펴보자.
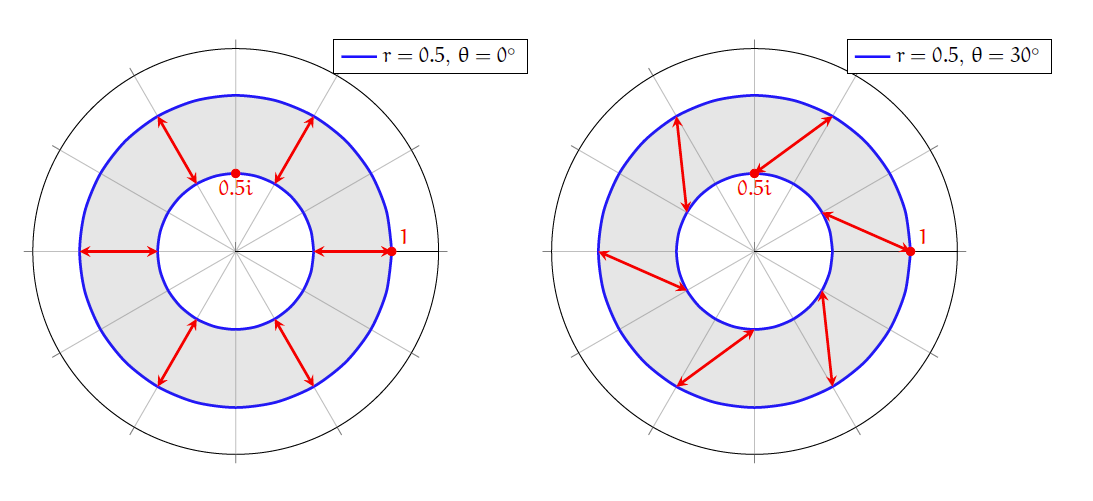
그런데 평면을 벗어나는 공간에서 기하를 다루려면 상상력이 많이 동원되어야 하고, 그림을 그리기에도 뭔가 불편하다. 따라서 조금 반칙적인 기술을 써서, 평면 위의 도형을 적당히 구부리고 늘리고 붙여서 위의 곡면을 만들어 보는 것은 어떨까. 먼저 \(1\)보다 작은 양의 실수 \(r\)과 각도 \(\theta\)를 고정하자. (구체적으론 \(r=0.5, \theta = 30^{\circ}\), 혹은 \(r= e^{-2\pi}, \theta = 0^{\circ}\)로 두어도 좋다.)
반지름 \(1\)인 닫힌 원판에서 반지름 \(r\)인 원판을 도려내어 원환annulus을 만들고, [그림2]처럼 안쪽 원과 바깥쪽 원의 각도를 \(\theta\)만큼 틀어서 붙여 보자. (물론 길이가 다르기 때문에 안쪽 원을 늘려서 붙여야 할 것이다.) 이제 약간의 상상력을 동원하면 속이 빈 도넛을 얻음 수 있음을 알 수 있다.
이제 평면의 점 \((u,v)\)를 복소수 \(w=u+vi\)로 간주하자.1 단순히 포장만 바꾸는 것처럼 보일 수도 있지만, 여기에서 얻을 수 있는 중요한 점이 하나 있다. 바로 복소수는 곱하고 나눌 수 있다는 것이다.
앞에서처럼 \(1\)보다 작은 양수 \(r\)과 각도 \(\theta\)를 고정하고 \(q\)를 아래와 같은 복소수로 두자:
\begin{equation}
q = r\cos\theta +(r\sin\theta)i.
\end{equation}
가령 \(\theta = 0^\circ\)라면, \(q=r\)이 된다.
복소수 \(w\)의 크기 \(|w|\)를 \(0\)부터 \(w\)까지의 거리로 정의하자. 평면 위의 점을 복소수로 이해하면, 앞서 설명한 속 빈 도넛을 만드는 방법을 아래와 같이 이해할 수 있다.

위의 오른쪽 행에서 설명한 방법으로 얻을 수 있는 곡면을 복소 원환면complex torus이라고 한다.
복소 원환면과 복소 타원곡선
조금 놀라운 사실은 위처럼 정의한 복소 원환면을 어떤 이변수 삼차방정식의 복소해의 집합으로 자연스럽게 이해할 수 있다는 점이다. 이는 19세기에 알려진 결과로, 바이어슈트라스K.Weierstrass는 상당히 구체적인 공식까지 제시하였다. 비록 공식이 조금 복잡한 편이지만, 구체적인 논의를 위해 공식을 자세히 써 보도록 하겠다.
식(1)처럼 복소수 \(q\)를 고정하고,
복소수 \(w\)를 변수로 갖는 함수 \(x_q(w), y_q(w)\)를 아래와 같이 정의하자:
\begin{align}
x_q(w) & := \sum_{m=-\infty}^{\infty}\frac{wq^m}{(1-wq^m)^2} -2\sum_{n=1}^{\infty}\frac{q^n}{(1-q^n)^2},\\y_q(w) & := \sum_{m=-\infty}^{\infty}\frac{(wq^m)^2}{(1-wq^m)^3} + \sum_{n=1}^{\infty}\frac{q^n}{(1-q^n)^2}.\notag
\end{align}
크기가 \(r=|q|\)과 \(1\) 사이의 복소수 \(w\)에 대해서 위 무한급수는 \(w\ne1,q\)인 경우에 수렴함을 보일 수 있고2, 또한 \(x_q(qw) = x_q(w), y_q(qw) = y_q(w)\)임을 정의에서 쉽게 확인할 수 있다.
따라서 크기 \(1\)인 복소수 \(w\)와 \(q\cdot w\)를 붙여서 얻어진 복소 원환면을 \(X_q\)라고 두면, \(x_q, y_q\)는 \(X_q\)의 한 점을 제외한 모든 점에서 복소수를 대응시키는 함수로 볼 수 있다. (참고로 복소수 \(1\)과 \(q\)는 \(X_q\)에서 같은 점을 주며, 이 점을 \(e\in X_q\)라고 두자. 그러면 \(x_q, y_q\)는 \(e\)를 제외한 \(X_q\)의 모든 점에서 정의할 수 있다.)
마지막으로 \(0<|q|<1\)을 만족하는 복소수 \(q\)에 대해서 아래와 같이 수렴하는 무한급수로 복소수 \(h_2(q), h_3(q)\)를 정의하자:
\begin{align}
h_2(q) & := \sum_{n=1}^{\infty}\frac{n^3q^n}{1-q^n},\\h_3(q) & := -\frac{1}{12} \sum_{n=1}^{\infty}\frac{(5n^3+7n^5)q^n}{1-q^n}.\notag
\end{align}
정리1 [바이어슈트라스Weierstrass] 위와 같이 복소수 \(q\)를 고정하자. 그러면 \(|q|\leqslant |w| \leqslant1\)을 만족하며 \(1\)과 \(q\)를 제외한 복소수 \(w\)에 대해 \((x,y)=(x_q(w), y_q(w))\)는 아래 삼차방정식을 만족한다.
\begin{equation}
y^{2} + xy = x^3 – h_2(q)x – h_3(q).
\end{equation}
더 나아가 \(w\)를 \((x_q(w), y_q(w))\)로 보내는 함수가 아래와 같은 일대일 대응을 유도한다.
\begin{equation}
{ X }_{ q }\setminus \{ e\} \longleftrightarrow \text{방정식4를 만족하는 복소수쌍 \((x,y)\)}
\end{equation}
만약 \(x_q(w), y_q(w), h_2(q),h_3(q)\)의 공식을 알고 있다면, 복소수쌍 \((x_q(w), y_q(w))\)이 방정식(4)를 만족함을 보이는 것은 어렵지 않다. 그리고(5)가 일대일 대응임은 학부과정의 복소해석에서 도출할 수 있다. 따라서 증명의 핵심은 \(x_q(w), y_q(w), h_2(q),h_3(q)\)의 공식을 찾아내는 것인데, 이 공식을 제공하는 것이 소위 타원함수elliptic functions 및 세타함수theta functions 이론이다. 특히 \(x_q(w)\)는 바이어슈트라스 \(\wp\)함수의 변형으로 이해할 수 있다.
위 정리의 중요성을 설명하자면, (5)의 좌변인 한 점을 뺀 복소 원환면은 기하적으로 다루기 쉬운 형태의 곡면인 반면, 우변은 대수적으로 다루기 쉬운 형태이다. 또한 계수 \(h_2(q), h_3(q)\)가 정수 혹은 유리수인 경우에는 소위 유리 타원곡선이라고 부르는, 정수론에서 중요하게 다뤄지는 공간이 된다. 바이어슈트라스 정리를 통해, 복소 원환면에 기하적 방법론과 대수적 방법론을 모두 적용할 수 있게 된다.
테이트J.Tate의 \(p\)진 바이어슈트라스 이론
이전 글 “p진 해석과 기하 [5]: \(p\)진수 함수의 세계”에서 지수함수, 로그함수, 초기하함수처럼, 테일러 전개가 유리수 계수를 가지며 변수에 실수·복소수 대신 \(p\)진수를 대입할 때에도 양의 수렴반경을 가지는 예시를 살펴보았다. 테이트의 놀라운 관찰은 비슷한 현상이 위의 바이어슈트라스 정리에 등장하는 함수와 상수에도 나타난다는 것을 발견한 것이다. 즉 테이트는 \(q\)를 적당한 유리수 혹은 \(p\)진수로 고르면, (2),(3)에서 주어진 \(x_q(w),y_q(w), h_2(q), h_3(q)\)의 공식이 \(p\)진수에서도 성립하며 바이어슈트라스 정리와 비슷한 결과를 얻을 수 있음을 발견했다.
보조정리2 [테이트, 1950년대] 절대값이 \(1\)보다 작은 양수인 \(p\)진수 \(q\)를 고정하자. 그러면 복소수의 경우와 같은 공식(3)에 의해 \(p\)진수 \(h_2(q), h_3(q)\)이 잘 정의된다.
만약 \(w\)가 \(|q|_p\leqslant |w|_p\leqslant 1\)을 만족하고 \(w\ne 1,q\)라고 하면 복소수의 경우와 같은 공식(2)에 의해 \(x_q(w), y_q(w)\)가 잘 정의되며, 아래 등식이 성립한다.
\begin{align*}
& x_q(qw) = x_q(w) \quad \& \quad y_q(qw) = y_q(w),\\\text{(4)…}\qquad &y_q(w)^{2} + x_q(w)y_q(w) = x_q(w)^3 – h_2(q)x_q – h_3(q).
\end{align*}
증명은 사실 어렵지 않다. 예를 들어 (2)에서 정의된 \(x_q(w)\)를 다시 살펴보자.
\(x_q(w) := \sum_{m=0}^{\infty}\frac{wq^m}{(1-wq^m)^2} + \sum_{m=1}^{\infty}\frac{w^{-1}q^m}{(1-w^{-1}q^m)^2} -2\sum_{n=1}^{\infty}\frac{q^n}{(1-q^n)^2}.\)
비록 \(w\)에 대한 테일러 전개 꼴로 쓰이진 않았지만, 만약 \(q\)가 유리수라면 변수 \(w\)에 \(p\)진수를 대입하여 위 급수가 \(p\)진수에서 수렴하는지 물을 수 있다. 여기에서 \(q\)의 \(p\)진 절대값 \(|q|_p\)이 \(1\)보다 작고 \(w\)를 분모가 \(0\)이 되지 않게 하는 \(p\)진수로 고르면, 위 식에 등장하는 세 개의 무한급수 모두 \(p\)진수에서 수렴함을 쉽게 알 수 있다.3 사실 \(q\)에 유리수 대신 절대값이 \(1\)보다 작은 임의의 \(p\)진수를 대입하여도 같은 성질을 도출할 수 있으며, 비슷한 방법으로 \(y_q(w), h_2(q), h_3(q)\) 역시 \(p\)진수에서 잘 정의됨을 알 수 있다.
이제 복소 원환면을 만드는 방법대로 \(p\)진 원환면\(p\)-adic torus을 만들어 보자. 먼저 \(p\)진 절대값이 \(1\)보다 작은 양수인 \(p\)진수 \(q\)를 고정하고, \(p\)진 절대값을 \(r:=|q|_p\)로 두자. 그리고 \(p\)진 절대값이 \(r\)과 \(1\) 사이인 \(p\)진수가 만드는 원환을 생각하자. 그리고 바깥 경계인 \(p\)진 절대값 \(1\)인 \(p\)진수 \(w\)를 \(qw\)와 붙여서 만든 공간을 \(p\)진 원환면이라고 부르고 \(X_q\)라고 두자. 그러면 \(1\)과 \(q\)는 \(X_q\)에서 같은 점 \(e\)에 대응되며, 보조정리2에 의해서 \(x_q(w)\)와 \(y_q(w)\)는 \(X_q\setminus\{e\}\)의 함수로 볼 수 있다.
정리3 [테이트, 1950년대] 절대값이 \(1\)보다 작은 양수인 \(p\)진수 \(q\)를 고정하자. 그러면 \(p\)진수 \(w\)를 \((x_q(w), y_q(w))\)로 보내는 함수가 아래와 같은 일대일 대응을 유도한다.
\begin{equation}
{ X }_{ q }\setminus \{ e\} \longleftrightarrow \text{방정식4를 만족하는 \(p\)진수쌍 \((x,y)\)}
\end{equation}
이 결과는 다항식 방정식 \(y^2+xy=x^3-h_2(q)x-h_3(q)\)의 \(p\)진수해를 \(p\)진 원환면의 점에 구체적으로 대응시키는, 정수론에서 정말 유용한 정리이다. 증명의 핵심 역시 바이어슈트라스의 정리(정리1)처럼 올바른 공식을 찾는 것이다.4
테이트의 정리와 \(p\)진 기하의 태동
이전 글 “\(p\)진 해석과 기하 [5]: \(p\)진 함수의 세계”에서도 언급했지만, 실변수 혹은 복소변수 함수에 \(p\)진수를 대입하여 \(p\)진 함수를 얻어낼 수 있다면, 이를 가능하게 하는 ‘원리’가 있는 것이 보통이다. 따라서 테이트는 아래와 같은 질문을 던졌던 것 같다.
질문4. 정리3에 더 깊은 의미를 부여하는 \(p\)진 기하 이론이 있는가?
질문의 맥락을 이해하기 위해 잠시 복소 원환면으로 돌아가 보자. 복소 원환면은 소위 복소기하complex geometry라고 부르는 이론에서 다루는 범주에 있는 곡면으로, 복소기하의 맥락에서 바이어슈트라스 정리(정리1)에 더 깊은 의미를 부여할 수 있다. 반면에 \(p\)진 원환면이 속하는 기하학의 범주는 50년대에 존재하지 않았다. 따라서 복소 원환면의 경우처럼 테이트의 정리(정리3)에 더 깊은 의미를 부여하는 \(p\)진 기하 이론이 있을지 의문을 가질 수 있을 것이다.
1959년 테이트는 대수기하의 대가인 그로텐디크A.Grothendieck에게 편지로 정리3과 관련 공식들을 설명하고 위의 내용을 질문하였다. 그로텐디크는 주어진 이론을 추상화하여 올바른 ‘생각의 틀’을 만들어내는 데 천재적이었기 때문에, 테이트는 그로텐디크에게 \(p\)진 원환면 등을 포함하는 일반적인 \(p\)진 기하 이론에 대한 어떤 혜안을 기대했을지도 모르겠다.
하지만 그로텐디크는 질문4에 대해 회의적이었던 것 같다. 1959년 8월 18일, 그로텐디크는 세르J.P.Serre에게 보낸 편지에서 테이트의 편지를 언급하고는 “정리3과 같은 결과가 \(p\)진 기하 이론의 존재를 암시하는지 전혀 이해할 수 없다”고 하고는, 테이트의 정리3에 대해선 그저 “구체적이고 지저분한 공식”으로 치부하였다.5
반세기 이상 지난 지금 당시 그로텐디크의 반응을 비판하기는 쉽겠지만, 뒤집어 말하면 그로텐디크가 그러한 반응을 보일 만큼 \(p\)진 기하 이론의 존재가 기적적이라고도 말할 수 있다.
결국 1960년대 테이트는 강체기하rigid geometry고 불리는 \(p\)진 기하이론을 개발하였다. 공교롭게도 \(p\)진 기하 이론의 기초에 그로텐디크 위상Grothendieck topology을 포함한 그로텐디크의 아이디어가 중심적인 역할을 한다. 본 연재에서 이를 자세히 설명하기엔 무리가 있지만 큰 아이디어는 다음과 같다. \(p\)진수가 만드는 공간 자체는 너무 특이한 성질이 많기 때문에 기하학을 정립하기에 여러모로 어려움이 많다. 따라서 테이트의 아이디어는 공간 대신, 혹은 공간을 잊어버리더라도, 공간에 정의된 함수만 가지고 기하학을 할 수 있다는 그로텐디크의 철학을 사용하여 \(p\)진 기하 이론을 세우는 것이다. 즉 \(p\)진 기하에서 다룰 ‘\(p\)진 다양체’를 공간으로 직접 정의하는 대신, 그 공간에 어떤 함수가 정의되어야 하는지를 정하는 방법으로 ‘\(p\)진 다양체’를 정의한다.
테이트의 \(p\)진 기하이론은 초기 단계에서부터 대수적 정수론 및 산술기하arithmetic geometry에서 기술적인 도구로 유용하게 쓰이기 시작하였다. 특히 지난 연재글에서 다루었던 드웍B.Dwork의 \(p\)진 미분방정식에 관한 연구와 함께 보형 곡선modular curves 및 보형 형식modular forms의 산술적 연구에 큰 공헌을 하였고, 이 결과들은 직간접적으로 와일즈A.Wiles의 페르마 마지막 정리 증명에 공헌하기도 하였다.
테이트에서 숄체P.Scholze까지
요약하자면 테이트의 \(p\)진 기하이론은 존재 자체가 놀라운 이론인 동시에, 정수론에의 응용 측면에서도 큰 성공을 거두었다. 하지만 성공적인 수학 이론이기에 더더욱 자연스럽고 강력한 이론으로 다듬어가는 과정이 필요했으며, 테이트 이후에도 많은 대가들이 \(p\)진 기하이론을 발전시켜 왔다.
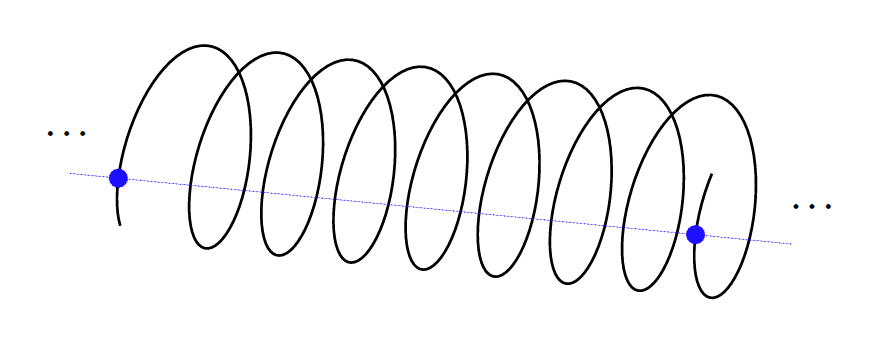
2011년 당시 박사과정 대학원생이었던 숄체는 학위연구에 필요한 도구로 퍼펙토이드 공간perfectoid spaces이라는 \(p\)진 공간을 고안해 냈다. 정확한 정의는 본 연재글의 범위를 벗어나지만, 굳이 그림을 그리자면 \(p\)진 기하에서 무한 솔레노이드의 곱과 비슷하게 생각할 수 있다. ([그림3] 참조)
원래 숄체가 의도했던 바는 Weight-Monodromy Conjecture라는 산술기하의 난제를 공략하는 도구로 활용하기 위함이었고, 이 측면에서 ‘절반의 성공’을 거두었지만, 숄체 자신을 포함한 여러 대가들은 퍼펙토이드 공간이 \(p\)진 기하에서 훨씬 근본적인 역할을 하는 공간임을 금방 알아차렸다.
즉 \(p\)진 기하에서 퍼펙토이드 공간은 일종의 ‘기본 레고 블록’ 같은 것으로, 퍼펙토이드라는 레고 블록을 잘 조립하여 ‘\(p\)진 다양체’라는 흥미로운 공간들을 만들어낸다는 관점으로 \(p\)진 기하를 재해석할 수 있다. 마치 \(p\)진 원환을 적당히 붙여 \(p\)진 원환면 \(X_q\)를 만들듯이, \(p\)진 기하에서 다루는 공간들은 퍼펙토이드 공간을 적당히 자르고 붙여서 만들어낸 공간으로 이해하는 접근이다. 이 관점에 따르면 \(p\)진 기하의 기술적으로 까다로운 여러 문제를 퍼펙토이드 공간에 관한 문제로 귀결시킨 후 해결할 수 있다. 숄체는 이 전략으로 정수론 학계를 흥분시키는 중요한 결과들을 하나씩 발표하며 2018년 필즈상을 수상하였다.6
숄체는 필즈상 수상 이후에도 퍼펙토이드의 도입에서 시작된 이론을 더 깊이 발전시켜 나가면서 정수론에 중요한 난제들을 하나하나 공략하고 있다. 예를 들어 ‘타원곡선’이라고 부르는 이변수 삼차방정식의 소수 \(p\)에 대한 합동근 개수의 균등분포에 관한 사토-테이트 가설Sato-Tate Conjecture에 관해 9명의 공저자와의 공동연구, 그리고 최근 국소 랭글랜즈 상관관계Local Langlands Correspondence 7에 관한 파르그L.Fargues와의 공동연구 등 숄체는 필즈상 수상업적을 뛰어넘는 연구를 계속 진행해 오고 있다.
맺음말
“\(p\)진 해석과 기하”에 관한 연재를 마무리하기에 앞서 전체 내용을 간단히 요약해 보고자 한다.
1편 “수를 크기를 재는 여러 방법”에서는 우리가 항상 사용하는 유리수의 ‘자연스러운 절대값’을 공리화하면서 다른 공리와 독립적인 아르키메데스 공리를 추출해 내고, 아르키메데스 공리를 만족하지 않는 절대값으로 \(p\)진 절대값을 소개하였다. 비유하자면 유클리드 기하를 평행선 공리에서 해방시키는 순간 기하의 새로운 지평이 열리는 것처럼, 비非아르키메데스 절대값인 \(p\)진 절대값이 적어도 정수론의 관점에서 흥미로운 해석과 새로운 기하의 지평을 열지 않을까 하는 희망적인 기대를 할 수 있다.
2편 “\(p\)진수에 대한 소개”에서는 \(p\)진 절대값이 만족하는 특이한 성질들을 소개하였다. 예를 들어 \(p\)진 원판에서는 모든 점이 중심이며, 모든 삼각형이 뾰족한 이등변삼각형이라는 점을 보았다. 비록 현실세계의 직관에 어긋나는 현상이 많이 있기에 자연스러운 \(p\)진 기하 이론을 세우는 것이 쉽지 않지만, 정수론의 측면에서 \(p\)진 해석은 \(p\)의 거듭제곱에 대한 합동에 해석학의 이론과 직관을 적용하게 하는 유용한 통역기라는 측면도 살펴보았다. \(p\)진수라는 생소하고 특이한 수 체계가 정수론에 안착할 수 있었던 이유는 \(p\)진수를 사용하여 정수론에 중요한 결과를 얻어낼 수 있기 때문이다.
3편 “p진수를 활용한 슬기로운 방정식 풀이 上”과 4편 “p진수를 활용한 슬기로운 방정식 풀이 下”에서는 다변수 이차방정식의 유리수해의 존재성 판별에 \(p\)진수가 유용하게 쓰임을 설명하였다. 이는 20세기 초반 하세H.Hasse가 얻어낸 결과로, 역사적으로 \(p\)진수가 정수론에 중요한 개체로 자리 잡는 계기가 되었다.
5편 “p진 함수의 세계”에서는 \(p\)진 초월함수와 미분방정식을, 6편에 해당하는 이번 글에서는 \(p\)진 기하에 대해 다루었다. 두 연재글 모두 시작점은 실수·복소수 위에서 성립하는 해석과 기하의 특정 정리와 증명이, \(p\)진수 위에서도 비슷한 형태로 성립하는 현상이었다. (5편의 경우 미분방정식의 국소적 해의 존재성에 관한 코시의 정리, 6편의 경우 원환면의 점과 어떤 이변수 삼차 방정식의 해를 연결하는 바이어슈트라스의 정리와 테이트의 \(p\)진 버전이 시작점이다.)
\(p\)진 해석과 기하는 지난 세기부터 정수론의 중요한 도구로 응용되어 왔다. 특히 \(p\)진 기하는 최근 작고한 정수론의 대가 테이트가 남긴 중요한 수학적 유산 중 하나이며, 숄체가 2018년 필즈상을 수상하게 된 주요 연구업적이기도 하다. \(p\)진 기하나 숄체의 업적에 대한 소개 요청이 종종 있었고, 본 연재글 역시 부족하나마 이런 수요를 충족하기 위해 기획되었다.
막상 연재를 마무리하려고 하니 부족한 결과물이지 않았는가 하는 아쉬움이 짙게 남는다. 굳이 변명을 보태자면 (물론 수학의 다른 분야에도 해당하는 이야기지만) \(p\)진 기하이론 역시 상당히 추상적인 이론이고 정수론 역시 20세기 후반부터 추상화되어 왔기에, 비전문가에게 관련 내용을 설명하는 것에 어려움이 따르는 것도 사실이다. 어쨌든 비록 부족하지만 독자들이 조금이라도 흥미로운 측면을 찾을 수 있는 글이었기를 바라면서 연재를 마무리하고자 한다.