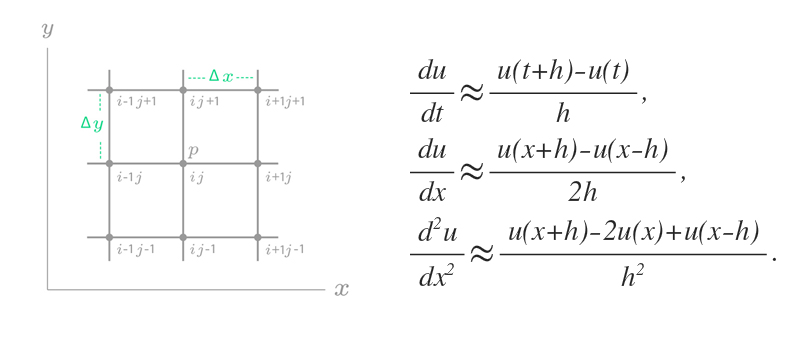계산수학이란 수학적 문제에 대하여 효율적이고 믿을 수 있는 컴퓨터 해를 구하고자 하는 연구 분야이다. 계산수학은 컴퓨터가 생겨나기 이전인 16세기경부터 발달하였는데 네이피어의 로그의 발견, 뉴턴의 비선형방정식 해법과 보간법 등이 그 예다. 20세기 들어서 컴퓨터가 생겨나고 선형방정식계와 상미분방정식, 편미분방정식 등을 푸는 방법들이 폭발적으로 개발되었다. 또한 병렬계산기가 만들어 지면서 이를 활용하는 수치방법들이 개발되고 있다. 이 글에서는 계산수학의 태동과 발전을 살펴보고 앞으로 어떻게 발전해 나아가게 될지를 살펴본다.
계산수학이란?
계산수학은 엄밀한 수학적 이론을 이용하여 오차를 분석하고, 대용량 계산과 병렬 계산 알고리즘을 만들어내며, 계산 모델링과 이 모델에 대한 모의실험을 하는 분야이다. 즉 계산수학이란 계산을 보다 정확하게, 보다 편하게 하기 위한 수학이라고 할 수 있다.
수학의 역사는 사실 계산의 역사라고 할 수 있다. 기존의 방법으로는 계산의 오차가 많이 생겼고, 특히나 천문학이 발달하기 시작하면서 큰 계산을 정확하게 하기 위한 필요성 때문에 컴퓨터가 생겨나기 이전 16세기경부터 계산수학은 계산을 편하게 하기 위해 비약적으로 발달하기 시작하였다. 먼저 계산수학이 어떻게 발전하게 되었는지 그 역사와 과정을 살펴보도록 하자.
계산수학의 역사와 발전 과정
• 로그의 발견
기원전 바벨로니아인들은 두 자연수의 곱셈을 제곱 계산과 덧셈과 뺄셈을 이용하여 계산하는 방법을 개발하였는데, 다음의 식으로 계산하였다. \[\left[ \frac { (x+y)^{ 2 } }{ 4 } \right] -\left[ \frac { (x-y)^{ 2 } }{ 4 } \right] =xy.\]
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \( { n }^{ 2 }/4\) | 0 | 0 | 1 | 2 | 4 | 6 | 9 | 12 | 16 | 20 | 25 | 30 | 36 | 42 | 49 | 56 | 72 |
로그의 발견은 먼저 네이피어1550-1617에 의해 다음과 같은 운동방정식으로부터 출발하였다.보통 로그는 자리수를 줄여서 계산을 편하게 하기 위해 생겨났다고 생각할 수 있지만 곱셈을 쉬운 덧셈으로 바꾸어서 계산하는 방법으로 개발되었다고도 할 수 있다. 17세기가 되면서 천문학자들이 기하적 변화에 따른 산술적 변화를 보게 되면서 로그가 발견되었다. 17세기에 수학의 최고의 발견이라고도 여겨지는 로그는 존 네이피어 John Napier, 1614와 요스트 뷔르기Joost Bürgi, 1620에 의해 독립적으로 발견된다.
점 \(d\)가 \(T\)에서 \(S\)로 점점 속도를 줄여가면서 이동하고, 동시에 점 \(c\)가 \(b\)에서 오른쪽으로 같은 속도로 움직이는 것을 미분방정식으로 나타내면 다음과 같다. \begin{align*}\dfrac{d}{dt}(r-x) &= x,\quad x(0)=r\\\dfrac{d}{dt}y &= r, \quad y(0)=0.\end{align*} 위의 미분방정식을 \(x\)와 \(y\)에 관해서 풀면, \(x = re^{-\frac{y}{r}}\)가 되는데, 네이피어는 \(r=10^7\)으로 잡고, \[y := \operatorname{Nap.Log}x = 10^7\operatorname{ln}\dfrac{10^7}{x}\]를 네이피어 로그라고 정의하였다. 네이피어가 살던 시대에는 반지름이 \(r=10^{7}\)인 원에서 \(\sin\)함수를 생각하였기 때문에, \(\operatorname{Sin}x = 10^7 \sin x\)를 \(x\)대신 사용하면, 현대개념으로 네이피어 로그를 다음과 같이 이해할 수 있다. \[\operatorname{Nap.Log}\operatorname{Sin}x = -10^{7}\ln\sin x.\] 여기서 \(N = \operatorname{Sin}x = 10^{7}(1-10^{-7})^{L}\)이라 하면, \[L = \log_{1-10^{-7}}\dfrac{N}{10^{7}}= \dfrac{\ln (N/10^7)}{\ln (1-10^{-7})}\approx \dfrac{\ln N/10^{7}}{-10^{-7}} = 10^{7}\ln\dfrac{10^{7}}{N},\] 즉, \(L \approx \operatorname{Nap.Log} N\)이 된다. 네이피어는 20년간 5에서 천만 사이의 자연수 \(N\)에 대해 위의 등식을 만족시키는 \(L\)값을 모두 찾아내었다. 하지만 다음의 식\[\operatorname{Nap.Log} xy = \operatorname{Nap.Log}x + \operatorname{Nap.Log}y – \operatorname{Nap.Log}1\]에서 마지막 \(0\)이 아닌 항(\(\operatorname{Nap.Log}1\)) 때문에 네이피어 로그로는 곱셈을 덧셈으로 바꿔서 계산할 수가 없었다. 그래서 브릭스Henry Briggs, 1561-1630가 1617년 반지름이 \(10^{10}\)인 원을 사용하여 새로운 로그를 정의하는데, 현대개념으로\[\operatorname{Bri.Log}x = 10^{9}\log_{10}x\]가 된다. 즉, 브릭스는 상용로그를 발견하였다. 그리고 브릭스는 1617년에 1에서 1000까지의 14자리 상용로그 표를 만들었다. 로그의 발견은 인류 최초로 계산을 편하게 하기 위한 획기적인 아이디어라고 볼 수 있을 것이고, 계산수학의 출발점이라고 할 수 있다.
• 뉴턴-랩슨 방법
1600년대에는 방정식을 푸는 방법에 관심이 많았다. 이 때 뉴턴은 1669년 \(y^3-2y-5=0\)의 해를 구하는 방법으로 다음과 같이 생각하였다. 해 하나의 정수부가 \(2\)이므로, 다음의 과정을 반복적으로 계산하였다.
· \(y=2+p\)로 치환하면 \(p^{3}+6p^{2}+10p-1=0\)이므로, \(p\)는 대략 \(0.1\),
· 다시 \(p=0.1+q\)로 치환하면 \(q^{3}+6.3q^{2}+11.23q+0.0061=0\) 이어서 \(q\)는 대략 \(-0.0054\),
· 다시 \(q=-0.0054+r\)로 치환하여 같은 방식으로 변형하여 식을 풀면 \(r\)은 대략 \(0.00004853\),
· 이러한 과정을 반복하면 \(y\)는 대략 \(2.09464853\)이다.
방정식을 바로 풀기는 힘들지만, 위의 과정을 보면 비교적 쉬운 계산을 반복적으로 수행함으로써 해를 얻을 수 있는데, 사실 위의 반복과정에서 \(p\), \(q\)는 다음 계산에서 분수값들과 같다. \(f(x) = x^{3}-2x-5\)라고 하였을 때,
· \(x_0=2\)에서 \(-\dfrac{f(x_0)}{f'(x_0)}=0.1\),
· \(x_1=2.1\)에서 \(-\dfrac{f(x_1)}{f'(x_1)}=-0.0054\).
1690년 랩슨Joseph Raphson이 위의 과정을 체계적으로 정리해서 발표하였는데, \(f(x)=0\)의 해는 초기 추측 \(x_0\)로부터, 다음의 식\[x_{n+1} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \qquad n=0,1,2,3,\ldots\]을 반복적으로 시행하여 얻을 수 있다는 것이다.
하지만, 랩슨이 발표한 위의 방법을 뉴턴은 이미 알고있었다고 여겨진다. 그 이유는 뉴턴이 1675년에 발표한 \(A\)의 제곱근과 삼승근, 사승근을 적당한 추측 \(B\)로부터 구하는 공식\[A^{1/n} = \frac{(n-1)B + A/B^{n-1}}{n}, \qquad (n = 2,3,4)\]에서 방정식 \(f(x) = x^{n}-A = 0\)에 랩슨의 방법을 적용하면\[x_{i+1} = x_{i} – \frac{x_{i}^{n}-A}{nx_{i}^{n-1}} = \frac{(n-1)x_{i} + A/x^{n-1}}{n}\]을 얻을 수 있기 때문이다.
• 최소자승법
이후 1805년 르장드르Adrien-Marie Legendre가 최소자승법을 발표하였는데, 미지수 \(n\)개를 가지는 \(m\)개의 (\(m > n\)) 방정식\[\sum_{j=1}^n a_{ij} x_j \approx r_i \qquad (i=1,2, \ldots,m)\]에서 각 \(i(i=1,2,\ldots,n)\)에서 관측된 자료 \(r_{i}\)와의 차이인 오차\[e_{i} = \sum_{j=1}^n a_{ij}x_{j} – r_{i}\]의 제곱의 합 \(\sum_{i=1}^n e_{i}^{2} \)을 가능한 작게 만드는 \((x_{1}, x_{2}, \ldots , x_{n})\)을 다음과 같이 구하는 방법이다.\[A^{T}A \left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right] = A^{T}\left[\begin{array}{c} r_{1} \\ r_{2} \\ \vdots \\ r_{n} \end{array} \right], \quad A = \left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right].\] 하지만 가우스는 1809년에 자신은 이미 1795년부터 이 방법을 사용하였다고 언급하였다.
• 가우스의 수치적분
가우스의 수치적분법은 뉴턴과 라이프니츠 시대를 지나 미적분이 성행하던 시절인 1814년에 발표되었다. 기존의 뉴턴-코츠 방법은 구간 \(a\)에서 \(b\)까지 \(y=f(x)\)를 적분할 때, \((n+1)\)개의 점 \(x_{k} = a+ k\frac{b-a}{n}\) (단, \(k=0,1,2,\ldots,n)\)에서의 함수값을 구한 후, 각 점에서 적당히 가중치 \(w_{k}\) \((k=0,1,2,\ldots,n)\)을 주어서 평균값을 구하여 다음과 같이 적분을 근사시키는 것이다.\[\int_a^b f(x)\,dx \sim w_0f(x_{0}) + w_{1}f(x_{1}) + \cdots + w_{n}f(x_{n}).\] 뉴턴-코츠 방법은 위의 적분근사를 \(f\)가 \(n\)차 다항식인 경우에는 정확한 값을 주는 적분 공식이 되도록 \(w_{k}\)값들을 구하였다. 하지만 가우스의 생각은 \(w_{k}\)값뿐만 아니라, \(x_{k}\)도 잘 조정할 수 있는 파라메터로 보면 \((2n+2)\)개의 파라메터를 가지고 \((2n+1)\)차 다항식까지 정확히 계산되게 만들 수 있다는 것이다. 가우스의 이 수치적분을 가우스 구적법Gaussian Quadrature이라고 한다. 적분 구간을 \([0, 1]\)이라 하면, 실제로 \(x_{k} \hspace{1mm} (k=0,1,2,\ldots,n)\)들은 구간 \([0,1]\) 에서 \((n+1)\)차 르장드르 다항식의 해가 된다.
• 반올림 오차
또 다른 가우스의 큰 업적 중 하나는, 반올림 오차에 대해서 처음으로 고민했다는 것이다. 우리가 실제 수학 계산을 할 때, 예를 들어, 로그나 삼각함수 계산에 있어서 유한자리만 택하고 반올림하기 때문에 필연적으로 오차가 발생할 수밖에 없다. 그래서 계산을 여러 번 수행하다보면 오차가 누적이 되어 그 결과가 틀릴 수도 있다는 것을 가우스가 생각한 것이다. 가우스는 이러한 현상에 대해서 체계적인 접근을 처음으로 시도하였고 현대개념의 알고리듬의 안정성stability, 즉 이런 오차들이 누적이 되어도 그 결과를 믿을 수 있는 알고리듬인지 아닌지에 관한 고찰이 가우스로 부터 시작되었다.
• 선형방정식의 해법
앞서 언급한 르장드르 최소자승법은 결국 행렬방정식 \(Ax=b\)를 풀어야하는 문제가 생겨난다. 앞서 뉴턴의 접근과 비슷한 방법으로 야코비C. G. J. Jacobi는 행렬방정식에서 행렬의 주대각선 항에 있는 값이 다른 항보다 클 때 나머지 대각선에 없는 항은 무시하는, 즉, \(Ax=(D+L+U)x = b\)에서 \(L\)과 \(U\)를 무시하고, 대각선 부분인 \(D\)에 관해서 방정식을 반복적으로 풀어나가는 다음의 방법을 제시한다.
· 첫 번째 근사: \(Dy=b\)에서 \(x=y+\Delta\)로 치환하면 \(D\Delta + (L+U)(y+\Delta) = 0\),
· 두 번째 근사: \(D \Delta = -(L+U)y \)에서 \(x=y+\Delta + \Delta^{1} \)으로 치환하면 \(D\Delta^{1} + (L+U)(\Delta + \Delta^{1}) = 0\),
· 세 번째 근사: \(D \Delta^{1} = -(L+U)\Delta\)에서 ….
· 이 과정을 반복하면 \(x = y + \Delta + \Delta^{1} + \Delta^{2} + \cdots \)을 얻는다.
위의 반복 과정은 현대적인 개념에서 대각 계수가 다른 계수보다 클 때 다음의 야코비 방법으로 다시 쓸 수 있다.\[Dx^{(n+1)} = b – (L+U)x^{(n)}, \quad x^{(0)} = 0.\] 그러면, \[x^{(n)} = y + \Delta + \Delta^{1}+ \cdots + \Delta^{n-2}\]이 된다.
• 초기치 상미분방정식의 수치해법
코시는 초기치 상미분방정식\[\frac{\partial y}{\partial x} = f(x,y), \qquad y(x_{0}) = y_{0}\]에서 해의 존재성을 증명하였는데, \(f\)와 \(\frac{\partial f}{\partial y}\)가 영역 \(\lvert x-x_{0}\rvert \leq a\), \(\lvert y-y_{0}\rvert \leq b\)에서 연속이고, \(x_{i} = x_{0} + ih\)라 할 때, 수열 \(y_{i+1} = y_{i} + hf(x_{i}, y_{i})\), (\(i=0,1,\ldots,n-1\))은 적당한 조건 하에서 \(h \rightarrow 0\)일 때, 위의 미분방정식의 해로 수렴한다는 것이다. 여기서 해의 존재 증명을 위해 사용한 방법을 오일러는 초기치 상미분방정식의 수치적인 해법으로 사용하게 된다. 오일러의 방법은 미분연산을 1차식으로 근사시켰기 때문에, 수렴속도의 차수는 1차가 된다. 뒤이어 룽게C. D. T. Runge, 1895와 훈Karl Heun, 1900, 쿠타Martin W. Kutta, 1901는 각각 2, 3, 4차의 방법들을 개발하게 된다. 참고로, 훈의 방법은 다음과 같다.\[\begin{cases} k_{1} = hf(y_{n}), \qquad k_{2} = hf(y_{n} + \frac{1}{3}k_{1}), \qquad k_{3} = hf(y_{n} + \frac{2}{3}k_{2}), \\
y_{n+1} = y_{n} + \dfrac{1}{4}k_{1} + \dfrac{3}{4}k_{3}. \end{cases}\] 하지만 계속해서 차수를 높여가는 방법들이 나오지 않는 이유는 차수를 높여가면 한 번 계산할 때의 계산량이 늘어나기 때문에 계산횟수가 줄어들어, 수렴은 빠르지만 어떤 특정 차수 이상 올라가면 이익이 되지 않기 때문이다.
• 유한차분법
편미분방정식을 다루는 가장 쉬운 수치해법은 유한차분법Finite Difference Method이다. 유한차분법은 영역에서 격자를 만든 다음 미분의 개념을 다음과 같이 유한 차분 공식으로 바꿔서 해를 구하는 것이다.
유한차분법은 실제 프로그래밍으로 구현하기에 비교적 쉽고 계산과정이 복잡하지 않다는 장점이 있는 반면에 영역의 형태가 복잡한 모양, 즉 직사각형 모양과 같이 단순하지 않은 영역에서는 적용하기 힘들고 물리적인 보존의 개념이 필요한 문제에 적용하기에는 어려운 단점이 있다.
• 리처드슨 방법
1910년 리처드슨Lewis F. Richardson은 푸아송 방정식 (\(\nabla^{2}\varphi = 0\)), Helmholtz 방정식 (\((\nabla^{2} + k^{2})\varphi = 0\)), biharmonic 방정식 (\(\nabla^{4}\varphi = 0\)), biharmonic 방정식의 고유치 문제 (\((\nabla^{4} – k^{4})\varphi = 0\))들의 유한 차분법을 제시하였다. 유한차분법을 사용하면 각 격자에서의 미지수 값들을 풀어야하기 때문에 행렬방정식 \(Ax=b\)가 나오게 되는데, 1925년 리처드슨은\[Ax=b, \quad A = \begin{pmatrix} -4 & 1 & 0 & 1 \\ 1 & -4 & 1 & 0\\ 0 & 1 & -4 & 1 \\ 1 & 0 & 1 & -4 \end{pmatrix},\quad b = \begin{pmatrix}-3 \\ -7 \\ 0 \\ 0 \end{pmatrix}\]을 반복적으로 푸는 수치적 방법(리처드슨 방법)을 다음과 같이 제시하였다.\[x^{(r+1)} = x^{( r )} + a_{r}^{-1}(Ax^{( r )} – b), \qquad a_{r} > \frac{1}{2}|\lambda_{\max}|.\] 리처드슨은 시간 종속 열방정식 \[\frac{\partial \phi}{\partial t} = \frac{\partial^{2} \phi}{\partial x^{2}}\]도 유한차분법을 사용하여 \[\phi_{r,s+1} = \phi_{r,s-1} + 2\dfrac{\Delta t}{(\Delta x)^2} (\phi_{r+1,s} – 2\phi_{r,s} + \phi_{r-1,s})\]와 같이 풀 수 있다고 하였지만 컴퓨터가 없었기 때문에 상당한 수준까지 이 방법으로 계산을 하지 못하여서 수치적인 알고리즘의 안정성에 관해서는 알지 못하였다. 그 후에 시간 종속 열방정식에 대한 리처드슨 방법이 안정적이지 않다는 것이 밝혀지게 된다.
• 완화법
당시에는 어떻게 수치적으로 행렬방정식 \(Ax=b\)를 잘 풀 것인가에 관한 이슈들이 계속 문제로 남아있었다. 그 후 1935년에 사우스웰Richard V. Southwell이 완화법을 소개하게 되는데, 사우스웰은 \(Ax=b\)를 다음과 같이 생각하였다.
· \(x\): 변위 벡터
· \(b\): 프레임의 결합 부위에서의 힘
· 남은 힘 (residual force): \(r^{(n)}=Ax^{(n)}-b\)
즉, 현재의 남은 힘이 큰 결합 부위를 골라서 남은 힘을 줄여나가도록 변위를 변형하여 힘을 줄여나가는 것이 사우스웰이 제안한 방법이다.
오른쪽의 예시는 1차원 푸아송 방정식을 유한차분법으로 이산화시키고, 양쪽 끝점에서 \(f_{0}\), \(f_{5}\)와 중간에서의 힘 \(b_{1}, b_{2}, b_{3}, b_{4}\)값들이 주어졌을 때, 초기값 \(f_{1}=f_{2}=f_{3}=f_{4}=0\)로 부터 완화법을 통해 \(f_{1},f_{2},f_{3},f_{4}\)를 찾아나가는 과정을 보여주고 있다. 먼저, 네 번째 결합 부위에서 남은 힘이 가장 크므로 선형적으로 변위들이 증가하도록 네 번째 변위를 \(-1280\)으로 변형시켜 남은 힘을 \(0\)으로 만든다. 그 다음, 두 번째 결합 부위에서 변위를 \(-40\)으로 바꾸면 2,3,4번째 남은 힘은 모두 \(0\)이 되고, 남은 첫 번째 남은 힘도 \(0\)으로 만들기 위해 선형적으로 변위들을 각각 \(32,24,16,8\)로 변형시킨다. 그러면 각 결합 부위에서 남은 힘이 모두 \(0\)이 되고, 변형된 변위들을 모두 합쳐서 해 \(f_{1}, f_{2}, f_{3}, f_{4}\)을 찾게 된다.
현대적인 완화법으로는 야코비, 가우스-자이델, SORSuccessive Over Relaxation 방법들이 있는데, 세 방법 모두 초기 추측 \(x^{(0)}\)로부터 전체적으로 한꺼번에 남은 힘을 줄여나간다.
• 켤레기울기법
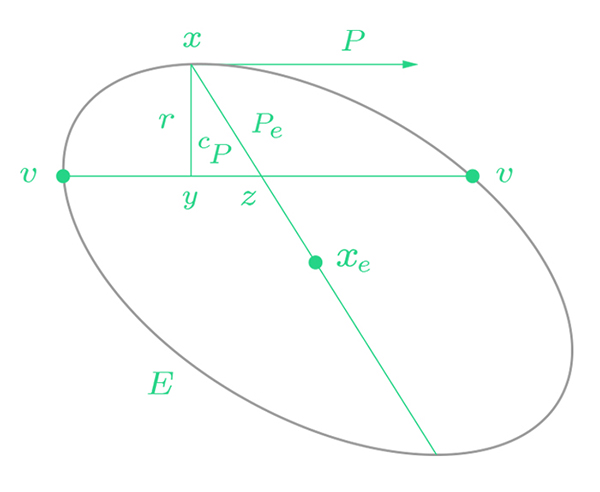
앞서 소개한 완화법과는 다른 시각으로 1952년 스티펠Eduard Stiefel과 헤스테네스Magnus Hestenes, 란초스Cornelius Lanczos가 켤레기울기법Conjugate Gradient 방법을 제시하였다. 이 방법의 아이디어는 \(Ax=b\)의 해를 찾는 것은, \(A\)가 symmetric positive definite라는 가정 하에서, \(f(x) = \frac{1}{2}x^{*}Ax – b^{*}x\) 의 minimizer(stationary point)를 찾는 것과 동일하다는 사실에서 출발한다. 다시 말해, 이차식의 최소화 문제는 접선의 기울기가 \(0\)이 되는, 즉, 미분하여 “일차식\(0\)”의 문제와 같다는 것이다. 켤레기울기법은 그림과 같이 residual 벡터 \(r\)과 \(f(x) = \frac{1}{2}x^{*}Ax – b^{*}x\)의 등고선에 접하는 벡터 \(p\)가 수직이라는 것으로부터 \(p\)와 \(x_{e}-x\)가 \(A\)-orthogonal, 즉, 켤레conjugate라는 개념을 도입한다.
\begin{align*}r&=-\nabla f\left( x \right) =b-Ax=A({ x }_{ e }-x), & p&\bot r,\\ { p }_{ e }&=r+bp,&b&=-\frac { { p }^{ * }Ar }{ { p }^{ * }Ap } ,\\ { x }_{ e}&= x+a{ p }_{ e }, &a&=-\frac { { p }_{ e }^{ * }Ar }{ { p }_{ e }^{ * }A{ p }_{ e }^{ * } } .\end{align*}
위의 그림과 같은 2차원 최소화 문제는 1차원 선 위의 켤레 방향을 따라서 내려가면 해를 찾을 수 있게 되고, 켤레기울기법은 이를 일반화화여 \(\mathbb{R}^{n}\)상의 최소화 문제를 \((n-1)\)차원의 초평면에서 해를 찾는 문제로 차원을 줄여나가는 다음의 과정을 반복적으로 수행하여 해를 찾는다.
· \(x_{1}\)에서 시작.
· \(p_{1}\)을 적당히 잡음.
· \(x_{2} = x_{1} + a_{1}r_{1}\)로 \(f(x_{2})\)를 최소화 시키는 \({1}\)을 선택.
· \(p_{1}\)에 켤레인 공간에서 \(x_{3}\)을 잡음, (\(x_{3} = x_{2}+b_{1}p_{1}\)).
· \(x_{3}\)에서 시작하여 위의 과정을 반복.
켤레기울기법은 차원을 하나씩 줄여나가면서 해를 찾아나가므로, 행렬 \(A\)의 size \(n\)번 만에 수렴하는 것이 보장되기 때문에 기존의 경사 하강법Gradient Descent Method의 속도 문제를 해결할 수 있다는 점에서 의미가 있다.
현대의 계산수학
• 컴퓨터의 등장
이처럼 많은 사람들의 계산에 대한 수학적 발견과 업적 후에 컴퓨터가 등장하였지만, 이미 1600년대부터 기계식 계산 장치에 대한 발전이 있었다. 1642년에 덧셈과 뺄셈만 가능했던 파스칼의 수동계산기가 있었고, 1671년 라이프니츠가 이를 개량하여 곱셈과 나눗셈이 가능하게 하였다. 그 후 1936년 튜링Alan Turing은 긴 테이프에 쓰여 있는 여러 가지 기호들을 일정한 규칙에 따라 바꾸는 기계의 개념을 제시하여 알고리듬을 수행하는 컴퓨터의 기초적인 이론을 제공하였다. 제2차 세계대전 중에 독일과 영국, 미국에서 연산장치를 가진 초기 형태의 컴퓨터가 고안되었고, 현대적인 컴퓨터로는 1946년 18,000여개의 진공관을 사용한 무게 30톤의 에니악ENIAC과 1952년 폰 노이만의 프로그램 내장방식의 에드박EDVAC이 만들어진다. 이처럼 컴퓨터가 등장하면서 계산 능력이 늘어남에 따라 코딩이 쉬운 알고리듬을 선호하게 되고 오랜 시간 반복되는 계산이 가능해지게 되었다.
• 유한요소법
컴퓨터의 등장과 함께 좀 더 다양한 문제를 풀고자하는 수요가 생겨나면서 유한요소법Finite Element Method이 제시된다. 유한요소법이란 영역의 기하학적 모양의 제약에서 벗어나, 주어진 영역을 삼각화해서 그 삼각형 영역들 위에 있는 함수로 근사화하는 수치해법이다.
예를 들어, 다음과 같은 푸아송 방정식 \[\begin{cases} -\nabla^{2}u = f & \text{in} & \Omega \\
u = 0 & \text{on} & \partial\Omega \end{cases}\]에서 먼저, 다음의 적분식을 만족하는 함수 \(u\)를 찾고 (변분 문제) \[\int_\Omega \left(\dfrac{\partial u}{\partial x}\dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}\dfrac{\partial v}{\partial y}\right) dx = \int_\Omega fv dx, \quad \forall v \in V,\] 그 다음, \(u\)를 기저함수basis function들의 선형 결합으로 표현한다. (갤러킨Galerkin 방법)
즉, 유한요소법이란 원래 연속함수였던 \(u\)를 유한 차원의 기저함수들의 선형 결합으로 근사시키는 것이다. 따라서 node에서의 함수값만 찾으면 되므로, 유한 차원의 문제로 바뀌게 된다.
대부분의 수학자들은 유한요소법을 함수를 다항식 여러 조각으로 근사하는 것으로 본다. 또는 삼각형 mesh위에서 변분 문제variational problem의 근사로 보는 관점도 있고, subdomain 위에서의 국소적 근사들의 수열로부터 mesh를 잘게 쪼개면서 원래 미분방정식의 해로 근사를 얻는 것이라고 보는 관점도 있다. 그리고 유한요소법은 영역을 작은 영역으로 분할하고 유한 요소를 결합하여 외력과 경계조건을 부가하고 국소적 다항식의 근사를 하는 것이라고 보는 시각도 있다. 유한요소법은 이후 1950~1980년에 걸쳐 다양한 방법으로 공학 측면에서 개발되고, 이를 수학적으로 지원하게 된다.
• 병렬 컴퓨터의 등장과 영역분할법
1975년 세계 최초의 병렬 컴퓨터인 256개의 프로세서를 가진 ILLIAC IV와 1982년 4개의 병렬 벡터 프로세서를 가진 Cray X-MP가 등장하게 되면서 병렬계산을 하기 위한 방법들이 소개되는데, 그 중 하나로 영역분할법Domain Decomposition Method이 있다. 영역분할법의 장점은 병렬화가 쉽고, 복잡한 영역에서 문제를 단순한 영역의 문제로 바꿔주며, 영역별로 다른 수치기법을 적용할 수 있다는 것이다.
• 미래의 계산수학
지금까지는 하드웨어의 개발 속도에 맞춰서 알고리즘의 발전 속도 역시 증가해왔지만, 앞으로는 둘 다 발전 속도가 점차 느려지고 계속해서 발전하기 힘들어 질 것이다. 그래서 이제는 연소와 기상, 재료와 같은 현실 문제를 풀기위한 다양한 시도들이 많이 나오고 있지만 이러한 문제들이 점차 매우 큰 규모의 문제로 진화하고 있기 때문에 아직도 많은 과학과 공학문제를 풀기에는 컴퓨팅 파워가 부족한 것이 사실이다. 따라서, 이 같은 문제들을 해결하는 것이 계산수학이 앞으로 해결해야할 과제와 나아갈 방향이 될 것이다.
KAIST 수리과학과 이창옥 교수의 2015년 10월 2일 “정오의 수학 산책” 강연 내용을 발췌, 정리하였습니다.