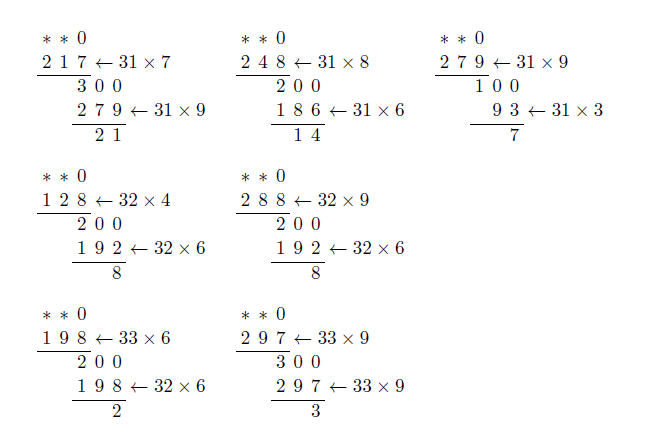[6월의 퍼즐 해설] 궁극의 진리를 향한 끝없는 탐구

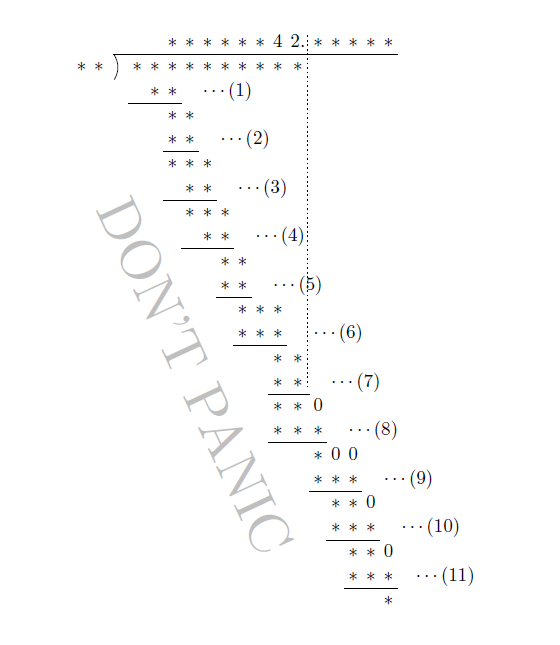
편의상 나누는 두 자리 수를 \(a\)라 하고 각 단계에 번호를 붙이자. 나눗셈 단계에서 위에서 내려오는 수가 명백히 0인 곳은 미리 표시하여 두었다.

(6)에서 \(a\)에 4를 곱한 결과가 세 자리 수이므로, \(25 \le a \le 99\)임을 알 수 있다. 또 (7)에서 \(a\)에 2를 곱한 결과가 두 자리 수이고 계산 결과도 두 자리 수이므로 \(2a\)가 90, 91, \(\dotsc\)가 될 수는 없다. 따라서 \(10 \le a \le 44\)가 된다. 그러면 \(25 \le a \le 44\)이다.

한편 (1)에서 세 자리 수에 두 자리 수를 뺀 결과가 한 자리 수이므로, \(a\)에 어떤 수를 곱하여 91과 99 사이의 수를 만들 수 있어야 한다. \(25 \le a \le 44\) 범위에서 이런 일이 가능한 \(a\)는 31, 32, 33의 세 가지이다.

(8)에서 일의 자리가 0인 세 자리 수에서 세 자리 수를 뺀 결과가 한 자리 수인데, (9) 단계에서 0을 두 번 썼다는 것은 (8) 단계의 계산 결과가 4보다 작다는 뜻이다. 만약 (8) 단계의 계산 결과가 4였다면 (9) 단계에서는 \(40-31\), \(40-32\), \(40-33\)과 같은 계산을 할 수 있기 때문에 (9) 단계의 \(\ast00\)이 나올 수 없다.

그러면 다음과 같은 경우들을 생각할 수 있다.

이 가운데 (9) 단계와 같이 계산 결과가 두 자리 수가 되는 것은 처음 두 경우뿐이다. 따라서 \(a=31\)임을 알 수 있다. 이어서 처음 두 경우를 계속 계산해 보면, (11) 단계에서 계산한 결과가 한 자리 수가 되는 것은 두 번째 경우밖에 없음을 알 수 있다. 지금까지 알아낸 결과를 표시하면 다음과 같다.


이제 (8) 단계의 계산 결과가 한 자리 수 3이 되려면 \(250-248=2\)가 될 수밖에 없다. 그러면 (7) 단계의 계산 결과가 두 자리 수 25가 되어야 하므로, 여기는 \(87-62=25\)가 된다. 이런 식으로 차례대로 윗 단계로 올라가며 채워보면 다음과 같다.

(4) 단계는 세 자리 수에 두 자리 수를 빼서 한 자리 수가 나와야 하므로, 빼는 두 자리 수가 적어도 91은 되어야 한다. 31의 배수이면서 91보다 크거나 같은 수는 93이므로, (5) 단계의 빼어지는 두 자리 수는 첫 번째 자리의 수가 7, 8, 9 가운데 하나라야 한다. 그리고 여기에 다시 31의 배수를 뺀 결과가 1이 되어야 하므로, 이런 일은 \(94-93=1\)일 때만 가능하다. 따라서 (4) 단계는 \(102-93=9\)임을 알 수 있다.

(3)에서 세 자리 수에 두 자리 수를 뺀 결과가 10이 되므로 이 단계는 \(103-93=10\)이 되고, (1) 단계의 계산 결과로부터 (2)에서 빼어지는 수의 첫 번째 자리가 7, 8, 9 가운데 하나이므로 (2) 단계는 \(72-62=10\)이 될 수밖에 없다.

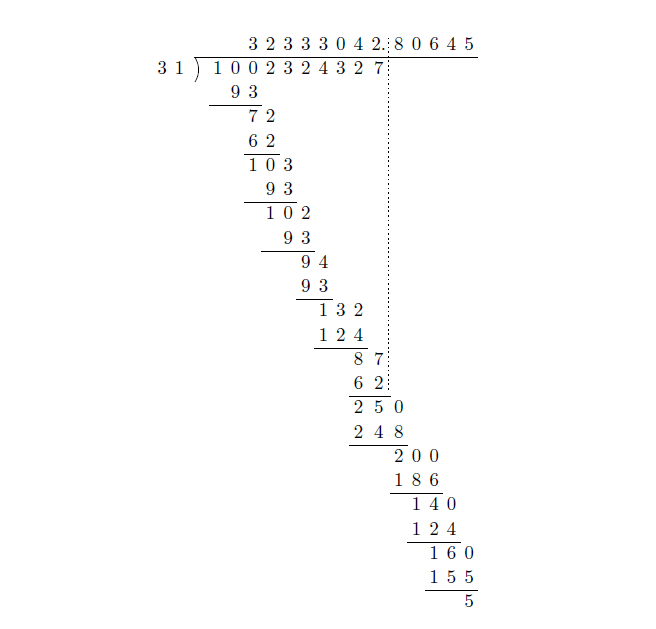
이상의 결과로 남은 자리를 모두 채우면 다음과 같은 계산 과정을 완성할 수 있다.

제수를 x라고 하자. x는 두 자리 자연수이다.

다음으로 밝혀져 있는 두 숫자, 즉 몫의 십의 자리 4와 일의 자리 2에 해당하는 나눗셈 연산을 보면 보면 4x 는 세 자리 수, 즉 100 이상이고, 2x는 두 자리 수, 즉100 미만임을 알 수 있다.
따라서 x는 25 이상 50 미만의 두 자리 수이다.

다음으로 피제수의 맨 앞 세 자리와 몫의 맨 앞자리만 끊어서 보면, 세 자리 수(a)에서 x의 배수인 두 자리 수(b)를 뺀 값이 한 자리 수임을 알 수 있다. a가 세 자리 수라는 것은 100 이상이라는 의미이고, b가 두 자리 수라는 것은 99 이하라는 의미이다. 그리고 a와 b의 차가 한 자리 수임을 이용하여 양쪽의 범위를 구하면 a는 100 이상 108 이하, b는 91 이상 99 이하이다. 따라서 a의 백의 자리는 1, 십의 자리는 0, b의 십의 자리는 9이다.

다시 x로 돌아간다. 25 이상 49 이하의 수 중 정수배를 했을 때 91~99 사이의 수가 나올 수 있는 수는 31, 32, 33, 46, 47, 48의 6개이다.

일단 여기까지 좁혀 놓고 몫의 일의 자리 ‘2’를 보자. 두 자리 수(c)에서 2x인 두 자리 수(d)를 뺀 차가 두 자리 수이다. 즉 c-d는 10 이상이다. 두 자리 수인 c는 99 이하이므로 d는 89 이하여야 하고, 그 반인 x는 44.5 이하(자연수이므로 44 이하)가 된다. 그렇다면 x 후보에서 46, 47, 48이 제외되고, x의 첫 자리는 3으로 확정된다(x는 31, 32, 33 중 하나). 여기서 a와 b로 돌아가 보면, b는 91 이상이므로 몫의 맨 앞자리는 3으로 확정된다(즉 b=3x이다). 그리고 아래의 개별 뺄셈 연산 중 ‘세 자리 수에서 두 자리 수를 빼는 연산’이 나오는 부분은 몫의 해당 자리의 수가 3으로 확정되고, 세 자리 수의 백의 자리는 1로 확정된다.

여기까지 좁혀놓고 난 다음에는 몫의 소수점 아래 부분을 주목해 보자. 문제를 보면 피제수는 자연수이므로 소수점 아래 부분은 모두 0이다. 그런데 소수점 아래 첫째 자리의 연산은 세 자리 수 – 세 자리 수이고, 그 차(e)는 한 자리 수이며 e에 아래 두 자리를 붙여 다음 뺄셈 연산을 하는 것(즉, 몫의 소수점 아래 둘째 자리는 0이다)을 알 수 있다. 따라서 다음 줄의 세 자리 수는 100e인데, 9x의 최대치가 297이라는 점을 고려하면 100e가 400 이상이 될 수는 없다(이 경우 0을 하나만 붙이고 소수점 아래 둘째 자리 연산을 해야 한다). 결국 e는 1, 2, 3 중 하나이다. 다음으로 소수점 아래 셋째 자리 연산을 보면 100e에서 100e보다 작은 x의 배수 중 가장 큰 수(f)를 뺀다는 점에 주목을 해 보자. x가 31에서 33 사이이므로 f는 124, 128, 132, 155, 160, 165, 186, 192, 198, 217, 224, 231, 248, 256, 264, 279, 288, 297 중 하나이다. 그런데 나눗셈의 정의상 100e-f는 x보다 작은 수여야 하고, 두 자리 수라는 점은 명시되어 있으므로 e와 f의 조합으로 가능한 것은 (2, 186), (3, 279), (3, 288)밖에 남지 않는다.

세 쌍을 갖고 다음 줄(소수점 아래 넷째 자리)로 내려가보자. 다음 줄의 마지막 자리는 0이므로 세 자리 수(g)는 10*(100e-f)가 되고, 여기에서 g보다 작은 x의 배수 중 가장 큰 수(h)를 빼면 두 자리 수가 나와야 한다. 여기부터는 반복작업을 한다.
1) 2, 186 : x=31, g=140, h=124, 차는 16
2) 3, 279 : x=31, g=210, h=186, 차는 24
3) 3, 288 : x=32, g=120, h=96, 차는 24

다음은 소수점 아래 다섯째 자리, 마지막 연산이다. 역시 마지막 자리는 0이므로 세 자리 수 i는 10*(g-h)가 되고, 여기에서 i보다 작은 x의 배수 중 가장 큰 수 j를 빼면 한 자리 수가 나와야 한다.
1) 2, 186 : x=31, i=160, j=155, 차는 5
2) 3, 279 : x=31, i=240, j=217, 차는 23(조건 불충족)
3) 3, 288 : x=32, i=240, j=224, 차는 16(조건 불충족)

이 시점에서 e=2, f=186, x=31(f=6x)임을 특정할 수 있다. 이것을 바탕으로 아래부터 역으로 채워나가면 피제수의 백의 자리까지는 쉽게 채울 수 있다. 천의 자리에서는 경우가 갈리는데, 연산은 두 자리 수(k) – x의 배수인 두 자리 수(l)이고 차는 딱 1이다. 그렇다면 가능한 k와 l의 조합은 (32, 31), (63, 62), (94, 93)의 셋이다. 그런데 만의 자리 연산이 백의 자리의 수가 1인 세 자리 수(m) – 십의 자리의 수가 9이고 x의 배수인 두 자리 수(n)이고 차는 한 자리 수라는 점을 보면, n=3x=93으로 확정되므로 m은 100 이상 102 이하, 차는 7, 8, 9 중 하나여야 한다. 들어 맞는 조합은 (94, 93)밖에 없다.

다시 아래부터 빈 칸을 채우다 보면 백만의 자리에서 경우가 갈리게 되는데, 이 연산은 두 자리 수(o) – 두 자리 수(p)이고 차는 10이다. 가능한 o와 p의 조합은 (41, 31), (72, 62)이지만 천만의 자리 연산이 위 만의 자리 연산과 같으므로 가능한 조합은 (72, 62)뿐이다.

이로써 모든 칸을 채울 수 있다. 피제수는 1,002,324,327, 제수는 31, 몫은 32,333,042.80645이다.