머신러닝과 정보이론: 작동원리의 이해

정보량을 수치화 할 수 있을까? 1948년 벨 연구소의 클로드 섀넌^{Claude Shannon}은 “A mathematical theory of communication”이라는 제목의 논문을 발표한다.[1] 지금은 “The mathematical theory”가 된 정보이론은 디지털 통신의 이론적 토대를 구축했고, 수학, 통계학, 물리학, 생물학, 그리고 머신러닝에도 큰 영향을 미치고 있다. 이론물리학자 존 훨러^{John Wheeler}는 정보야말로 물질과 에너지보다 더 근본적인 우주의 실체라며, 유명한 문구 “it from bit”을 남긴 바 있다.[2] 이번 글에서는 정보이론의 핵심 개념을 간단히 짚어보고, 정보이론이 머신러닝의 작동원리를 설명하는 데 어떻게 쓰이는지 살펴보자.

^영상1 클로드 섀넌의 유튜브 영상 “Claude Shannon – Father of the Information Age”

섀넌의 정보이론에는 정보의 압축과 전달을 수치화한 엔트로피^Entropy와 상호정보량^{mutual information}이라는 두 가지 물리량이 등장한다.[3] 먼저 섀넌의 엔트로피를 살펴보자.¹ 두 가지 가능성을 가진 무작위 변수 \(X\)의 불확실한 정도를 수치화해보자. \(X=0\)인 확률이 \(p\)이고 \(X=1\)인 확률이 \(1-p\)인 경우, \(H(X) = – p \log p – (1-p) \log (1-p)\)는 \(X\)의 불확실성을 측정하는 하나의 좋은 물리량이 된다. \(p=0\) 또는 \(p=1\)인 경우, \(H(X)=0\)으로 불확실성이 없어지고, \(p=0.5\)인 경우, \(H(X)=1\) 비트^bit로 한 번의 질문이 필요한 불확실성이 생긴다.² 무작위 변수 \(X\)의 정보량 \(H(X)\)는 사실 정보의 합과 분리를 우리의 상식과 일치하도록 정의하는 유일한 선택이다. 두 가지 이상의 사건을 다루는 무작위 변수 \(X\)에 대한 엔트로피는 다음처럼 일반화된다.³
\begin{equation}
\tag{1}
H(X) = -\sum_x p(x) \log p(x) = \mathbb{E} \bigg[\log \frac{1}{p(x)} \bigg]
\end{equation}

여기서 \(\log (1/p(x))\)은 사건 \(x\)가 일어 난 경우 얻는 정보량으로 해석할 수 있다. 확률 \(p(x)\)가 큰 사건의 경우, 특별하지 않은 사건이어서 사건이 일어나도 얻게 되는 정보가 적을 것이다. 반대로 확률 \(p(x)\)가 낮은 사건의 경우, 사건이 일어나면 많은 정보를 얻을 수 있다. 가령, 개연성이 매우 높은 “내일 해가 뜬다”는 서술에는 매우 적은 정보가 들어 있지만, 개연성이 매우 낮은 “내일 해가 뜨지 않는다”는 서술에는 매우 많은 정보가 들어 있는 셈이다. 이렇게 해석을 하면 \(H(X)\)는 모든 사건에 대한 정보량의 기댓값인 평균 정보량이 된다.

다시 통신 문제로 돌아가면, 전달하려는 메시지의 코드가 바로 \(X\)에 해당한다. 효율적인 코드가 되기 위해서는 자주 주고받는 메시지는 가능하면 짧은 코드로 쓰고, 가끔 주고받는 메시지는 조금 긴 코드를 쓰면 될 것이다. 여기서 가장 효율적인 코드의 길이 \(l(x)\)는 사용하는 상대적인 빈도수 \(p(x)\)와 \(l(x) =\lceil \log (1/p(x)) \rceil\) 관계를 가진다.⁴ 섀넌은 아무리 좋은 코드를 설계하더라도 평균 길이가 엔트로피 \(H(X) = \sum_x p(x) l(x) = – \sum_x p(x) \log p(x)\)보다 짧아질 수 없음을 밝혔다.

이번에는 두 번째 정보량인 무작위 변수 \(X\)와 \(Y\) 사이의 상호정보량을 살펴보자.

\begin{eqnarray}
\tag{2}
I(X;Y) &=& H(X) – H(X|Y) \\
\tag{3}
&=& -\sum_x p(x) \log p(x) + \sum_{x,y} p(x,y) \log p(x|y) \\
\tag{4}
&=& -\sum_x p(x) \log p(x) + \sum_{x, y} p(x,y) \log \frac{p(x,y)}{p(y)} \\
\tag{5}
&=& H(X) + H(Y) – H(X,Y)
\end{eqnarray}

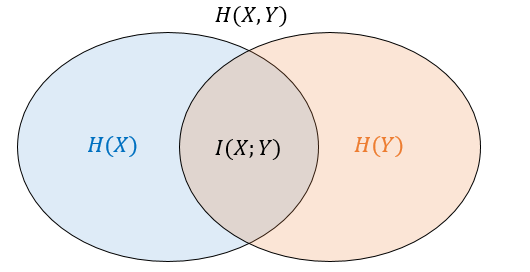
이는 \(X\)에 대한 불확실한 정도인 엔트로피 \(H(X)\)에서 \(Y\)가 주어진 경우 \(X\)에 대한 불확실한 정도 \(H(X|Y)\)를 뺀 정보량에 해당한다. 벤다이어그램으로 살펴보면 \(X\)와 \(Y\)가 겹치는 영역을 뜻한다.([그림2]) 일종의 상관관계인 셈인데, \(X\)와 \(Y\)는 역할을 바꿔도 같은 결과를 준다.

엔트로피와 상호정보량은 통신과정에서 일어나는 정보의 압축과 전달을 수치화하는 중요한 개념이 된다. 송신자가 보낸 코드 \(X\)가 수신자에게 \(Y\)라는 코드로 전달되는 통신을 생각해보자. 여기서 송신과 수신을 매개해주는 통로를 채널이라고 하는데, 채널을 통한 실제 통신과정에서는 정보의 손실과 왜곡이 불가피하게 일어난다. 채널에서 일어나는 정보전달의 불완전성은 송·수신 코드 사이의 확률적 관계 \(p(y|x)\)로 표현할 수 있다. 섀넌은 이렇게 불완전한 채널의 정보전달 용량^{channel capacity}은 상호정보량으로 수치화할 수 있음을 보였다.

\begin{equation}
\tag{6}
C= \max_{p(x)} I(X;Y)
\end{equation}
즉, 채널용량은 코드의 사용 빈도수 \(p(x)\)를 조정하면서 \(X\)와 \(Y\)사이에서 얻을 수 있는 최대 상호정보량으로 정의된다. 채널용량이 \(C=0\)인 채널은 어떤 정보도 전달하지 못하고, \(C=1\)인 채널은 1 비트에 해당하는 정보를 전달한다. 여기서 채널용량이 \(C\)라는 의미는, \(2^C\)개 만큼의 구별되는 메시지를 전송할 수 있는 채널이라는 뜻이다.

이번에는 채널용량과 쌍대성^duality이 있는 왜곡 비트율 이론^{rate distortion theory}을 살펴보자. 이는 통신에서 코드 \(X\)를 바로 전송하지 않고 압축된 코드 \(Z\)로 변환해서 전송하는 소스코딩과 관련된 이론이다. 특정 코드 \(x\)와 압축코드 \(z\) 사이의 왜곡 정도가 임의의 거리함수 \(d(x,z)\)로 정의되는 압축을 생각해보자. 섀넌은 정보의 평균 왜곡 \(\sum_{x,z} p(x,z) d(x,z) = D\)를 허락하는 \(X\)와 \(Z\) 사이의 왜곡 비트율 역시 상호정보량으로 표현할 수 있음을 보였다.

\begin{equation}
\tag{7}
R(D) = \min_{p(z|x)} I(X;Z)
\end{equation}
\(D\)만큼의 평균 왜곡을 허락하는 조건 아래에서, \(X \rightarrow Z\)의 변환 \(p(z|x)\)를 조정해서 \(X\)와 \(Z\) 사이의 상호정보량을 최대한 줄이는 최적화이다. 이렇게 하면 \(2^R\)개 만큼의 구별되는 메시지를 압축코드 \(Z\)를 통해서 표현할 수 있다.

여기서 왜곡이 전혀 없는 \(D=0\)인 경우를 살펴보자. 이는 \(Z\)로부터 \(X\)를 완전히 복원할 수 있어서 불확실한 정도 \(H(X|Z)=0\)이 된다. 이 조건 아래에서 왜곡 비트율과 섀넌의 엔트로피는 \(R(D=0)=H(X) – H(X|Z)=H(X)\)로 같다. 즉, \(H(X)\)가 왜곡이 없는 조건에서 코드 \(X\)의 정보량을 수치화했다면, 왜곡 비트율 이론은 왜곡을 허락하는 일반적인 조건에서 \(X\)가 압축된 코드 \(Z\)를 통해서 가지게 되는 정보량을 수치화해준다.

지금까지 설명한 채널용량과 왜곡 비트율 이론은 정보의 전달과 압축 사이의 균형을 개념화하는 정보이론의 두 가지 핵심 정리이다. 채널용량이 왜곡 수준이 정해진 채널을 통해 최대한 전달할 수 있는 정보량을 수치화한다면, 왜곡 비트율 이론은 원하는 수준의 정보전달을 확보하면서 최대한 압축 또는 왜곡할 수 있는 정보량을 수치화한다. 두 가지 정리 사이의 쌍대성에 대해서 좀 더 살펴보자.

먼저 왜곡 비트율 이론은 구별되는 총 메시지의 개수를 정해두고 각 메시지에 해당하는 코드를 가능한 많이 할당하는 과정이다. 하나의 메시지에 여러 코드를 할당함으로써 코드가 조금 왜곡되어도 같은 메시지를 복원할 수 있도록 만들어 준다. 즉, 전체 \(2^{H(X)}\)개의 코드 가운데, \(2^{H(X|Z)}\)개 만큼의 코드는 같은 메시지를 가리키는 경우, \(2^{H(X)}/2^{H(X|Z)} = 2^{I(X;Z)} = 2^R\)만큼의 구별되는 메시지를 표현할 수 있게 된다. 이는 자루에 담을 수 있는 공의 개수를 고정한 채로 공의 크기를 최대한 키우는 구체 덮음^{sphere covering} 문제에 해당한다. 여기서 각 공은 구별되는 메시지를 나타내고 공의 크기는 각 메시지에 할당된 코드의 개수에 해당한다. 그리고 자루의 크기는 가능한 모든 코드를 담고 있는 공간의 크기을 뜻한다.

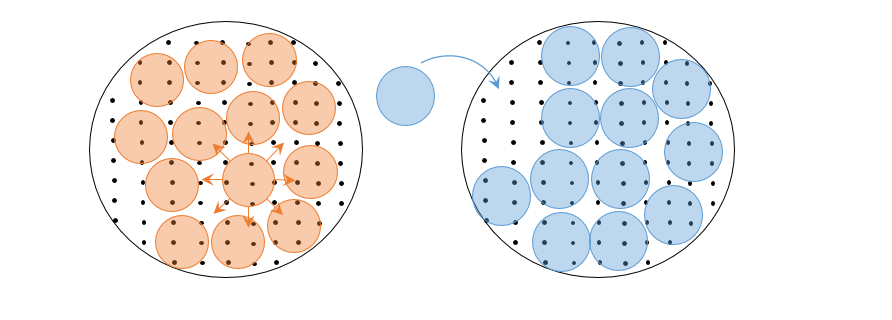
이번에는 채널용량을 살펴보자. 불완전한 채널을 통해 코드가 전달될 때, 어느 정도 왜곡이 불가피하게 일어난다. 왜곡의 수준을 알고 있는 채널에서 구별해서 전달할 수 있는 메시지의 최대 개수는 채널용량에 의해 결정된다. 전체 \(2^{H(X)}\)개 만큼의 구별되는 코드 가운데, 왜곡에 의해서 \(2^{H(X|Y)}\)개 만큼은 같은 메시지를 가리키는 경우, \(2^{H(X)}/2^{H(X|Y)} = 2^{I(X;Y)} = 2^C\)만큼의 구별되는 메시지를 전송할 수 있다. 앞서 얘기한 왜곡 비트율 이론에서는 \(H(X|Z)\)를 조정해서 \(R\)을 변화시켰다면, 채널용량은 왜곡정도인 \(H(X|Y)\)는 고정된 채로 \(H(X)\)를 조정해서 \(C\)를 변화시킨다. 이는 자루에 담는 공의 크기가 정해진 경우 담을 수 있는 공의 개수를 최대한 늘리는 구체 채움^{sphere packing} 문제에 해당한다. 구체 덮음과 구체 채움 문제는 자루에 담는 공의 크기와 개수 사이의 쌍대성 관계를 보여준다.([그림3])

이제 정보의 압축과 전달을 수치화할 수 있는 정보이론의 엔트로피와 상호정보량을 바탕으로 머신러닝에서 일어나는 정보흐름을 살펴보자. 1999년 나프탈리 티쉬비^{Naftali Tishby}, 페르난도 페레이라^{Fernando Pereira}, 윌리엄 비아렉^{William Bialek}은 지도학습에서 일어나는 정보의 흐름을 통신이론으로 해석한 정보병목이론^{information bottleneck theory}을 발표했다.[4] 이는 입력 \(X\)와 출력 \(Y\)가 주어진 문제에서 내적표현 \(Z\)를 통한 정보의 압축 \(I(X;Z)\)와 전달 \(I(Z;Y)\) 사이의 균형을 정의한 이론이다.

\begin{equation}
\tag{8}
\min_{p(z|x)} I(X;Z) – \beta I(Z;Y)
\end{equation}
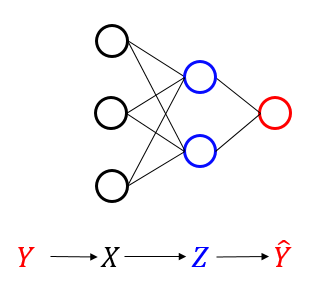
어떤 메시지 \(Y\)를 코드화한 것이 \(X\)이고, 이를 압축한 코드가 \(Z\)에 해당하고, 이를 디코딩한 \(\hat{Y}\)가 \(Y\)와 일치하게 되면 통신이 성공한 것으로 해석한다.([그림4])

즉, 지도학습은 은닉층의 압축된 표현 \(Z\)를 통해 라벨 \(Y\)를 전달하는데 필요한 정보만 남기고, 입력 \(X\)에서 불필요한 정보를 최대한 지우는 압축과정으로 해석한 것이다. 입력층에서 출력층으로 갈수록 좁아지는 구조를 가진 인공 신경망에서는 실제로 입력 \(X\)의 압축이 일어나고, 신경망은 압축된 \(Z\)를 통해서 실제 라벨 \(Y\)를 맞추는 학습을 하게 된다. 신경망을 통해 예측하는 라벨 \(\hat{Y}\)와 실제 라벨 \(Y\) 사이의 거리인 \(\|\hat{Y} – Y \|^2\)를 목적함수로 정의하고 이 거리를 좁혀가는 것이 지도학습이다. 하지만 일반적인 지도학습의 알고리즘 자체에는 \(I(X;Z)\)를 최소화하라고 하는 명령은 어디에도 없다. 그럼에도 불구하고 좁아지는 심층 신경망에서 정보의 효과적인 압축이 일어나고 있다는 사실이 신기하다.

한편 구글의 알렉스 아레미^{Alexander Alemi}와 동료들은 최근 변분추론^{variational inference} 방법을 이용해서 \(I(X;Z)\)를 직접 목적함수에 넣어서 최적화를 진행하는 심층-변분-정보병목 신경망^{deep variational information bottleneck}을 제안했고, 이에 대한 열역학적 해석을 내놓았다.[5] 

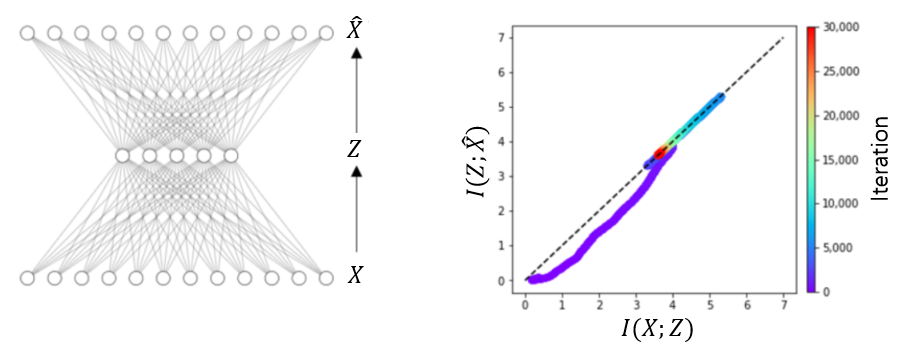
정보병목이론에서 \(I(X;Z)\)는 정보의 압축, 그리고 \(I(Z;Y)\)는 정보의 전달을 나타낸다. 여기서 정보의 전달을 나타내는 \(I(Z;Y)\)에서 실제 라벨 \(Y\) 대신에 신경망이 예측하는 라벨 \(\hat{Y}\)로 바꿔치기를 하면 학습과정 중 인공신경망에서 일어나고 있는 정보의 흐름을 시각화 할 수 있다.⁵ 2차원 평면에서 \(\big( I(X;Z), I(Z;\hat{Y}) \big)\)을 시각화해서 정보의 흐름을 분석하는 것을 정보평면^{information plane} 분석법이라고 부른다.[7] 정보평면 분석법에 따르면 지도학습 과정은 맞추기^fitting와 단순화^simplifying 과정으로 구성된다.([그림5])

그림에서 보여주는 예는 \(X\) 자체를 라벨 \(Y=X\)로 생각하는 자기지도학습^{self-supervised learning} 과정이다. 학습 초기에는 \(I(Z;\hat{X})\)를 키우는 맞추기 과정이 짧게 일어나고, 이후 \(I(X;Z)\)를 줄여서 맞추기에 필요없는 정보를 없애가는 단순화 과정이 꽤 오래 일어난다. 그리고 이 단순화 과정은 학습에서 보여주지 않았던 새 데이터에 대한 학습의 일반화와 관련이 있다고 보고 되었다.[7]. 하지만 학습의 일반화를 위해서 단순화 과정이 항상 필요한 것 같지는 않다. 일부 신경망에서는 단순화 과정이 일어나지 않고도 학습을 일반화하는 데 아무런 문제가 없는 경우도 있기 때문이다.[8]

이번에는 비지도학습 과정에서 일어나는 정보흐름을 살펴보자. 이전 글 “볼츠만 머신: 생성 모형의 원리”에서 소개했듯 비지도학습은 라벨 또는 메시지 \(Y\)가 주어지지 않은 데이터에서 \(X\)의 분포 자체를 학습하는 것이 목적이다. 데이터 \(X\)와 짝을 이룰 숨은 변수 \(Z\)를 도입하고, 이를 통해서 \(X\)의 분포를 학습하는 \(X-Z\) 구조의 신경망을 생각해보자.

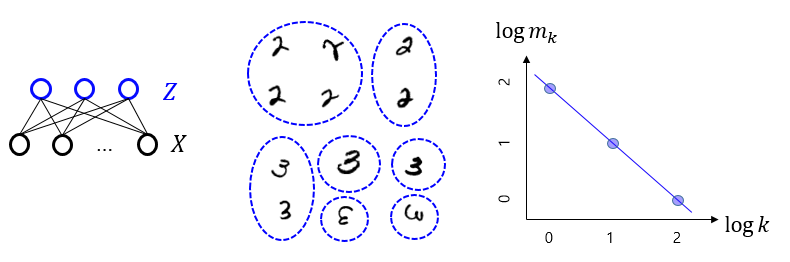
학습을 마치면 각 데이터 \(X\)는 해당 내적표현 \(Z\)를 가지게 된다. 가령, 손글씨 숫자 이미지들을 데이터로 사용했을 때는 각 이미지에 해당하는 \(Z\)가 얻어진다.([그림6]) 여기서 \(Z\)를 데이터 \(X\)에 대한 일종의 코드로 해석을 하면, 비지도학습은 코드를 통한 데이터 묶음^clustering으로 볼 수 있다.⁶ 만약 데이터 \(X\)에 대한 아무런 사전지식이 없다면, 우리는 같은 크기의 묶음들에 포함된 \(x\)들끼리는 다르게 볼 근거가 없다. 왜냐하면 우리는 \(x\)가 속한 묶음의 크기를 빼면 \(x\)에 대해서 아는 것이 아무것도 없기 때문이다. 이런 의미에서 \(z\) 묶음의 크기 \(k(z)\)는 비지도학습과정에서 창발한 일종의 라벨로 해석해 볼 수 있다.

이제부터 우리는 “자연스러운” 데이터 묶음을 생각해보려고 한다. 먼저 데이터 묶음의 구별정도는 다음과 같은 \(Z\)의 엔트로피로 정량화할 수 있다.

\begin{equation}
\tag{9}
H(Z) = -\sum_z \frac{k(z)}{M} \log \frac{k(z)}{M}= -\sum_k \frac{k m(k)}{M} \log \frac{k}{M}
\end{equation}여기서 전체 데이터의 개수는 \(M=\sum_z k(z) = \sum_k k m(k)\)이고, \(m(k)\)는 \(k\) 크기에 해당하는 묶음의 개수를 뜻한다. 그리고 \(2^{H(Z)}\)는 전체 묶음의 유효개수를 뜻한다. 이번에는 묶음의 크기의 다양성을 생각해보자. 이 경우 묶음의 크기 \(K\)의 불확실한 정도는 또 다른 엔트로피로 표현해볼 수 있다.

\begin{equation}
\tag{10}
H(K) = -\sum_k \frac{k m(k)}{M} \log \frac{k m(k)}{M}
\end{equation}묶음의 개수가 고정된 조건에서 가장 자연스러운 데이터 묶음이란 묶음 크기의 다양성 또는 불확실성을 최대화시키는 경우일 것이다. 이를 라그랑주 승수법으로 표현해보면 다음과 같다.

\begin{equation}
\tag{11}
\label{eq:hkhz}
\max_{m(k)} H(K) + \beta H(Z)
\end{equation}

이 최적화의 결과로 얻는 \(m(k) \sim k^{-\beta -1}\)는 묶음의 크기에 특별한 척도를 주지 않는 멱법칙을 따른다.⁷ 즉, 특별한 크기의 척도가 존재하지 않기 때문에 크기의 불확실성이 최대가 되고, 결국 크기의 다양성이 가장 커지게 되는 것이다. 비지도학습의 결과로 나타나는 묶음의 크기 분포 \(m(k)\)는 위 최적화의 결과인 멱법칙을 실제로 따른다.[9] 이는 비슷한 \(x\)들로 이루어진 큰 묶음이 꽤 있고, 개성이 강한 \(x\)들이 외따로 구분된 작은 묶음이 매우 많이 있는 분포이다. 흥미롭게도 비지도학습 알고리즘에는 내적표현 \(Z\)의 빈도수 또는 묶음의 크기에 대한 어떤 명령도 없었다는 것이다. 위 비지도학습의 최적화를 표현하는 식(11)는 표현을 조금 고쳐보면 통신이론의 채널용량을 나타내는 아래 식과 같음을 보일 수 있다.⁸

\begin{equation}
\tag{12}
\max_{p(z)} I(Z;K) + \beta I(X;Z)
\end{equation}

여기서 한 가지 주목할 점은 묶음의 크기 \(K\)가 비지도학습의 라벨 또는 통신의 메시지 \(Y\)와 같은 역할을 하고 있다는 것이다.

지금까지의 이야기를 정리해보면, 지도학습은 데이터의 라벨을 구별할 수 있는 수준에서 데이터의 압축표현 \(Z\)를 찾는 과정으로 생각할 수 있다. 그리고 비지도학습은 데이터의 압축정도를 정해놓고, 창발된 라벨인 데이터 묶음크기 \(K\)를 최대로 다양화하는 과정으로 생각할 수 있다. 지도학습과 비지도학습의 정보전달과 압축과정은 통신이론의 왜곡 비트율 이론과 채널용량과 닮은 구석이 있다. 왜곡 비트율 이론은 전달하는 메시지의 개수가 정해진 통신에서 메시지를 인코딩하는 코드를 최대한 압축하는 것이고, 채널용량은 정보전달의 왜곡 또는 정확도가 정해진 통신에서 구별되는 메시지의 개수를 최대로 늘리는 것으로, 왜곡 비트율 이론과 채널용량 사이에는 쌍대성이 있다.

이렇게 우리는 세 번의 연재를 통해서 머신러닝의 지도학습과 비지도학습을 살펴보았고, 이를 정보이론의 틀에서 이해해 보았다. 마지막 연재에서는 신경망을 쓰지 않고, 정보기하학을 이용해서 데이터사이언스를 하는 좋은 예제를 하나 소개해 보려고 한다.