코호몰로지cohomology 이론은 현대의 대수학, 기하학과 위상 수학의 연구에 쓰이는 가장 강력한 도구 중 하나다. 코호몰로지 이론이 이들 분야에 미친 영향은 실로 엄청나서, 대수학과 기하학의 역사는 코호몰로지의 사용 전후로 나뉠 수 있다고 해도 과언이 아닐 정도다. 하지만 이렇게 중요한 코호몰로지 이론은 대중에게는 잘 알려지지 않은 개념인데, 코호몰로지 이론을 설명하는 것이 굉장히 까다롭기 때문이다. 이번 HORIZON 글의 목적은 코호몰로지가 무엇인지를 가능한 한 쉽고 재미있게 알아보는 것이다. 수식적으로 완벽한 묘사보다는 되도록 역사적인 흐름 위주의 설명을 하려고 한다. 이것이 독자들에게 조금 더 부담 없게 와 닿길 바란다.
코호몰로지 이론은 아직도 끊임없이 발전하고 있는 이론이다. 지금 이 순간에도 수많은 수학자들이 밤낮으로 코호몰로지를 연구하고 있다. 1990년 후반 수학자 보에보드스키Voevodsky는 모티빅 코호몰로지motivic cohomology를 발견한 공로로 필즈상을 수상했고, 더욱 최근인 2016년 수학자 바트Bhatt와 숄츠Scholze는 프리즘 코호몰로지prismatic cohomology 이론을 창시해 각각 뉴 호라이즌상과 필즈상을 수상했다. 21세기 밀레니엄 7대 미해결 난제 중 하나인 호지 추측Hodge conjecture은 서로 다른 두 코호몰로지 이론이 어떻게 연관돼 있는지를 예측한다. 2022년에 필즈상을 수상한 허준이 교수님은 조합론의 문제들을 코호몰로지를 사용해서 접근한다.
코호몰로지 이론은 다양한 방식으로 해석될 수 있다. 이 글은 필자의 개인적인 수학적 배경과 이해를 바탕으로 두 개의 출판된 책 [1,3]을 풀어서 작성됐음을 알린다.
코호몰로지의 탄생
공간이란 무엇일까? 누군가 독자들에게 이 질문을 한다면 독자들을 과연 어떻게 대답할 것인가? 많은 수학자들의 노력 끝에 현대 수학은 이 질문에 대한 만족스러운 답변을 찾았다. 그리고 코호몰로지 이론은 수학자들이 이 질문의 답을 찾는 과정에서 발견됐다.
고전적인 기하학은 평면 위의 직선, 삼각형이나 원 등의 성질을 연구하는 학문으로, 종종 유클리드 기하학Euclidean geometry이라고도 불린다. 유클리드 기하학은 기원전부터 무려 2000년 동안이나 절대적인 기하학으로 군림했다. 1600년 중반 데카르트가 좌표계를 도입하고, 1600년 후반 뉴턴과 라이프니츠가 미적분학을 개발했으며, 1700년 중반 오일러가 휘어진 곡면을 연구하기 시작할 때도 아무도 유클리드 기하학에 의문을 제기하지 않았다. 이러한 유클리드 기하학에 대한 믿음이 깨지기 시작한 것은 1800년 초였다. 이 시기는 가우스가 곡면의 곡률에 대한 연구를 하며 그의 유명한 “놀라운 정리Theorema egregium“를 막 발표하던 시기였다. 이 정리는 당시 매우 파격적이었는데, 왜냐하면 이것이 유클리드 기하학과 전혀 다른 기하학이 존재할 가능성을 암시하고 있었기 때문이다. 완전히 새로운 기하학이 탄생할 시대적 상황이 무르익고 있었다.
1830년경, 로바체프스키Lobachevsky를 비롯한 몇몇 수학자들이 거의 동시에 기존의 유클리드 기하학에 반하는 비유클리드 기하학을 발견한다. 이것은 기념비적인 발견이었으나 동시에 혼란을 야기했다: 유클리드 공간이 절대적 공간이 아니라면, 도대체 공간이란 무엇인가? 1850년경, 수학자 리만이 이 문제에 대한 철학적 해답을 제시하며 기하학의 현대화가 시작됐다. 리만은 유클리드나 비유클리드 공간 역시 더 일반적인 개념의 공간의 특수한 경우에 지나지 않는다고 생각했다. 따라서 공간이 무엇인지를 정확히 이해하라면 역설적으로 더욱 일반화된 공간을 공부해야 한다는 것이다. 리만의 아이디어는 매우 획기적이었으나 기술적으로 상당히 복잡해 당시에 완벽하게 수용되지 못했다. 1896년, 마침내 푸앙카레Poincaré가 리만의 아이디어를 가다듬어 현대적인 개념의 \(n\)차원 공간manifold을 명확하게 정의한다. 기하학이 유클리드 공간에서 해방된 것이다!
푸앙카레의 \(n\)차원 공간을 수학적으로 정확하게 설명하는 것은 이 글의 요지와 맞지 않는다. 다만 직관적으로, 우리는 하나의 공간 \(X\)를 하나의 우주와 같다고 생각할 수 있다. 다시 말해 수학자들은 이론적으로 무한히 많은 \(n\)차원 우주(공간)을 생각하는 것이 가능하다. 하나의 새로운 \(n\)차원 공간 \(X\)마다 그 안에서 직선, 삼각형과 원을 똑같이 그려 기하학을 펼 수 있다. 하지만 이곳의 기하학은 기존의 유클리드 직관과는 다른 새 법칙에 의해 지배받는다.
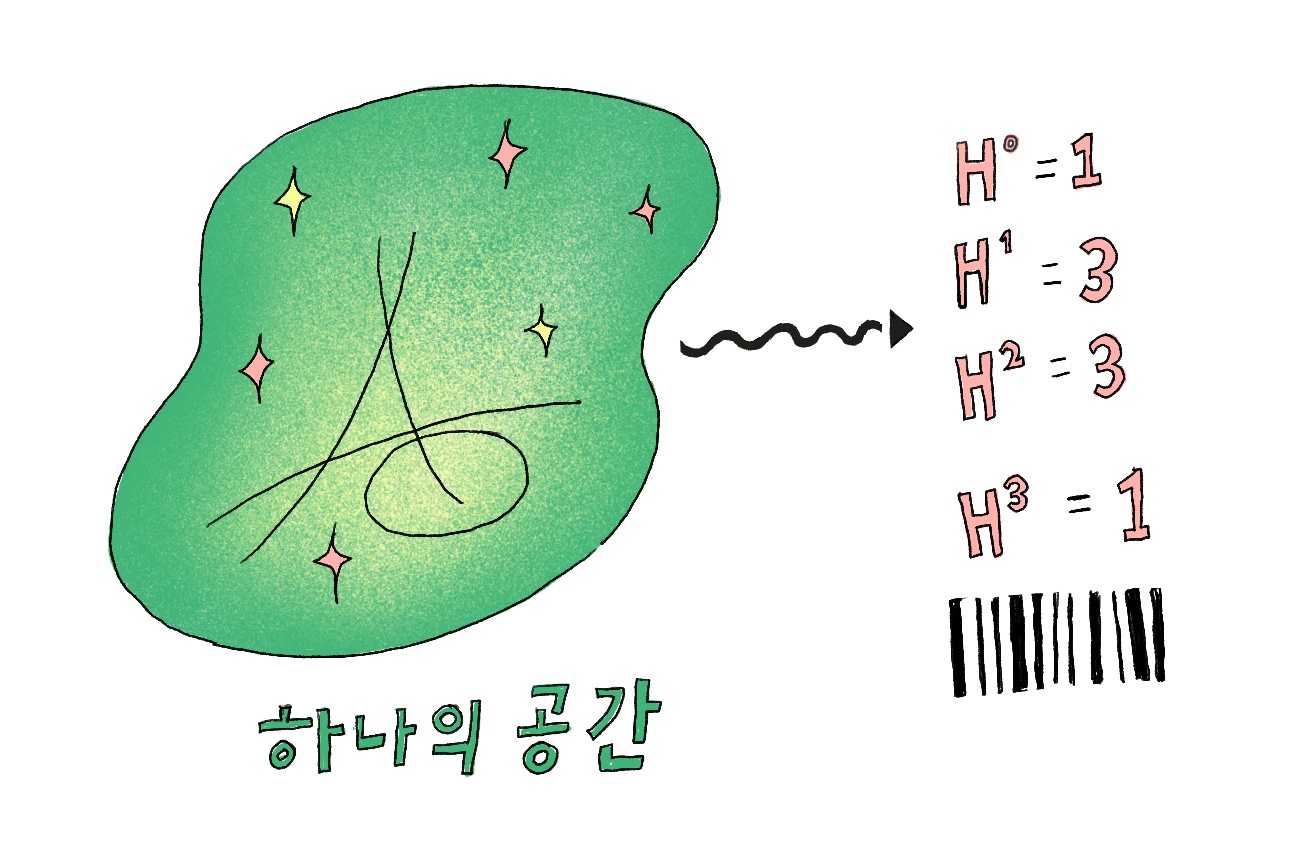
바로 이 순간 우리의 주인공 코호몰로지가 등장한다. 푸앙카레는 공간이란 개념을 정립하는 데 그치지 않고, 각각의 공간 \(X\)마다 특정한 숫자들을 도출할 수 있음을 깨달았다. 이 숫자들은 각각의 새로운 공간 \(X\)의 특징을 묘사하는 바코드와 같았다. 이것이 역사상 최초의 코호몰로지다.1 예를 들어, 동그란 원으로 이루어진 1차원 공간은 두 개의 숫자 \([1, \, 1]\)에 의해 그 특징이 설명된다. 지구 표면과 같은 2차원 공간은 세 개의 숫자 \([1, \, 0, \, 1]\)로, 도넛의 표면으로 이루어진 2차원 공간은 \([1, \, 2, \, 1]\)로 묘사될 수 있다. K3공간으로 알려진 특정 4차원 공간은 다섯 개의 숫자 \([1, \, 0, \, 22, \, 0, \, 1]\)에 의해 묘사된다.
푸앙카레는 이 숫자들이 앞뒤로 완벽하게 대칭이라는 사실 또한 알아차렸다. 독자들 또한 위의 수열들이 모두 앞뒤로 대칭이라는 점을 확인할 수 있을 것이다. 이것이 코호몰로지의 신비한 성질을 보여주는 첫 번째 정리로, 오늘날 우리는 이것을 푸앙카레 쌍대 정리Poincaré duality라고 부른다. 수학자들은 즉시 푸앙카레의 새로운 공간과 숫자들의 발견에 고무됐다. 이 숫자들은 분명히 깊은 의미를 지니고 있었다. 하지만 이 숫자들을 이해하는데 100년이 넘는 세월이 걸릴 것이라고 생각한 사람은 아무도 없었다.
코호몰로지의 초기 발전
앞선 내용을 정리해보자. 1900년경 푸앙카레는 무한히 많은 \(n\)차원 공간들을 수학적으로 정의한다. 그는 곧장 각각의 \(n\)차원 공간 \(X\)의 특성을 묘사하는 \(n+1\)개의 숫자들이 있음을 발견한다. 이 숫자들이 훗날 수 많은 수학자들의 머리를 쥐어뜯게 만든 코호몰로지 이론의 전신이다. 우리는 앞으로 코호몰로지가 단순한 숫자들의 나열보다 훨씬 더 깊은 의미를 가짐을 살펴볼 것이지만, 이 숫자들을 코호몰로지의 가장 간단한 버전이라고 생각해도 크게 문제 될 것은 없다.
코호모롤지 (첫 번째 설명).\(n\)차원 공간 \(X\)의 코호몰로지란 이 공간의 특성을 묘사하는 \(n+1\)개의 숫자 \(H^0(X)\), \(H^1(X)\), \(\cdots\), \(H^n(X)\)를 의미한다.
예를 들어서, 곡면은 2차원 공간이므로 세 개의 코호몰로지 \(H^0\), \(H^1\), \(H^2\)를 가진다. 곡면의 0번째와 두 번째 코호몰로지 \(H^0\), \(H^2\)는 항상 1이 되어 큰 의미를 지니지 못한다. 곡면의 첫 번째 코호몰로지 \(H^1\)을 계산하면 항상 짝수 \(2g\)가 되는데, 여기서 \(g\)는 수학자들이 기존에 종수genus라고 부르던 곡면 \(X\)에 뚫린 “구멍의 개수”와 정확히 일치하게 된다.
다시 본론으로 돌아와서, 푸앙카레의 새로운 기하학과 코호몰로지 이론은 곧바로 수학자들의 비상한 관심을 끌었다. 그리고 이는 곧 위상 수학topology이라는 새로운 분야의 탄생으로 이어진다. 이후 거의 50년간 코호몰로지 이론은 위상 수학자들에 의해 발전된다. 이 시기에 발견된 코호몰로지에 대한 몇몇 중요한 사실들을 살펴보자.
- 1920년 중반, 뇌터Emmy Noether는 코호몰로지 \(H(X)\)가 사실 숫자들이 아닌 아벨군abelian group으로서 이해돼야 한다는 것을 발견한다. 푸앙카레가 발견한 숫자들은 이 아벨군들의 차원rank을 의미했다. 이때부터 수학자들은 코호몰로지가 단순한 숫자들보다 더 깊은 의미를 지닌다는 것을 깨달았다.
- 1930년 드람de Rham이 미적분학에서 이미 중요하게 사용되던 개념인 미분 형식differential form이 코호몰로지적 해석을 지님을 발견했다. 즉, 코호몰로지를 사용하면 기존의 이론을 새롭게 해석하는 것이 가능했다.
- 1930년 중반, 위트니Whitney와 체흐Čech에 의해 코호몰로지에 곱셈 구조가 존재함이 발견됐다. 이것은 코호몰로지가 아벨군보다 더 나아가 환ring으로서 해석돼야 함을 의미했다.1940년 중반, 아일렌버그Eilenberg와 스틴로드Steenrod가 알려진 많은 코호몰로지들을 통합하면서 코호몰로지 이론을 거의 완성시키는 것처럼 보였다.
이 시기를 거치며 점차 수학자들은 코호몰로지가 대수학적 개념2으로서 이해돼야 함을 깨닫는다. 다시 말하면, 코호몰로지 \(H(X)\)는 공간 \(X\)의 위상적 성질을 대수학적으로 해석하는 방법이었던 것이다. 마지막의 아일렌버그-스틴로드의 정리는 매우 아름다워 당시 많은 수학자들이 이것이 코호몰로지 이론을 완성시켰다고 생각했다.3 불행하게도 이 성취는 그리 오래 지속되지 못했다.
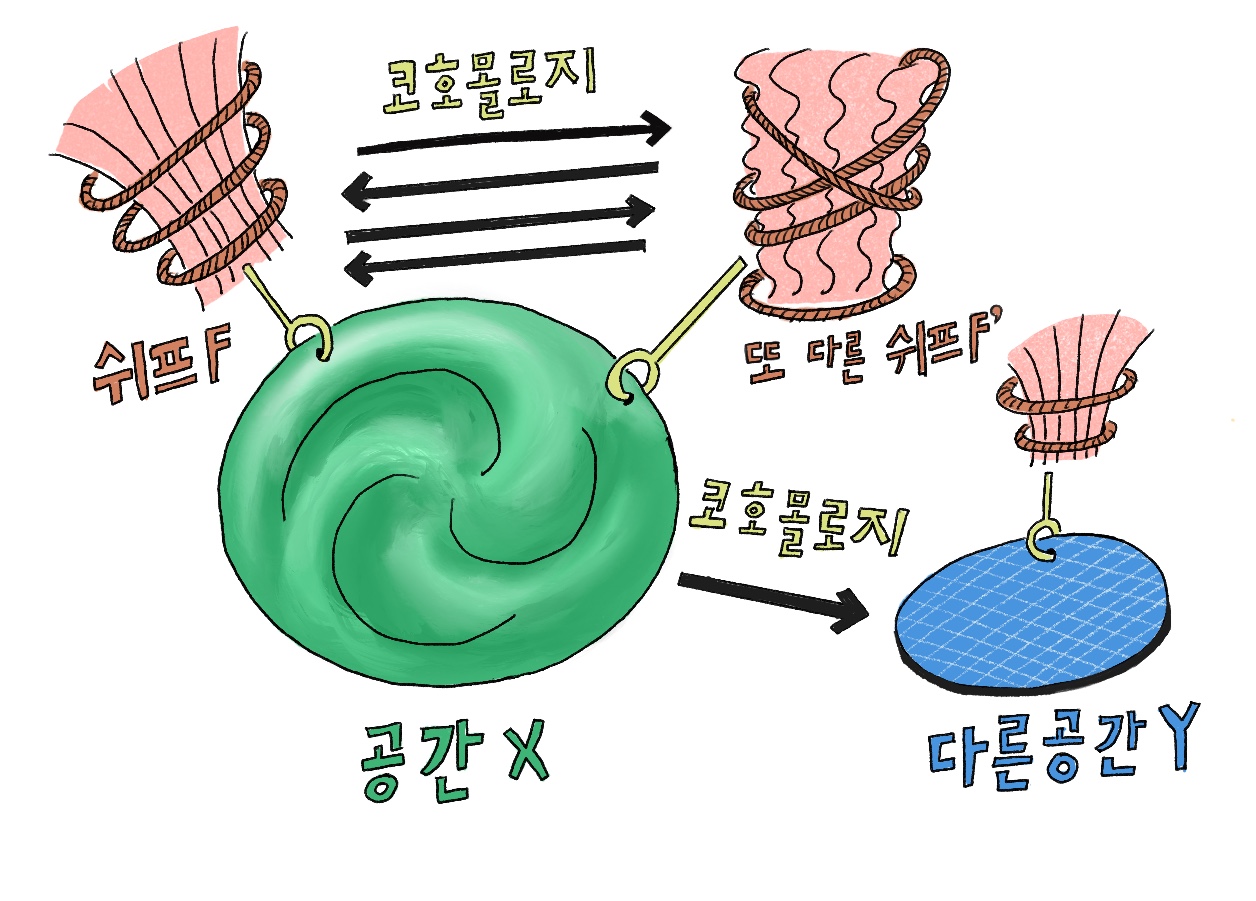
수학자 르레이Leray는 2차 세계 대전의 전쟁 포로로 1940년부터 5년 동안이나 감옥에 수감되며 세상과 단절돼 있었다. 하지만 그는 감옥에서 당시의 코호몰로지 이론을 뒤집을 새로운 관점을 발견한다. 르레이는 코호몰로지가 공간 \(X\)만의 성질을 묘사하는 것이 아니라고 생각했다. 그는 코호몰로지가 공간 \(X\)와 이 공간에 살고 있는 쉬프sheaf의 성질을 동시에 묘사하는 것이라는 것이라고 생각했다. 임의의 \(n\)차원 공간 \(X\)와 그에 달린 임의의 쉬프 \(F\)에 대해서도 똑같이 코호몰로지 \(H(X, F)\)를 정의할 수 있다는 것이다.4 르레이는 전쟁이 끝난 직후 이 결과를 세상에 발표했고, 이는 아일렌버그-스틴로드의 철학을 비롯한 이전 코호몰로지에 대한 수학자들의 이해를 원점으로 되돌렸다. 르레이의 쉬프 코호몰로지가 기존의 코호몰로지 이론을 박살내 버린 것이다.
한편 이렇게 코호몰로지 이론의 핵심에 대한 연구가 이루어지는 동안, 몇몇 다른 수학자들이 코호몰로지 이론을 자신의 분야에 적용해 보기 시작했다. 결과는 대성공으로, 코호몰로지는 기존의 어려운 문제들을 항상 마법처럼 간단하게 풀어내곤 했다. 코호몰로지 이론이 점차 널리 알려지며 그 중요성이 나날이 커지고 있었다. 하지만 수학자들은 정작 코호몰로지가 무엇인지 정확하게 설명하지는 못했다.
너무 많은 코호몰로지 이론
푸앙카레가 최초로 원시적 코호몰로지를 발견한 이후 이 개념을 확장하기 위한 수많은 노력이 이뤄졌다. 1950년을 전후로 르레이, 카르탕Cartan과 아일렌버그 등이 코호몰로지에 대한 중요한 결과들을 연이어 발표했고 이 시기를 기점으로 코호몰로지 이론이 폭발적으로 성장한다. 이러한 발전에도 불구하고 수학자들은 코호몰로지가 무엇인지 한 마디로 설명할 수는 없었다. 다만 경험적으로 이것이 대수학적 객체여야만 한다는 것은 분명해 보였다.
코호몰로지 (두 번째 설명). 공간 \(X\)의 코호몰로지란 이 공간의 특성을 묘사하는 대수학적 객체 \(H(X)\)를 의미한다.
하지만 이쯤해서 예측하지 못한 새로운 문제점이 대두되기 시작했다. 변종 코호몰로지들이 발견되기 시작한 것이다.5 처음에는 단 하나의 새로운 코호몰로지 이론을 발견하는 것만으로도 굉장한 발견이었으나 차츰 더 많은 코호몰로지가 발견되기 시작해 열 개, 스무 개의 코호몰로지 이론이 우후죽순 생겨났다. 이렇게나 많은 코호몰로지가 존재하는 것은 이상했다. 아일렌버그-스틴로드와 르레이의 철학이 이 문제를 일부 해결할 수 있었지만, 그럼에도 설명되지 않는 코호몰로지가 있었다.
1900년 중반과 후반을 거치면서 코호몰로지 이론은 위상 수학뿐만 아니라 기하학과 대수학 전 분야에서 광범위하게 사용되는 도구가 되고 있었다. 상황은 이전보다도 악화(?)되어 더욱 기상천외한 코호몰로지 이론들이 등장하기 시작했다. 이 시기에 발견된 중요한 코호몰로지들 중 몇 가지를 살펴보자.
- 1960년 그로센딕Grothendieck은 새로운 코호몰로지인 에탈 코호몰로지étale cohomology를 정의하며, 동시에 이것이 갈루아 표현Galois representation이라는 완전히 새로운 구조를 가진다는 것을 발견했다. 즉, 코호몰로지는 기존에 생각했던 것보다 더욱 정교한 대수학적 구조를 가졌다.
- 1950-1970년 차우Chow, 풀턴Fulton과 맥피어슨MacPherson이 차우 군Chow group이라는 새로운 코호몰로지를 개발한다. 차우 군은 무한 차원을 가지는 코호몰로지다.
- 1970-80년 들린Deligne과 그리피스Griffiths가 서로 다른 두 개의 코호몰로지 이론을 융합하면 하나의 새로운 코호몰로지 이론처럼 작동한다는 것을 발견했다. 이를 코호몰로지가 호지 구조Hodge structure를 가진다고 한다.
- 1980년 고레스키Goresky와 맥피어슨이 교차 코호몰로지intersection cohomology를 정의한다. 교차 코호몰로지는 특이점singularity을 가지는 공간에서 기존의 코호몰로지보다 더 잘 작동했다.
1900년 후반에 들어서자 수십 개가 넘는 코호몰로지 이론이 각기 다른 곳에서 쓰이고 있었다. 더 이상 모든 코호몰로지 이론을 알고 있는 수학자는 없었다. 왜 이렇게 많은 코호몰로지가 존재 해야 하는 것인가? 이것은 수학자들이 해결해야 할 또 다른 딜레마가 되었다. (독자들도 이쯤 되면 머리가 아파올 것이다.) 이를 해결하기 위해 우리는 코호몰로지 이론을 생각하는 현대적 관점으로 들어가게 된다.
현대의 코호몰로지
우리는 앞서 코호몰로지 이론이 굉장히 강력한 이론이기는 했지만, (1) 수학자들은 코호몰로지가 정확히 무엇을 의미하는지 이해하지 못했고, (2) 코호몰로지 이론의 범람이 수학자들을 더욱 혼란스럽게 만들었음을 살펴보았다. 그럼에도 불구하고 코호몰로지는 점차 수학의 여러 분야에 중요하게 사용돼 오늘날 더 이상 없어서는 안될 도구로 자리 잡게 된다.
오늘날의 수학자들은 코호몰로지가 가진 이 문제들을 어떻게 설명하고 있을까? 먼저 지나치게 많은 코호몰로지 이론이 존재하는 이유를 수학자들은 다음과 같이 설명한다.
범 코호몰로지 이론. 각각의 공간 \(X\)마다 단 하나의 범 코호몰로지 이론motive이 존재하며, 지금까지 발견된 나머지 모든 코호몰로지들은 이 범 코호몰로지를 다양한 각도에서 비춘 그림자를 관찰한 것이다.
이 멋진 아이디어는 현존하는 모든 코호몰로지 이론들을 단 한 번에 설명할 수 있을지도 모르지만, 아쉽게도 아직까지는 가설으로 남아있다. 1990년 말 보에보드스키를 비롯한 몇몇 수학자들이 이 범 코호몰로지 이론을 부분적으로 실현하는 데 성공했다. 그러나 아직도 넘어야 할 산들이 많이 남아있다. 이를 가로막고 있는 큰 관문들 중 하나가 바로 호지 추측으로, 이는 밀레니엄 7대 미해결 난제 중 하나다.
그렇다면 기존의 코호몰로지 이론들이 수학의 많은 분야에서 잘 작동하고 있는데, 굳이 코호몰로지 이론의 발전/통합에 집착해야 하는 이유가 무엇일까? 첫 번째 이유는 수학적 개념의 통합을 향한 수학자들의 순수한 도전 정신이다. 두 번째, 조금 더 실질적인 이유는 이것이 많은 미해결 난제들을 해결할 것으로 기대되기 때문이다. 하나의 수학 문제를 해결하는 것을 단단한 바위를 깨는 것에 비유한다면 코호모로지 이론은 공사용 드릴에 비유할 수 있다. 코호몰로지 이론의 발전은 수학자들이 더욱 강력한 드릴을 사용하는 것과 같다. 이것은 역사적으로도 여러 번 증명된 바 있다.
- 1982년 베일린슨Beilinson, 베른슈타인Bernstein과 들린은 교차 코호몰로지 이론을 발전시킨 퍼버스 쉬프perverse sheaf 이론을 개발한다. 퍼버스 쉬프의 개발로 분해 정리decomposition theorem가 발견되고 푸앙카레 쌍대 정리가 일반화된다.
- 1988년 사이토Morihiko Saito는 기존의 호지 구조를 발전시킨 호지 모듈Hodge module 이론을 개발한다. 호지 모듈을 사용으로 리만-힐버트 문제Riemann-Hilbert problem가 완전히 이해된다. 또한 고다이라 소멸 정리Kodaira vanishing theorem와 분해 정리가 일반화된다.
- 2000년 보에보드스키는 차우 군을 발전시킨 모티빅 코호몰로지를 개발한다. 모티빅 코호몰로지를 사용하여 밀너 추측Milnor conjecture과 블럭-카토 추측Bloch-Kato conjecture이 증명된다.
- 2016년 바트와 숄츠가 에탈 코호몰로지, 크리스탈 코호몰로지crystalline cohomology와 드람 코호몰로지를 융합한 프리즘 코호몰로지를 개발한다. 프리즘 코호몰로지를 사용하여 고다이라 소멸 정리가 혼합 표수mixed characterisitc 위로 일반화된다.
마지막으로, 오늘날 수학자들은 코호몰로지 이론을 어떤 식으로 설명하고 있을까? 현대의 코호몰로지 이론은 보통 카테고리 이론category theory을 사용하여 해석된다. 카테고리 이론은 기존의 집합론을 한 번 더 발전시킨 일종의 새로운 도약으로, 이를 사용하면 서로 다른 수학적 객체들의 상호 관계를 이해하는 것이 가능하다. 다만 카테고리 이론은 아직까지 수학의 모든 분야에 완벽히 흡수되지 못했다. 모든 급진적인 이론들이 그렇듯, 시간이 지나면서 카테고리 이론 또한 표준적인 방법으로 받아들여질 것이다.
코호몰로지 (세 번째 설명). 공간 \(X\)의 코호몰로지란 이 공간에 달린 모든 쉬프들의 상호 작용을 묘사하는 카테고리 \(H(X)\)를 의미한다.
사실 코호몰로지를 한 문장으로 설명하는 것은 쉽지 않다. 우리는 역사적인 관점에 따라 코호몰로지가 무엇인지를 세 단계에 걸쳐 설명하고자 했다. 이것이 독자들을 얼마나 납득시킬 수 있었는지는 잘 모르겠다. 하지만 독자들도 이제 이 신비로운 이론을 설명하는 것이 단순한 문제가 아니라는 것을 깨달았을 것이다. 필자도 처음 코호몰로지를 배웠을 때가 있었다. 책을 읽고 또 읽어도 이해가 되지 않았는데, 사실 다른 사람들도 똑같이 이해를 하지 못 하고 있어서 안심했던 기억이 있다. 도대체 코호몰로지는 무엇일까? 오늘날에도 새로운 수학자들이 바통을 이어받아 이 문제에 끊임없이 도전하고 있다. 수학자 힐버트가 말하길: 우리는 알아야만 한다. 우리는 알게 될 것이다!
참고문헌
- Jean Dieudonné. A history of algebraic and differential topology. 1900–1960. Birkhäuser Boston, Inc., Boston, MA, 1989.
- Paul Halmos. Picture of Jean Leray. University of St Andrews.
- Charles A. Weibel. History of homological algebra. In History of topology, pages 797–836. North-Holland, Amsterdam, 1999.
- Wikipedia. Genus (mathematics).
- Andrew Wiles. Modular elliptic curves and Fermat’s last theorem. Ann. of Math. (2), 141(3):443–551, 1995.