믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부

There is a theory which states that if ever anyone discovers exactly what the Universe is for and why it is here, it will instantly disappear and be replaced by something even more bizarre and inexplicable. There is another theory which states that this has already happened.
– Douglas Adams <The Restaurant at the End of the Universe> –

과학자의 강연에 참석하는 청중의 수에는 대략적인 최대치가 있다. 전공 강연이라고 하면 대개 50명 내외일 것이고, 대중 강연이라고 해도 200명을 넘기 힘들 것이다. 그런데 최근(2018년 8월 25일)에 필자가 1천 명이 넘는 청중 앞에서 강연할 일이 생겼다.

그 강연은 “카오스 재단^{KAOS foundation}”에서 매년 정기적으로 진행하는 “카오스 콘서트^{KAOS concert}”라는 대중 강연이었다. 카오스 콘서트는 매년 한 가지 주제를 중심으로 3명 내외의 강연자가 각자 자신의 전문 분야의 관점에서 해당 주제에 대해서 얘기를 하는 구조, 즉 그야말로 “강연으로 하는 콘서트”라는 구조로 되어 있다. 주제는 전적으로 수학 및 과학에 대한 내용인데, 필자가 이번에 참여하게 된 강연 콘서트의 주제는 “세상 모든 것을 설명하는 이론이 과연 가능한가?”라는 질문이었다. 구체적으로 강연 콘서트의 공식 제목은 “수학과 과학 42”였다.

왜 제목에 생뚱맞게 42가 들어가는지 궁금한 독자가 있을 것이다. 42를 전체적인 하나의 숫자로 생각하지 않고 4와 2를 따로따로 띄어서 읽으면 “사이”가 될 것이다. 그렇게 읽으면 콘서트의 제목은 “수학과 과학 사이”가 된다. 따라서 본 제목은 어찌 보면 수학과 과학 사이의 관계에 대해서 얘기하는 것이고, 또 다르게 보면 수학과 과학 사이 그 어딘가에 답이 존재하게 될 궁극의 질문(“세상 모든 것을 설명하는 이론이 과연 가능한가?”)에 대한 것이기도 하다. 그런데 왜 평범하게 “사이”라고 하지 않고 굳이 장난스럽게 42라고 했을까?

그 이유는 42가 바로 “삶, 우주, 그리고 모든 것의 궁극적인 질문에 대한 답^{Answer to the Ultimate Question of Life, the Universe, and Everything}”이기 때문이다. 필자를 믿지 못하겠다면 증거를 대겠다. 증거는 더글라스 아담스^{Douglas Adams}라는 작가가 쓴 <은하수를 여행하는 히치하이커를 위한 안내서 The Hitchhiker’s Guide to the Galaxy>라는 소설에 담겨있다. 혹시 이 소설에 대해서 전혀 들어 본 적이 없는 독자가 있는지 모르겠다. 솔직히 필자는 이런 독자가 부러운 마음마저 든다. 이는 마치 아주 재미있는 영화가 하나 있는데, 아직 이 영화를 보지 못한 사람에게는 그의 인생에 있어서 큰 즐거움 하나가 고스란히 남아 있는 상황과 같기 때문이다.

나중에 동명의 영화(영화는 소설에 비해서 약간 실망스럽다는 평이 있다)로도 만들어진 이 소설의 줄거리는 대략 다음과 같다. 소설과 영화 모두 예전(각각 1979년과 2005년)에 쓰이고 만들어졌지만 스포일러 경고를 하고 시작한다. 어느 목요일 아침 우리의 주인공 아서 덴트^{Arthur Dent}에게 그의 집을 허물고 우회도로^bypass를 건설해야 한다며 공사 인부들이 들이닥친다. 아서는 이를 막기 위해서 불도저 앞에 눕게 되는데, 어디선가 그의 친구인 포드 프리펙트^{Ford Prefect}가 다가와서 그보다 더 중요한 일이 있으니 술집에 가서 술이나 한 잔 하자고 설득한다. 포드는 술집에서 아서에게 사실은 자신이 외계인이며 잠시 후면 세계가 멸망할 것이라고 알려 준다. 그리고 지구는 포드의 말처럼 곧 파괴된다. 지구는 초공간 고속도로^{hyperspatial express route}를 만들기 위해서 보곤^Vogon이라고 불리는 외계인 종족에 의해 파괴된 것이다. 다행히도 포드는 아서와 함께 지구가 파괴되기 바로 직전에 보곤 족의 우주선에 히치하이크를 해서 지구를 탈출할 수 있었다. 이때 포드는 아서에게 본인이 “은하수를 여행하는 히치하이커를 위한 안내서”의 완성을 위해서 일하고 있는 연구원인데, 우연한 기회로 지구에 15년이나 머무르게 되었다고 알려 준다.

그런데, 지구가 파괴된 것은 어떤 이들을 매우 화나게 만들었다. 물론 지구에 살고 있던 지구인들은 매우 화가 났겠지만, 지구 파괴에 2분밖에 소요되지 않았기 때문에 화가 난 시간은 그리 길지 않았다. 그보다도 길게 화가 난 이들은 바로 초지능을 지닌 범차원적인 존재^{hyper-intelligent pan-dimensional being}였다. 그들은 아주 오래전에 “깊은 생각^{Deep Thought}”이라고 불리는 컴퓨터를 만들어서 “삶, 우주, 그리고 모든 것의 궁극적인 질문에 대한 답”을 얻기 위한 계산을 시켰다. 그리고 계산 결과로 나온 답이 바로 42였다.

물론 궁극적인 질문에 대한 답이 왜 하필이면 42인지는 초지능을 지닌 범차원적인 존재조차도 이해할 수 없었다. 그래서 왜 답이 42인지 물었더니 “깊은 생각”이 말하길 “질문을 제대로 하면 왜 답이 42인지 알게 될 것이다”라고 설명했다. 그리고 여기에 덧붙이기를, 자신보다 더 성능이 좋은 컴퓨터를 만들어 계산을 시키면 왜 42가 답인지 알 수 있는 제대로 된 질문을 얻을 수 있을 것이라고 했다. 그렇게 해서 초지능을 지닌 범차원적인 존재는 “깊은 생각”의 제안에 따라서 새롭게 컴퓨터를 만들게 되었는데, 그 컴퓨터는 크기가 매우 컸을 뿐만 아니라 생체 부품^{biological component}을 썼기 때문에 자주 행성^planet으로 혼동되고는 했다. 그 컴퓨터는 다름 아닌 지구였다. 그런데 그 지구가 지난 1천만 년 동안 진행된 계산을 최종적으로 완성하기까지 5분만을 남겨 놓은 상황에서 파괴된 것이다. 당연히 지구의 파괴는 초지능을 지닌 범차원적인 존재를 매우 화나게 만들었다. (그 이후에 벌어지는 일에 관해서는 독자들이 꼭 책이나 영화를 찾아서 보고 알아내기를 바란다.)

이제 본론으로 돌아가서, 필자가 강연자로 참여한 카오스 콘서트의 주제를 “은하수를 여행하는 히치하이커를 위한 안내서”의 스타일로 풀어보면, 그것은 “삶, 우주, 그리고 모든 것의 궁극적인 질문에 대한 답을 주는 이론이 과연 가능할까?”가 될 것이다. 지금까지 필자나 더글라스 아담스의 농담을 진지하게 받아들이는 독자는 없었을 테지만, 만약에 42가 답이라면 42가 답인 이유를 말해주는 이론이 과연 가능할까?

많은 수학자들은 수학 자체가 바로 그 궁극적인 이론이라고 생각할 것이다. 많은 물리학자들은 물리학, 그중에서도 특히 양자역학이 바로 그 궁극적인 이론이라고 생각할 것이다. 반면에 일부 물리학자를 포함해서 일군의 과학자들은 양자역학이 물질 세계를 다루는 궁극적인 이론이라는 데는 이견이 없지만, 양자역학에서 실제로 중요한 것은 “정보^information”이고, 정보가 궁극적인 답이라고 생각한다. 실제로 “양자 정보^{quantum information}”라는 분야가 있다. 이번 카오스 콘서트의 강연은 이러한 세 가지 관점의 충돌이었다. 아니, 적어도 그렇게 기획되었다.

이번 카오스 콘서트의 강연자는 필자와 카이스트 물리학과의 정하웅 교수님, 그리고 옥스퍼드대학교 수학과의 김민형 교수님이었다. 혹시 예상한 독자가 있을지 모르겠지만, 필자의 강연 제목은 본 연재글과 같은 이름을 가진 “Incredible Quantum”이었다. 어찌 보면 본 연재글을 진행하면서 다루게 될 내용의 일부를 미리 압축해서 강연한 것과 같다. “믿기 힘든 양자”가 앞으로 어떻게 전개될지 궁금한 독자가 만약에 필자의 강연을 들었다면 예고편을 본 셈이겠다.

정하웅 교수님은 이미 많은 독자들이 잘 알고 있겠지만 “데이터 과학^{data science}”의 전문가로서 “구글 신은 모든 것을 알고 있다”라는 책을 공저했다. 재미있는 여담으로, 정 교수님은 이번 카오스 강연의 제목을 정할 때 고민을 많이 했는데, 필자가 약간 도움이 되었다. 구체적으로, 어느 날 필자는 강연 준비를 위한 사전 회의에서 정 교수님과 얘기를 나누게 되었다. 이때 정 교수님은 “구글 신”이라는 용어는 이미 많이 썼기 때문에 조금 더 신선한 제목을 찾고 싶어 했다. 그리고 그 제목은 “세상 모든 것을 설명하는 이론은 과연 가능한가?”라는 전체 주제에도 부합해야 했다.

이에 “모든 것의 이론^{theory of everything}”이라는 용어가 제안되었지만, 이 용어는 곧고에너지 물리학^{high-energy physics}에서 특별한 의미로 쓰이는 용어라 적합하지 않다는 반대 의견이 나왔다. 참고로, 고에너지 물리학에서 “모든 것의 이론”이란 중력과 양자역학을 통합하는 이론을 말한다. 그러한 이론을 정립하는 것은 고에너지 물리학의 최종적인 목표 중의 하나이다. 어쨌든, 다른 용어가 필요했다. 이때, 필자가 정 교수님에게 “모든 것” 다음에 “들”을 붙여서 “모든 것들의 이론”이 어떻겠냐고 제안을 했다. 데이터 과학은 많은 개체를 다루는 “다체 문제^{many-body problem}”의 일종이므로 “많다”라는 성질을 강조하자는 아이디어였다. 정 교수님은 이 아이디어를 즉각적으로 좋아하셨고 그렇게 해서 “모든 것들의 이론”이라는 제목이 탄생했다.

김민형 교수님의 강연 제목은 더 강렬했다. 사실 이 제목은 수학에서 자주 회자되는 질문 중의 하나라고 하는데, 필자도 예전에 들어본 적이 있었다. 그 질문은 다음과 같다.

“우주는 대수적인가, 기하학적인가?”
^{“Is the Universe algebraic or geometric?”}

대중 관객을 위해서 조금 더 쉬운 용어를 써야 한다는 의견이 있어서 제목은 최종적으로 다음과 같이 정해졌다.

“우주는 수인가, 모양인가?”
^{“Is the Universe a number or a shape?”}

김 교수님의 답은 “우주는 크게 보면 모양이고, 작게 보면 수이다”였다. 도대체 무슨 얘기일까? 이 답의 의미는 대강 다음과 같다. 우선, 큰 스케일에서 우주를 기술하는 고전역학의 세계에서는, 원리적으로 모든 입자들이 그리는 궤적을 뉴턴의 운동방정식을 통해서 계산할 수 있다. 이렇게 우주 안에 존재하는 모든 입자들이 그리는 궤적의 모양을 정확하게 결정할 수 있다면 기본적으로 우주를 다 알게 되는 것이다. 이것은 바로 “믿기 힘든 양자 Incredible Quantum [3]: 미분 방정식”에서 언급한 라플라스^Laplace가 그토록 절절하게 표현한 시계 장치 우주^{clockwork universe}의 관점이다. 반면에 작은 스케일에서 우주를 기술하는 양자역학의 세계에서는, 근본적인 양자 요동으로 인해서 입자가 그리는 궤적의 모양을 정확하게 결정하는 것이 아예 불가능하다. 이런 이유로 우주는 작게 보면 잘 정의된 모양을 갖지 않는다. 그래도 궁금증은 남는다. 모양이 아닌 것은 알겠는데, 왜 수일까? 조금 더 현학적으로 말해서, 양자역학은 왜 대수적일까? 이 질문에 대한 답은 이번 글의 주제인 양자역학을 바라보는 세 번째 관점인 연산자의 관점과 연결된다.

사실 연산자의 관점은 역사적으로 볼 때 가장 처음 발견된 양자역학적 관점이다. 이야기는 베르너 하이젠베르크^{Werner Karl Heisenberg, 1901-1976}로부터 시작된다. 하이젠베르크는 양자역학이 고전역학과 질적으로 다른데, 그 근본적인 이유가 우리가 측정하고 관찰할 수 있는 물리량, 예를 들어 입자의 위치와 운동량이 단순히 숫자가 아니라 행렬^matrix이기 때문이라고 생각했다. 그래서 하이젠베르크가 고안한 양자역학을 특별히 행렬역학^{matrix mechanics}이라고 부른다. 단도직입적으로 말해서 이러한 행렬이 연산자이다. 행렬을 가지고 물리량을 계산하려면 항상 모종의 대수적인 작업을 거쳐야 한다. 따라서 양자역학은 대수적이라는 명제가 나온다. 이 명제에 대해서 조금 더 깊숙하게 파보자.“믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 운동량은 기본적으로 미분연산자와 같다고 했다. 그런데, 위에서 하이젠베르크가 주장하는 바는 운동량을 포함해서 모든 관찰 가능한 물리량이 연산자, 특히 행렬로 기술되는 선형 연산자^{linear operator}라는 것이다. 필자가 갑자기 던진 이 말에 독자들이 당황하지 않았기를 바란다. 행렬은 바둑판과 같은 사각형 모양 격자의 각 칸에 숫자를 하나하나 채워 넣은 것인데, 이것이 왜 연산자인가? 이 질문에 답을 하기 위해서, 우선 파동 함수가 숫자의 사슬^chain로 표현될 수 있음을 알아야 한다.

“믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 임의의 파동 함수는 정상파들의 합으로 완벽하게 분해될 수 있다고 했다. 이것을 표현하는 공식을 다시 써 보자. \[\psi({\bf r})=\sum_n c_n \varphi_n({\bf r})\]이 공식을 자세히 음미해 보면, 임의의 파동 함수는 정상파들을 모두 안다는 가정 하에 각각의 정상파 앞에 붙어있는 계수를 알면 완벽하게 결정된다. 이런 의미에서 파동 함수는 숫자의 사슬이다.\[|\psi\rangle=\left(\begin{array}{c}c_1 \\c_2 \\c_3 \\\vdots\end{array}\right)\]여기서 파동 함수는 공간에 대한 함수가 아니라 숫자의 사슬로 표현되므로, 보통의 함수 \(\psi({\bf r})\)가 아니라 새로운 기호인 \(|\psi\rangle\)를 도입하였다. 전문적으로 이러한 기호를 사용하는 표기법을 브라-켓 표기법^{bra-ket notation}이라고 부른다. 브라-켓 표기법은 디랙 방정식으로 유명한 폴 디랙^{Paul Dirac}에 의해 개발되었다. 이 표기법은 굉장히 중요해서 이후에 계속 쓰게 될 것이다.

그런데, 숫자의 사슬을 수학에서는 벡터^vector라고 부른다. 다시 말해서, 이제 파동 함수는 공간에 대한 함수가 아니라 어떤 가상의 공간에 존재하는 벡터라고 볼 수 있다. 이 가상의 공간은 보통의 \(x\), \(y\), \(z\) 축으로 이루어진 3차원 공간이 아니라 각각의 정상파들이 하나하나 방향의 역할을 맡고 있는 무한 차원의 공간이다. 이 가공의 공간을 전문적으로 힐버트 공간^{Hilbert space}이라고 부른다.

브라-켓 표기법은 영어의 의미를 알면 굉장히 직관적으로 이해할 수 있다. 위 \(|\psi\rangle\)는 켓^ket이라고 불리는데, 켓에게는 천생연분의 짝이 있다. 그 짝의 이름은 바로 브라^bra이다. 브라와 켓이 서로 짝인 이유는 둘이 만나면 숫자 하나를 만들어 내기 때문이다. 브라는 \(\langle\psi|\)로 표기되고, 기본적으로 그것의 짝인 켓의 복소수 켤레^{complex conjugate}이다. 수학적으로는 다음과 같이 쓰인다.\[\langle\psi|=(c_1^*,c_2^*,c_3^*,\cdots)\]수학적인 전통에 따라서 켓은 세로로 긴 숫자의 사슬로 쓰고 브라는 가로로 긴 숫자의 사슬로 쓴다. 브라와 켓이 만나서 만들어 내는 숫자는 각 사슬의 첫번째 숫자 쌍부터 시작해서 같은 순서에 있는 숫자 쌍끼리 차례차례 곱해서 더한 합이다. 그런데 이것은 바로 다름 아닌 내적^{inner product}이다. 다른 말로 표현하면, 그것은 힐버트 공간 상의 두 벡터의 스칼라곱^{scalar product}이다.

구체적으로, 브라 \(\langle\psi|\)와 \(|\psi\rangle\) 사이의 내적을 수학적으로 표현하면 다음과 같다.\[\langle\psi| \psi\rangle=|c_1|^2+|c_2|^2+|c_3|^2+\cdots=\sum_i |c_i|^2\]혹시 예상한 독자가 있을지 모르겠으나, 위 내적의 값은 1이어야 한다. 그 이유는 이 값이 파동 함수 \(\psi\)의 절대값의 제곱을 모든 경우에 대해서 다 더한 것이기 때문이다. “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 파동 함수의 절대값의 제곱을 전 공간에 대해서 다 적분하면 1이 되어야 한다고 했다. 이는 물론 입자가 존재 가능한 모든 위치에 존재할 확률을 다 더하면 1이 되어야 하기 때문이다. 위에서는 파동 함수를 정상파들의 합으로 분해했다. 이때 \(|c_i|^2\)의 의미는 입자가 \(i\)번째 정상파에 존재할 확률이다. 따라서 그것들을 다 더하면 역시 1이어야 한다. 그리고 내적의 의미는 벡터의 길이이다. 따라서, 결론적으로 임의의 파동 함수는 힐버트 공간 상에 존재하는 길이가 1인 벡터이다. 서로 다른 파동 함수는 길이는 모두 1로 같지만 방향이 서로 다른 벡터들인 것이다.

이제 우리는 브라-켓 표기법의 의미를 이해할 수 있다. 브라와 켓이 만나면 발음 상 브라켓이 되는데, 이것과 같은 발음을 가진 단어로 bracket이 있다. 이 단어는 bra와 ket 사이에 c를 집어 넣어 연결시킨 것으로 문자 그대로 꺾어진 괄호 <>를 의미한다. 다시 말해서, 브라와 켓은 브라켓을 두 개로 쪼개어 만들어 진 것이다. 살짝 유치한 말장난이라는 느낌이 들기도 하지만, 어찌 보면 참 신선한 작명법이라는 생각이 든다. 필자가 생각하기에, 전 물리 영역에 걸쳐서 이 정도로 유머 감각이 들어간 이름은 없는 것 같다.

위 논의에서는 같은 파동 함수에서 나온 브라 \(\langle\psi|\)와 켓 \(|\psi\rangle\) 사이의 내적을 계산해 보았다. 그렇다면 서로 각각 다른 파동 함수에서 나온 브라 \(\langle\psi^\prime|\)와 켓 \(|\psi\rangle\) 사이의 내적을 취하면, 어떻게 될까? 물론 이 내적은 그 값이 일정하게 정해지지 않는다. 이때의 내적은 두 파동 함수가 서로 얼마나 비슷한가를 재는 양으로서 전문 용어로 “오버랩^overlap”이라고 불린다. 오버랩은 우리나라 말로 번역하면 “겹침”이라고 할 수 있을 텐데, 그것의 의미는 브라와 켓이 서로 같은 파동 함수에서 나왔다면 오버랩은 1이 되고 서로 전혀 관계가 없으면 0이 된다는 성질로부터 얻어진다. 여기서 두 파동 함수가 서로 전혀 관계가 없다는 것에 대해서 약간 더 자세하게 설명할 필요가 하다.

앞에서 주장하기를, 임의의 파동 함수는 힐버트 공간에 존재하는 길이가 1인 벡터로 생각할 수 있다고 했다. 그런데 곰곰이 생각해 보면, 이 주장은 “임의의 파동 함수는 정상파들의 합으로 완벽하게 분해할 수 있다”라는 명제와 완전히 같은 명제가 아니다. 사실 앞선 주장에서 필자는 독자들에게 자세하게 설명하지 않고 정상파들이 만족하는 성질 중의 하나를 은근슬쩍 사용했다. 그것은 바로 “정상파들은 서로 독립적이다”라는 성질이다. 여기서 “서로 독립적이다”라는 의미는 보통의 3차원 공간에서 각각 3 방향을 맡고 있는 \(x\), \(y\), \(z\) 축이 “서로 수직이다”라는 의미와 같다. 다시 말해서, 힐버트 공간에서 각각의 정상파는 하나하나 방향을 맡고 있는데, 그 방향이 서로 수직인 것이다. 방향이 서로 수직이라는 것은 하나의 주어진 정상파를 그것을 제외한 다른 모든 정상파들의 합으로 나타낼 수 없다는 것이다. 따라서 모든 정상파는 각각 완전히 독립적이다. 수학적으로 표현하면, 서로 다른 두 정상파 사이의 내적은 0이다.

“믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 “정상파들은 완전성을 지닌다”라고 했다. 그리고 위에서 “정상파들은 서로 수직이다”라고 했다. 마지막으로, 정상파도 파동 함수의 일종이므로 그것의 길이도 1이어야 한다. 정상파가 이러한 세 가지 성질을 동시에 가진다는 사실을 표현하기 위해서 다음과 같이 무시무시하게 들리는 문장이 만들어 진다.

“정상파들은 완전성을 지니고 서로 수직이며
정규적인 집합^{complete orthonormal set}을 이룬다”

여기서 정규적^normal이라는 용어는 길이가 1이라는 말을 어렵게 쓴 것이다. 무시무시하게 들리지만 위 문장은 각각의 정상파가 힐버트 공간에서 서로 수직인 방향을 하나하나 맡고 있다는 얘기를 어렵게 쓴 것에 불과하다.

아직 완벽하게 소화되지는 않았겠지만, 앞선 논의를 통해서 임의의 파동 함수는 힐버트 공간 상의 벡터로 표현될 수 있다는 사실을 알았다고 하자. 이제 이전 글 “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 열심히 얘기한 전파 인자^propagator가 힐버트 공간에서 어떻게 나타나는지 생각해 보려고 한다. 기억을 되살려 보면, 전파 인자가 하는 역할은 초기에 주어진 파동 함수가 시간이 흘러 다른 파동 함수로 어떻게 바뀌는가 알려주는 것이다. 힐버트 공간에서 보면, 이것은 초기에 주어진 벡터가 시간이 흘러 다른 벡터로 어떻게 바뀌는가 알려 주는 것이다. 다시 말하면, 전파 인자는 초기에 주어진 벡터를 시간의 함수로 회전시키는 역할을 한다.

“믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 전파 인자를 유도했던 과정을 기억해 보면, 가장 핵심적인 사실은 정상파가 각각 자기 고유의 진동수를 가지고 진동한다는 것이었다. 그리고 이것은 시간이 흐른 후의 파동 함수를 얻기 위해서, 각각의 정상파에 그것의 에너지와 시간의 곱을 위상각의 자리에 넣은 위상 인자를 곱하면 된다는 것을 의미했다. 따라서 전파 인자는 정상파들이 각 축을 형성하는 힐버트 공간에서 다음과 같이 매우 간단한 형태의 행렬로 써진다.

\(\hat { U } (t-t_{ 0 })=\left( \begin{array}{cccc} e^{ -iE_{ 1 }(t-t_{ 0 })/\hbar } & 0 & 0 & \cdots \\ 0 & e^{ -iE_{ 2 }(t-t_{ 0 })/\hbar } & 0 & \cdots \\ 0 & 0 & e^{ -iE_{ 3 }(t-t_{ 0 })/\hbar } & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{array} \right)\)

위 행렬은 초기 시각 \(t_0\)와 최종 시각 \(t\)를 연결하는 전파 인자를 나타낸다. 이렇게 행렬로 표현된 전파 인자를 쓰면, 초기 시각의 파동 함수를 나타내는 켓 \(|\psi(t_0)\rangle\)로부터 최종 시간의 파동 함수를 나타내는 켓 \(|\psi(t)\rangle\)를 얻는 공식은 다음과 같이 간단해 진다. \[|\psi(t)\rangle=\hat{U}(t-t_0)|\psi(t_0)\rangle\]참고로, “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서는 전파 인자를 행렬로 표현하지 않고 공간에 의존하는 일반적인 함수 \(U(x,x_0;t-t_0)\)로 표현했다. 그리고 이렇게 공간 변수로 표현된 전파 인자를 써서 파동 함수의 시간에 따른 진화를 기술하는 공식은 다음과 같았다. \[\psi(x,t)=\int^\infty_{-\infty} dx_0 U(x,x_0;t-t_0)\psi(x_0,t_0)\]자, 행렬로 표현된 방식이 훨씬 더 간단해 보이지 않는가? 그런데 놀랍게도 위에 있는 두 가지 표현 방식은 겉으로는 다르게 보일 지 모르지만 사실 정확히 같은 내용을 의미한다. 왜 그런지에 대해서 아래 자세하게 설명을 할 예정이니 인내심을 가지고 참아 주기를 부탁한다.

전파 인자는 여러 연산자 중의 하나이다. 일반적으로 연산자는 힐버트 공간 상에 존재하는 하나의 벡터를 다른 벡터로 변화시키는 수학적인 작업을 통칭한다. 그리고, 이러한 수학적인 작업은 언제나 행렬로 표현될 수 있다.

\(\hat { M } =\left( \begin{array}{cccc} M_{ 11 } & M_{ 12 } & M_{ 13 } & \cdots \\ M_{ 21 } & M_{ 22 } & M_{ 23 } & \cdots \\ M_{ 31 } & M_{ 32 } & M_{ 33 } & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{array} \right)\)

구체적으로, \(|\psi\rangle\)로 표시되는 어떤 파동 함수에 \(\hat{M}\)이라는 연산자를 작용하는 것은 행렬과 벡터의 곱으로 이해될 수 있다.

\(\hat{M}|\psi\rangle=\left(\begin{array}{cccc}M_{11} & M_{12} & M_{13} & \cdots \\M_{21} & M_{22} & M_{23} & \cdots \\M_{31} & M_{32} & M_{33} & \cdots \\\vdots & \vdots & \vdots & \ddots\end{array}\right)\left(\begin{array}{c}c_{1} \\c_{2} \\c_{3} \\\vdots\end{array}\right)=\left(\begin{array}{c}M_{11} c_1 + M_{12} c_2 + M_{13} c_3 + \cdots \\M_{21} c_1 + M_{22} c_2 + M_{23} c_3 + \cdots \\M_{31} c_1 + M_{32} c_2 + M_{33} c_3 + \cdots \\\vdots\end{array}\right)\)

물론 이 곱은 연산자가 작용한 후에 얻어진 새로운 파동 함수를 의미한다.

이제 전파 인자 외에 다른 예를 생각해 보자. 앞에서 운동량은 단순히 숫자가 아니라 공간에 대한 미분연산자라고 했다.

\({\bf p}=-i \hbar \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\)

이 운동량 연산자를 어느 한 파동 함수에 작용시킨다는 의미는 기본적으로 그 파동 함수를 공간에 대해서 미분한다는 의미이다. 미분 이후에 얻어지는 함수도 또 다른 새로운 파동 함수로 생각할 수 있는데 이 새로운 파동 함수도 다시 정상파들의 합으로 분해할 수 있다. 따라서 운동량 연산자도 힐버트 공간 상의 한 벡터에서 다른 벡터로 변환시키는 연산자 중의 하나인 것이다. 이때 물론 벡터의 길이는 변한다. 운동량 연산자를 나타내는 행렬의 구체적인 형태는 일반적으로 매우 복잡하므로 여기서 쓰지는 않기로 한다. 비슷하게, 공간 상의 위치를 나타내는 평범한 벡터 \({\bf r}=(x,y,z)\)도 힐버트 공간에서 보면 매우 복잡한 연산자이다. 그 이유는 어떤 파동 함수에 을 곱하면 전혀 새로운 파동 함수가 얻어지는데, 이 새로운 파동 함수를 정상파들의 합으로 분해하면 운동량 연산자와 비슷하게 일반적으로 매우 복잡한 형태가 되기 때문이다.

하이젠베르크는 모든 “관찰 가능한 물리량^observable”은 연산자로 표현된다고 생각했다. 그런데, 가만히 생각해 보면 우리가 관찰할 수 있는 (거의) 모든 물리량은 입자의 위치와 운동량의 적절한 조합으로 이해될 수 있다. 따라서, 위치와 운동량을 나타내는 연산자를 알면 양자역학을 (거의) 다 알게 된 것이다. 다행히도, 우리는 답을 이미 기본적으로 알고 있다. 그것은 바로 위치 연산자는 파동 함수에 위치 변수를 그냥 곱하는 것이고, 운동량 연산자는 파동 함수를 공간에 대해서 미분하고 상수인 \(-i\hbar\)를 곱하는 것이다. 사실 이 답을 알고 있으면 하이젠베르크의 행렬역학을 기본적으로 (거의) 다 알고 있는 것이다. 문제는 앞서 말했듯이 정상파들이 각 축을 구성하는 힐버트 공간에서는 그것들의 행렬이 일반적으로 매우 복잡한 형태를 띤다는 사실이다.

여기서 행렬역학의 관점에서 양자역학을 바라 볼 때 매우 중요한 사실 하나가 그 모습을 드러낸다. 그것은 바로 임의의 파동 함수를 꼭 정상파들이 아닌 다른 기본 파동들의 합으로도 분해할 수 있다는 사실이다. 일종의 자유도^{degree of freedom}가 있는 것이다.정상파처럼 임의의 파동 함수를 분해할 수 있는 기본 파동들을 전문적으로 “기저^basis”라고 부른다. 이러한 기저들은 정상파와 비슷하게 완전성을 지니고 서로 수직이며 정규적인 집합을 이룬다. 이 조건을 만족하는 한, 기저들의 구체적인 형태는 마음대로 정할 수 있다. 비유적으로 말하면, 다른 기저를 선택한다는 것은 힐버트 공간을 구획하는 축^axis을 다른 축으로 바꾸는 것을 의미한다. 구체적으로 3차원 공간의 예를 들면, \(x\), \(y\), \(z\) 축 대신에 회전된 축인 \(x^\prime\), \(y^\prime\), \(z^\prime\) 축을 사용할 수 있다는 것이다.

사실은 엄밀하게 말해서, 파동 함수를 브라나 켓, 다시 말해서 긴 숫자의 사슬로 나타낼 때, 우리는 어떠한 기저로 파동 함수를 분해했는지 명확하게 표시해 주어야 한다. 아니면 이 숫자들이 어떤 기저를 잡았을 때 나온 것인지 알 수 없기 때문이다. 그렇다면 어떻게 기저를 표시할 수 있을까? 기저를 표시하는 문제는 생각보다 우아하게 해결된다. 예를 들어서, 정상파도 당연히 파동 함수의 일종이므로 그것도 켓으로 쓸 수 있어야 한다. 다시 말해서, \(n\)번째 정상파를 기술하는 파동 함수를 \(\varphi_n({\bf r})\)라고 할 때, 그것의 켓을 \(|\varphi_n\rangle\)이라고 쓸 수 있다. 그렇다면, 임의의 파동 함수를 나타내는 켓 \(|\psi\rangle\)는 다음과 같이 분해될 수 있다.\[|\psi\rangle=\sum_n c_n |\varphi_n\rangle\]여기서 각각의 정상파 앞에 붙는 계수 \(c_n\)은 정상파들이 서로 수직하고 정규적^orthonormal이라는 사실을 이용하면 결정할 수 있다. 무슨 소리인가?

앞에서 정상파는 힐버트 공간에서 각각 수직인 방향을 하나씩 담당한다고 했다. 따라서 서로 다른 두 정상파 사이의 내적은 0이다. 내적이 브라와 켓을 곱하면 얻어지는 숫자라는 것을 기억할 때, 서로 다른 두 정상파들이 수직이라는 사실은 다음과 같은 수식으로 표현된다.\[\langle \varphi_m | \varphi_n \rangle = \delta_{mn}\]여기서 우변에 있는 \(\delta_{mn}\)는 크로네커 델타^{Kronecker delta}라고 불리는 기호인데, 아주 거창한 것은 아니고, \(m\)과 \(n\)이 같으면 1이고, 다르면 0을 준다는 것을 나타내는 기호이다. 이제 앞에서 \(|\psi\rangle\)를 정상파들의 합으로 분해하는 수식의 양변에 특정 정상파의 브라, 예를 들어 \(\langle\varphi_m|\)을 곱해 보자.\[\langle \varphi_m | \psi \rangle = \sum_n c_n \langle \varphi_m |\varphi_n \rangle = c_m\]따라서, 앞에서 예고했듯이 우리는 정상파 앞에 붙는 계수를 결정할 수 있다. 즉, \(n\)번째 계수는 주어진 파동 함수와 \(n\)번째 정상파의 내적이다.

이 즈음에서, 독자들의 정신 세계를 뒤흔들어 놓을 만한 수학적 유희를 하나 즐겨보자. 앞서 얻은 결론에 따라서, 주어진 파동 함수를 정상파들의 합으로 분해하되, 정상파 앞에 붙은 계수를 다시 주어진 파동 함수와 정상파의 내적으로 써 보자. 약간 돌고 도는 순환 논리 같지만, 그렇게 해 보면 다음과 같은 수식에 다다른다.\[|\psi\rangle=\sum_n |\varphi_n\rangle \langle \varphi_n |\psi\rangle=\left( \sum_n |\varphi_n \rangle \langle \varphi_n | \right) |\psi\rangle\]위에서 좌변과 우변은 항상 같아야 하므로, 다음의 항등식이 만족된다.\[\sum_n |\varphi_n\rangle\langle \varphi_n |=1\]여기서 중요한 사실은 정상파를 나타내는 브라와 켓을 브라-켓 순서로 곱하지 않고 켓-브라 순서로 곱하고 모든 가능한 정상파에 대해서 다 더하면 항상 1이라는 것이다. 이 공식은 앞으로 꽤 자주 쓰게 될 공식으로, 다름 아니라 정상파가 완전성을 지닌다는 것을 의미하는 수학적 표현이다. 이 공식의 이름은 “완전성 관계식^{completeness relation}”이다.

지금까지 포기하지 않고 잘 따라온 독자가 있다면, 진심으로 경의를 표하고 싶다. 파동 함수를 힐버트 공간이라는 가공의 공간 속에 존재하는 하나의 벡터라고 해석할 수 있다는 사실은 아마도 양자역학에 있어서 가장 추상적인 내용 중의 하나일 것이다. 사실, 시공간의 함수로 잘 쓸 수 있는 파동 함수를 굳이 이렇게까지 복잡하게 생각할 필요가 있느냐고 질문할 수 있다. 건전한 정신 상태를 가진 사람이라면 충분히 물어볼 수 있는 정상적인 질문이다.

여러 종류의 답이 있을 수 있겠으나, 가장 명료한 답은 시공간의 함수로 아예 쓸 수 없는 파동 함수가 있기 때문이다. 그것은 바로 스핀^spin의 상태를 나타내는 파동 함수이다. 스핀의 상태는 입자의 위치와 운동량으로 기술되지 않는다. 스핀은 스피너^spinor 공간이라고 불리는 “정말로” 가공의 힐버트 공간에 존재한다. 지금까지 얘기한 힐버트 공간도 가공의 공간인데, 스피너 공간이야말로 정말로 가공이라니… 스핀에 관한 자세한 얘기는 다음에 이어질 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 하기로 하고 다시 본론으로 돌아가자.

본론으로 돌아가서, 정상파가 아닌 다른 기저로 파동 함수를 분해하면 어떤 일이 벌어지는지 생각해 보자. 특히, 위치 연산자의 고유함수를 기저로 사용해서 파동 함수를 분해하면 어떻게 되는지 생각해 보자. (참고로, 정상파는 해밀토니안의 고유함수이다.) 우선, 위치 연산자의 고유함수란 도대체 무엇인가? 위치 연산자는 위치를 재는 연산자이다. 공간에 퍼져 있는 일반적인 파동 함수의 위치는 물론 하나의 숫자로 딱 떨어지지 않는다. 위치가 하나의 숫자로 딱 떨어지는 파동 함수는 아주 특별한 함수로서, 주어진 위치 주변의 굉장히 작은 범위 안에 국소적으로 몰려있는 파동을 기술한다. 거칠게 말해서, 그러한 파동 함수는 공간의 한 점에서 발산하지만 전 공간에 대해서 적분하면 그 값이 1로 남는 이상한 함수이다. 그 파동 함수의 이름은 “디랙 델타 함수^{Dirac delta function}”이다.

디랙 델타 함수도 보통의 정상파와 마찬가지로 완전성을 지니며 서로 수직이고 정규적인 기저를 구성한다. 편의상, 1차원 상에서 \(x\)라는 위치에 입자가 정확히 위치하는 상황을 하는 디랙 델타 함수를 나타내는 켓을 \(|x\rangle\)이라고 표시할 때, 앞에서 설명한 완전성 관계식을 적용하면 주어진 파동 함수를 다음과 같이 디랙 델타 함수들의 합으로 분해될 수 있다.\[|\psi\rangle= \sum_x |x\rangle\langle x|\psi\rangle=\sum_x |x\rangle \psi(x)\]이것이 의미하는 바는, 주어진 파동 함수를 디랙 델타 함수들의 합으로 분해할 때 그 계수는 다름 아니라 공간의 함수로 표현된 파동 함수라는 사실이다!

이제, 재미가 들렸으니, 위치 연산자가 아닌 운동량 연산자의 고유함수로 임의의 파동 함수를 분해하면 어떤 일이 벌어지는지 생각해 보자. 운동량 연산자의 고유함수는 무엇인가? 그것은 바로 우리가 좋아하는 평면파^{plane wave}이다. 위에서와 비슷하게 평면파에 대해서 완전성 관계식을 쓰면 다음과 같다.\[|\psi\rangle= \sum_p |p\rangle\langle p|\psi\rangle=\sum_p |p\rangle \tilde{\psi}(p)\]여기서 \(\tilde{\psi}(p)\)는 주어진 파동 함수와 운동량 \(p\)를 가지는 평면파 사이의 내적이다. 물론, \(|\tilde{\psi}(p)|^2\)의 물리적인 의미는 주어진 파동 함수가 운동량 \(p\)를 가질 확률이다.

이제, 위 공식에 디랙 델타 함수의 완전성 관계식을 다시 쓰면 재미있는 일이 벌어진다.

\(|\psi\rangle= \sum_x |x\rangle\langle x| \sum_p |p\rangle \tilde{\psi}(p)=\sum_x |x\rangle \sum_p \langle x|p\rangle \tilde{\psi}(p)=\sum_x |x\rangle \sum_p e^{i px/\hbar} \tilde{\psi}(p)\)

위에서 \(\langle x | p \rangle\)는 평면파와 디랙 델타 함수 사이의 내적으로, 평면파를 공간 변수로 나타냈을 때의 파동 함수인 \(e^{i px/\hbar}\)와 같다. 이 공식과 위에서 파동 함수를 디랙 델타 함수들의 합으로 분해한 공식을 비교하면 다음과 같은 결론을 얻는다.\[\psi(x)=\sum_p e^{i px/\hbar} \tilde{\psi}(p)\]이 결론의 의미는 무엇인가? 이 결론이 의미하는 바는 위치 연산자의 고유함수로 분해된 파동 함수와 운동량 연산자의 고유함수로 분해된 파동 함수는 서로 푸리에 변환^{Fourier transform}에 의해 연결된다는 사실이다.

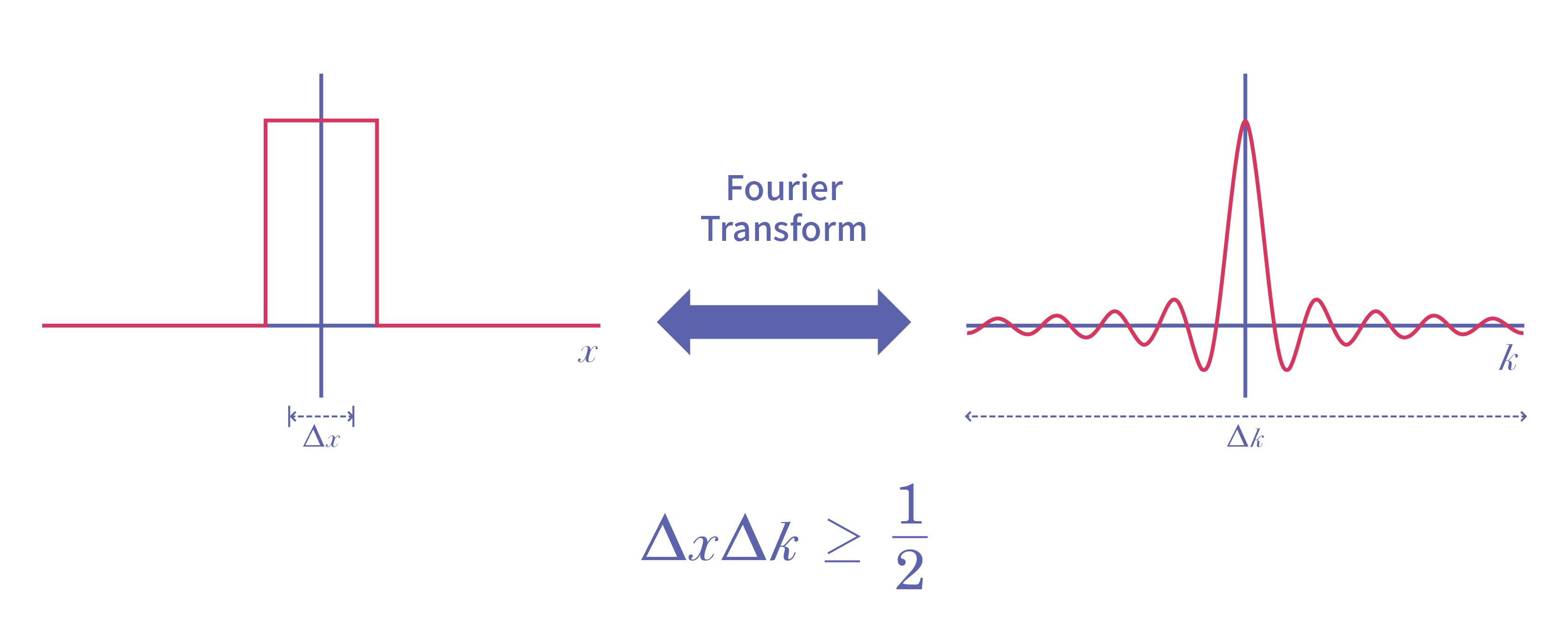
사실, 위에서 우리는 인지하지 못하는 사이에 양자역학에서 가장 유명한 원리 중의 하나를 유도했다. 그 원리는 바로 하이젠베르크의 “불확정성 원리^{uncertainty principle}”이다. 구체적으로, 불확정성 원리는 입자의 위치와 운동량을 동시에 확정하는 것이 불가능하다는 원리이다. 그런데, 이 원리를 수학적으로 구체화하면 “위치와 운동량은 서로 푸리에 변환에 의해 연결된다”로 표현된다.

푸리에 변환에 대해서는 “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 약간 논의를 했다. 예를 들어, 푸리에 변환은 시간에 따라 변하는 음악과 주파수 별로 분해된 음의 세기 사이의 관계를 말해 준다고 했다. 양자역학적으로, 푸리에 변환은 위치에 따라 변하는 파동 함수와 그 파동 함수를 평면파들의 합으로 분해했을 때 각 평면파의 세기를 말해 준다. 이제, 이렇게 푸리에 변환에 의해 연결되는 위치와 운동량 사이에 불확정성이 있다는 사실을 이해하기 위해서 두 극한을 생각해 보자.

첫 번째 극한으로, 모든 공간에 가장 널리 골고루 퍼져있는 파동 함수를 생각해 보자. 그러한 파동 함수는 바로 평면파를 기술하는 파동 함수이다. 평면파의 운동량은 잘 정의된 하나의 값을 가진다. 반면에 평면파는 모든 공간에 골고루 퍼져있으므로 그것의 위치는 완전히 불확정적이다. 두 번째 극한으로, 위치 연산자의 고유함수인 디랙 델타 함수를 생각해 보자. 이 경우에는 위치가 잘 정의된다. 하지만 디랙 델타 함수의 푸리에 변환은 운동량의 관점에서 보면 완전히 퍼진 함수가 되어, 그 운동량이 완전히 불확정적이게 된다. 이 두 극한의 예로부터 우리는 모종의 상보적인 관계^{complementary relation}가 있음을 느낄 수 있다.

여기서 푸리에 변환에 관한 엄밀한 수학적인 논의를 하지는 못 할 것이다. 다만, 필자는 불확정성 원리는 푸리에 변환이 가지는 하나의 성질이라는 사실을 강조하고 싶다. 다시 말해서, 푸리에 변환의 성질로부터 다음을 증명할 수 있다. 임의의 파동 함수는 그것이 어떠한 형태를 가질지라도 각각 위치와 운동량의 함수로 퍼져있는 정도 사이에 아래와 같은 불확정성 원리가 존재한다.\[\Delta x \Delta p \geq \frac{\hbar}{2}\]여기서 \(\Delta x\)는 파동 함수를 위치의 함수로 나타냈을 때 그것이 퍼진 정도이고 \(\Delta p\)는 파동 함수를 운동량의 함수로 나타냈을 때 그것이 퍼진 정도이다.

잠깐 멈추어 위에서 우리가 무엇을 이루었는지 곱씹어 보자. 위에서 우리는 파동 함수를 위치 연산자의 고유함수들의 합으로 분해하는 것과 운동량 연산자의 고유함수들의 합으로 분해하는 것이 서로 같다는 조건을 써서 불확정성 원리를 유도했다. 그런데 곰곰이 생각해 보면, 파동 함수를 임의의 기저를 써서 표현할 수 있다는 사실은 양자역학 자체를 기저의 선택에 상관없이 기술할 수 있어야 한다는 것을 의미한다. 다시 말해서, 파동함수를 어떻게 표현하느냐에 상관없이 바뀌지 않는 그 무엇이 있어야 한다는 것을 의미한다. 보통의 경우에는 파동 함수를 공간 변수에 의존하는 함수로 생각하는 것이 편리하겠지만, 꼭 그럴 필요가 없는 것이다.

그렇다면, 기저를 무엇으로 잡든지 간에 바뀌지 않는 연산자 본연의 성질은 무엇일까? 하이젠베르크는 그 본연의 성질이 연산자들 사이의 교환 관계^{commutation relation}라고 생각했다. 구제적인 예를 들어서, 위치 연산자인 \(x\)와 그 방향의 운동량 연산자인 \(p_x\) 사이의 교환 관계는 다음과 같다.\[[x, p_x]=x p_x -p_x x =i \hbar\]잘 생각해 보면, 이 공식은 위에서 언급한 하이젠베르크의 불확정성 원리를 연산자 사이의 교환 관계로 다시 표현한 것에 불과하다. 물론, 이 공식은 \(p_x=-i \hbar (\partial/\partial x)\)라는 사실을 이용하면 어렵지 않게 보일 수 있다. 다시 말해서, 위 공식을 임의의 함수 \(f(x)\)에 작용한다고 하자.\[[x, p_x]f(x)=x(-i \hbar) \frac{\partial f(x)}{\partial x} +i \hbar \frac{\partial(xf(x))}{\partial x} =i \hbar f(x)\]위 공식은 임의의 함수에 대해서 항상 만족하므로 짧게 줄여서 \([x,p_x]=i \hbar\)로 쓸 수 있다. 이 공식의 유도도 중요하지만, 사실 정말 중요한 것은 이 교환 관계가 어떠한 기저를 잡더라도 절대로 변할 수 없다는 사실이다.

참고로, \([A,B]=AB-BA\)를 연산자 \(A\)와 \(B\) 사이의 “교환자^commutator”라고 부른다. 연산자가 행렬로 표시한다는 입장에서 보면 위 교환자의 값이 반드시 0이 되지 않는 사실은 자연스럽게 이해될 수 있다. 그것은 왜냐하면 일반적인 두 개의 행렬 \(A\)와 \(B\) 사이의 곱은 곱하는 순서에 따라서 그 결과가 달라지기 때문이다. 하이젠베르크는 이렇게 연산자들이 “비교환적 대수^{noncommutative algebra}” 관계를 만족한다는 것이 양자역학의 핵심이라고 생각했다. 자, 이제 슬슬 본 글의 앞부분에서 언급한 양자역학은 대수적이라는 명제를 이해할 수 있는가?

여기서, 중요한 질문 하나가 대두된다. 연산자들이 기저에 상관없이 기술된다면, 슈뢰딩거 방정식도 기저에 상관없이 적혀야 하지 않을까? 다시 말해서, 하이젠베르크의 생각에 따르면 슈뢰딩거 방정식도 어떤 종류의 교환 관계로 적혀야 하지 않을까? 아름답게도, 답은 “그렇다”이다. 슈뢰딩거 방정식을 기저에 상관없는 연산자들 사이의 교환 관계로 적은 것을 “하이젠베르크 방정식^{Heisenberg equation}”이라고 부르고, 수학적으로는 다음과 같이 적힌다.\[\frac{d}{dt}\hat{A}=\frac{i}{\hbar}[\hat{H},\hat{A}]\]여기서 \(\hat{A}\)는 임의의 연산자이고 \(\hat{H}\)는 해밀토니안^Hamiltonian을 나타내는 연산자이다. 사실은 엄밀히 말해서 위에 나온 \(\hat{A}\)와 \(\hat{H}\)는 지금까지 얘기한 보통의 연산자가 아니라 하이젠베르크 연산자^{Heisenberg operator}라고 불리는 연산자이다. 자, 이제 이 하이젠베르크 방정식을 어떻게 유도할 수 있는지, 그리고 하이젠베르크 연산자는 도대체 무엇인지 얘기하고자 한다.

하이젠베르크 방정식을 유도하기 위해서, 전파 인자가 행렬역학에서 어떻게 나타나는가를 다시 기억해 보자. 앞에서 초기 상태를 나타내는 켓에 전파 인자 행렬을 곱하면 최종 상태를 나타내는 켓을 얻을 수 있다고 했다.\[|\psi(t)\rangle=\hat{U}(t-t_0)|\psi(t_0)\rangle\]편의상 위 공식을 “전파 인자 행렬 공식”이라고 부르기로 하자.

우선, 이 전파 인자 행렬 공식이 이전 글 “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 공간 변수로 나타낸 공식과 같다는 것을 증명하고 시작하자. 증명은 예상 외로 간단하다. 위 공식의 양변에 디랙 델타 함수의 브라 \(\langle x|\)를 작용한다.\[\langle x|\psi(t)\rangle=\psi(x,t)=\langle x|\hat{U}(t-t_0)|\psi(t_0)\rangle\]이제 \(\hat{U}(t-t_0)\)와 \(|\psi(t_0)\rangle\)의 사이에 완전성 관계식 하나를 삽입한다.\[\psi(x,t) = \sum_{x_0}\langle x|\hat{U}(t-t_0)|x_0\rangle\langle x_0|\psi(t_0)\rangle= \sum_{x_0}\langle x|\hat{U}(t-t_0)|x_0\rangle \psi(x_0,t_0)\]여기서 가변수 \(x_0\)에 대한 합은 기본적으로 적분으로 바꿀 수 있으므로 위 공식이 바로 우리가 찾던 전파 인자 공식이다. 참고로, 공간 변수의 함수로 표현된 전파 인자는 행렬로 표현된 전파 인자와 다음과 같이 연결된다.\[U(x,x_0;t-t_0)=\langle x|\hat{U}(t-t_0)|x_0\rangle\]이제 전파 인자가 어떤 방정식을 만족하는지 생각해 보자. 전파 인자 행렬 공식의 양변에 시간에 대한 미분 연산자를 작용하면 다음과 같다.

\(i \hbar \frac{d}{dt} |\psi(t)\rangle= i \hbar \frac{d}{dt} \hat{U}(t-t_0)|\psi(t_0)\rangle \)

그런데, 이 공식은 다름 아닌 슈뢰딩거 방정식과 같아야 한다.

\(i \hbar \frac{d}{dt} |\psi(t)\rangle = H|\psi(t)\rangle = H\hat{U}(t-t_0)|\psi(t_0)\rangle\)

위 두 방정식은 임의의 초기 파동 함수에 대해서 항상 성립하므로, 전파 인자는 아래와 같은 방정식을 만족해야 한다.\[i \hbar \frac{d}{dt} \hat{U}(t-t_0)=H\hat{U}(t-t_0)\]여기서 필자가 강조하고 싶은 것은 위 방정식이 새로운 것이 아니라 슈뢰딩거 방정식을 다른 방식으로 쓴 것뿐이라는 사실이다. 위 방정식을 “전파 인자 방정식”이라고 부르도록 하자.

하이젠베르크 방정식을 유도하기 위해서 마지막으로 한 가지 단계가 더 남았다. 파동 함수를 브라-켓 표기법으로 표현할 때, 우리가 관찰 가능한 어떤 물리량을 잰다는 것은 어떻게 표현될까? 이전 글에서 파동 함수가 위치 변수의 함수로 주어지면 \(|\psi(x,t)|^2\)이 입자가 주어진 시각 \(t\)에 위치 \(x\)에 존재할 확률이라고 했다. 이때 우리가 입자의 위치를 재고 싶다면 \(x\)의 평균값을 구하면 될 것이다. 수학적으로 말해서 \(x\)의 평균값은 다음과 같이 주어진다.

\(\langle x(t) \rangle = \int dx \; x |\psi(x,t)|^2\)

더 나아가 만약 물리량이 공간 변수에 복잡하게 의존하는 함수, 예를 들어 \(F(x)\)로 주어진다면 그것의 평균값은 다음과 같이 주어질 것이다.

\(\langle F(t) \rangle = \int dx F(x) |\psi(x,t)|^2\)

그런데, 우리가 관심있는 물리량이 공간 변수에 의존하지 않고 운동량에 의존한다면 어떻게 계산할 수 있을까?

이 문제를 해결하기 위한 실마리는 파동 함수를 위치 변수로 표현하지 말고 운동량 변수로 표현하면 될 것이라는 아이디어에서 얻어진다. 앞에서 위치 변수로 표현된 파동 함수를 푸리에 변환하면 주어진 운동량을 가질 확률, 즉 \(|\tilde{\psi}(p,t)|^2\)을 계산할 수 있다고 했다. 이 상황에서 우리가 입자의 운동량을 재고 싶다면 \(p\)의 평균값을 구하면 될 것이다.

\(\langle p(t) \rangle = \int dp \; p |\tilde{\psi}(p,t)|^2\)

물론 우리가 관심있는 물리량이 운동량의 복잡한 함수 \(G(p)\)로 주어진다면 그것의 평균값은 다음과 같이 주어질 것이다.

\(\langle G(t) \rangle = \int dp G(p) |\tilde{\psi}(p,t)|^2\)

지금까지는 좋았다. 이제, 더욱 더 일반적인 상황을 생각해 보자. 우리가 관심있는 물리량이 위치와 운동량 모두에 의존한다면 어떻게 계산해야 할까? 답부터 먼저 제시하겠다. 우리가 관심있는 물리량을 표현하는 연산자를 \(A\)라고 할 때, \(A\)의 평균값은 다음과 같이 계산된다.\[\langle A(t) \rangle = \langle \psi(t) | A | \psi(t) \rangle\]쉽게 말해서, \(A\)의 평균값은 \(A\)를 브라와 켓 사이에 집어 넣고 내적을 취하는 것이다. 여기서는 논의의 편의상 \(A\) 자체는 명시적인 시간 의존성이 없다고 가정하였다.

이제, 전파 인자 행렬 공식을 사용해서 \(A\)의 평균값을 계산하는 공식을 다시 쓰면 다음과 같다.\[\langle A(t) \rangle = \langle \psi(t) | A | \psi(t) \rangle =\langle \psi(t_0) | \hat{U}^\dagger(t-t_0) A \hat{U}(t-t_0) | \psi(t_0) \rangle\]위에서 \(\hat{U}^\dagger\)의 의미는 \(\hat{U}\)의 모든 원소를 복소수 켤레로 변환하고 행렬의 대각선 상에 놓인 원자들의 위치를 서로 바꾸어 얻어지는 새로운 행렬이다. 이렇게 하는 이유는 브라가 켓의 복소수 켤레이고 세로로 길게 나열된 숫자의 사슬을 가로로 길게 나열된 숫자의 사슬로 바꾸어 얻어지기 때문이다. 즉, 브라를 위한 전파 인자 행렬 공식은 다음과 같이 쓰인다.\[\langle \psi(t) |=\langle \psi(t_0) | \hat{U}^\dagger(t-t_0)\]참고로 \(\hat{U}^\dagger\)는 \(\hat{U}\)의 “에르미트 켤레^{Hermitian conjugate}”라고 불린다.

그런데, 위 공식의 의미를 곰곰이 생각해 보면, 이제 우리에게 더이상 파동 함수가 필요 없다는 사실을 깨달을 수 있다. 왜냐하면 우리에게 필요한 것은 연산자 \(A\)의 시간에 다른 변화인데, 그것은 다음과 같은 연산자를 새롭게 정의하면 되기 때문이다.\[\hat{A}(t)= \hat{U}^\dagger(t-t_0) A \hat{U}(t-t_0)\]이 새로운 연산자를 초기 파동 함수 \(\psi(t_0)\)에 작용하면 되는데, 이 파동 함수는 문자 그대로 초기 조건에 불과하다. 다시 말해서, \(\psi(t_0)\)는 시간에 따라서 변화하지 않는다. 이제부터 위에서 새롭게 정의된 연산자를 “하이젠베르크 연산자”라고 부르자.

이제, 하이젠베르크 연산자가 어떠한 방정식을 만족하는지 알아보자. 그러기 위해서 시간에 대한 미분 연산자를 위 공식의 양변에 작용하면 다음과 같은 공식이 얻어진다.\[i\hbar\frac{d}{dt} \hat{A}(t)= \left[ i\hbar\frac{d}{dt}\hat{U}^\dagger(t-t_0)\right] A \hat{U}(t-t_0)+\hat{U}^\dagger(t-t_0) A \left[ i \hbar \frac{d}{dt} \hat{U}(t-t_0) \right]\]여기에 앞에서 유도한 전파 인자 방정식을 사용하면 아래와 같은 공식을 얻을 수 있다.\[i\hbar\frac{d}{dt} \hat{A}(t)= -\hat{U}^\dagger(t-t_0) H A \hat{U}(t-t_0)+\hat{U}^\dagger(t-t_0) A H \hat{U}(t-t_0)\]위에서 해밀토니안 연산자의 에르미트 켤레는 자기 자신과 같다는 성질을 썼다. 그리고 에르미트 켤레에 관한 아래의 성질을 썼다.\[(AB)^\dagger=B^\dagger A^\dagger\]즉, 전파 인자의 에르미트 켤레는 아래 방정식을 만족한다.\[-i \hbar\frac{d}{dt}\hat{U}^\dagger(t-t_0)=\hat{U}^\dagger(t-t_0)H\]이제 전파 인자의 중요한 수학적 성질 하나를 사용하려고 한다. 그것은 바로 전파 인자는 자기 자신과 자신의 에르미트 켤레를 곱하면 1이라는 성질이다.\[\hat{U}(t-t_0)\hat{U}^\dagger(t-t_0)=1\]이것의 물리적인 의미는 대략 다음과 같다. 전파 인자는 초기 시각에서 최종 시각으로 각이 흘러갈 때 파동 함수가 어떻게 변하는가를 알려 준다. 이것의 복소수 켤레는 시간이 거꾸로 흐르는 상황을 기술한다. 따라서 전파 인자와 그것의 복소수 켤레의 곱은 시간이 초기 시각에서 최종 시각으로 흐른 후에 다시 시간이 거꾸로 흘러서 원래로 돌아가는 것이다. 다시 원래로 돌아왔으므로 아무 것도 변한 것이 없고, 따라서 전체적으로 생긴 변화는 아무 것도 없게 된다. 그것은 파동 함수에 1을 곱한 것과 같다.

이제, \(\hat{A}(t)\)를 시간에 대해서 미분했을 때 얻어지는 공식 중에서 \(H\)와 \(A\) 사이, 그리고 \(A\)와 \(H\) 사이, 각각 두 군데에 전파 인자와 그것의 에르미트 켤레의 곱을 삽입해 보자.\[i \hbar\frac{d}{dt} \hat{A}(t)= -\hat{U}^\dagger(t-t_0) H \hat{U}(t-t_0)\hat{U}^\dagger(t-t_0) A \hat{U}(t-t_0)+\hat{U}^\dagger(t-t_0) A\hat{U}(t-t_0)\hat{U}^\dagger(t-t_0) H \hat{U}(t-t_0)\]그리고 \(A\)에 해당하는 하이젠베르크 연산자를 \(\hat{A}(t)= \hat{U}^\dagger(t-t_0) A \hat{U}(t-t_0)\)와 같이 정의하듯이 해밀토니안 연산자 \(H\)에 해당하는 하이젠베르크 연산자를 다음과 같이 정의해 보자.\[\hat{H}(t)= \hat{U}^\dagger(t-t_0) H \hat{U}(t-t_0)\]그렇게 하면 앞선 \(\hat{A}(t)\)를 시간에 대해서 미분했을 때 얻어지는 공식은 다음과 같이 간단하게 정리된다.\[i \hbar \frac{d}{dt}\hat{A}(t)= -[\hat{H}(t),\hat{A}(t)]\]이것은 다름 아닌 앞에서 언급한 하이젠베르크 방정식이다!

자, 드디어 우리는 하이젠베르크 방정식을 슈뢰딩거 방정식으로부터 유도하는 데에 성공했다. 다시 말해서, 연산자의 관점이 왜 파동 함수의 관점과 같은지 알게 되었다. “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”의 결론과 비슷하게 연산자의 관점에서 양자역학을 바라 보면 파동 함수가 필요 없다. 가만히 생각해보면 파동 함수는 실제로 잴 수 있는 물리량이 아니다. 물론 전파 인자도 실제로 잴 수 없기는 마찬가지다. 하이젠베르크가 행렬역학을 고안했을 때, 그를 이끌었던 원칙은 실제로 관찰 가능한 물리량으로만 양자역학을 건설해야 한다는 것이었다.

하이젠베르크는, 원자 안에서 입자가 가질 수 있는 궤도가 양자화된다는 보어의 이론은 궁극적인 양자역학의 이론이 될 수 없다고 생각했다. 그 이유는 입자의 궤도가 정확하게 정의되지 않을 뿐만 아니라 아예 원리적으로 잴 수 있는 양이 아니라고 생각했기 때문이다. 우리는 현재 하이젠베르크의 생각이 지나치게 극단적이었던 것을 알고 있다. 입자의 궤도는 물론 정확하게 정의되지 않는데, 그 이유는 양자 요동이 있기 때문이다.

하지만, 아이러니하게도 하이젠베르크 방정식은 어떤 의미로는 고전역학과 가장 비슷한 관점이다. 뉴턴의 운동 방정식은 입자의 위치와 운동량이 시간의 함수로 어떻게 바뀌는지 알려준다. 하이젠베르크 방정식도 입자의 위치와 운동량을 비롯해서 관찰 가능한 물리량이 시간의 함수로 어떻게 바뀌는지 알려준다. 물론 이 과정에서 물리량이 보통의 숫자가 아니라 행렬로 확장되어야 한다는 조건이 있지만, 어찌 보면 파동 함수와 같이 아주 새로운 개념이 필요하지 않다. 더군다나 하이젠베르크 방정식은 뉴턴의 운동방정식과 매우 비슷하게 생겼다. 잠깐, 이게 무슨 소리인가 싶은 독자들이 있을 것이다.

겉보기에 뉴턴의 운동 방정식은 하이젠베르크 방정식과 전혀 비슷하지 않다. 하지만 약간의 수학적 작업을 통하면 뉴턴의 운동 방정식을 하이젠베르크 방정식과 매우 비슷한 모양으로 바꿀 수 있다. 이를 이해하기 위해서, 뉴턴의 운동 방정식을 새롭게 재수식화할 필요가 있다. 특히, “해밀토니안 역학^{Hamiltonian mechanics}”이라고 불리는 체계를 이해할 필요가 있다. 참고로, 이러한 고전적인 해밀토니안 역학에는 해밀토니안이라는 물리량이 나오는데, 연산자가 아니라는 성질만 빼고는 양자역학에 나오는 해밀토니안과 비슷하다. 다시 말해서, 해밀토니안은 본질적으로 에너지이다. 그런데 해밀토니안 역학이 뉴턴의 운동 방정식과 그 내용 면에서 정확히 같다면, 해밀토니안 역학은 도대체 왜 필요했던 것일까?

이 질문에 대한 가장 표준적인 답은 “해밀토니안 역학이 나중에 양자역학의 발전에 큰 도움이 되었다”이다. 그런데, 잠깐. 해밀토니안 역학은 양자역학이 나오기 한참 전에 만들어졌으므로 이 답은 말이 되지 않는다. 사실 해밀토니안 역학의 진가는 많은 입자들로 이루어진 다체계^{many-body system}의 동역학을 다루는 문제에서 발휘된다. 입자의 개수가 많지 않은 경우에는 뉴턴의 운동 방정식을 모든 입자에 대해서 적고 풀면 될 것이다. 하지만 입자의 개수가 약간만 많아지더라도 (심지어는 3개만 넘어도) 이런 작업은 실질적으로 불가능해진다. 이런 상황에서는 모든 입자의 움직임을 하나하나 따라가기 보다는 다체계의 전체적인 움직임을 통계적으로 다루는 것이 편리하게 된다. 해밀토니안 역학에서는 시스템의 동역학을 단순히 실공간에서의 움직임으로 보는 것이 아니라 위치 \(x\)와 운동량 \(p\)로 이루어진 확장된 “위상 공간^{phase space}”에서의 움직임으로 기술한다.

이 위상 공간 상의 움직임은 다음의 해밀토니안 방정식에 의해서 기술된다.\[\frac{dx}{dt}=\frac{\partial H}{\partial p}\]\[\frac{dp}{dt}=-\frac{\partial H}{\partial x}\]여기서 해밀토니안 방정식을 유도하지는 않을 것이다. 다만, 필자는 다시 한번 해밀토니안 방정식이 뉴턴의 운동 방정식과 정확히 같다는 사실을 강조하고 싶다. 이제 위치 \(x\)와 운동량 \(p\)에 의존하는 어떤 물리량 \(A(x,p)\)의 시간에 따른 변화를 알고 싶다고 하자.\[\frac{dA}{dt}=\frac{\partial A}{\partial x} \frac{dx}{dt} +\frac{\partial A}{\partial p}\frac{dp}{dt}\]위에서 필자는 미분의 연쇄 법칙^{chain rule}을 썼다. 위 공식에 해밀토니안 방정식을 적용하면 다음과 같은 결론에 도달한다.\[\frac{dA}{dt}=\frac{\partial A}{\partial x} \frac{\partial H}{\partial p} -\frac{\partial A}{\partial p}\frac{\partial H}{\partial x}=-\{H,A\}\]위에서 맨 마지막에 나오는 기호 \(\{f,g\}\)는 “푸아송 괄호^{Poisson bracket}”이라고 불리고 다음과 같이 정의된다.\[\{f,g\}=\frac{\partial f}{\partial x}\frac{\partial g}{\partial p}-\frac{\partial f}{\partial p}\frac{\partial g}{\partial x}\]정리하면, 뉴턴의 운동 방정식을 다음과 같이 적을 수 있다.\[\frac{dA}{dt}= -\{H,A\}\]자, 이제 위 방정식은 하이젠베르크 방정식과 비슷하게 보이는가? 왜 하필이면 양자역학에서의 교환자가 고전역학에서의 푸아송 괄호를 대체하는지 알 수 없으나, 두 개의 방정식 사이의 유사성은 놀랍다.

본 글의 맨 앞에 인용된 글을 눈여겨본 독자가 있는지 모르겠다. 글 초반에 더글라스 아담스의 “은하수를 여행하는 히치하이커를 위한 안내서”에 대해서 자세하게 설명했다. 본 글의 맨 앞에 인용된 글은 동일한 작가가 앞선 소설의 속편으로 쓴 “우주의 끝에 있는 레스토랑^{The Restaurant at the End of the Universe}”에서 나온 글 중의 하나이다. 우리말로 해석하면 다음과 같다.

“우주가 무엇을 위해, 그리고 왜 여기에 존재하는지 누군가가 정확히 알아낸다면,
그 순간 우주는 사라지고 훨씬 더 기괴하고 설명할 수 없는 그 어떤 것으로 대체될 것이라고
주장하는 이론이 있다. 이런 일이 벌써 벌어졌다고 주장하는 또 다른 이론도 있다.”

양자역학이 나오기 직전에 물리학자들은 우리가 알아야 할 모든 물리 법칙(고전역학, 전자기학, 열역학)은 이미 다 밝혀졌으며 이제부터는 이러한 물리 법칙을 최대한 정교하게 적용해서 우주의 작동 방식을 알아내는 일만 남았다고 생각했다. 심지어 적어도 원리적으로는 우주의 궁극적인 의미도 알아낼 수 있다고 생각했다. 하지만, 그 순간 우리가 알고 있던 물리 법칙의 근간이 무너지고 있었다. 더글라스 아담스가 주장한 것처럼 우주 자체가 실제로 고전역학적인 우주였다가 양자역학적인 우주로 대체된 것은 아닐 테지만, 적어도 물리학자들에게는 그들이 믿어 왔던 우주가 사라진 것이다. 수학적으로 표현하면, 고전역학적인 우주가 양자역학적인 우주로 대체된 순간은 바로 푸아송 괄호가 교환자로 대체된 순간이었다.

이제 드디어 양자역학의 세 가지 관점이 서로 같다는 것을 증명하려는 우리의 길다면 길고 짧다면 짧은 여정이 끝났다. “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”와 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”를 끝내며 우리의 여정이 어떻게 시작되었는지 기억을 되살려 보자. 필자는 “양자 삼위일체”를 설명하기 위해서 에셔의 “불가능한 삼각형”에 관한 이야기로 글을 시작했다. 필자가 생각하기에, 에셔의 “불가능한 삼각형”은 양자역학의 세 가지 관점이 처음에는 불가능해 보이지만 사실은 하나의 본질의 서로 다른 모습일 뿐이라는 사실을 가장 극적으로 보여준다. “불가능한 삼각형”은 언제나 필자에게 묘한 영감을 준다. 이번 글을 쓰면서, “불가능한 삼각형”이 주는 영감을 이용해 필자 자신의 로고도 만들어 보면 재미있겠다고 생각했다. 그래서 [그림 6]과 같은 로고를 만들어 보았다. 이 로고가 왜 필자를 나타내는 로고인지는 퀴즈로 남기겠다.