“I wish it need not have happened in my time.” said Frodo. “So do I.” said Gandalf, “and so do all who live to see such times. But that is not for them to decide. All we have to decide is what to do with the time that is given to us.”
-J.R.R. Tolkien, <The Fellowship of the Ring>
영화에서 자주 다루어지는 주제 중의 하나로 시간 여행이 있다. 많은 사람들이 좋아하겠지만 필자도 꽤 좋아하는 주제이다. 사람들은 왜 시간 여행에 관심이 많을까? 필자가 생각하기에, 시간 여행이라고 하면 원칙적으로 과거로 갈 수도 있고 미래로 갈 수도 있을 텐데 보통 과거로 돌아가는 얘기가 많은 데에서 실마리를 찾을 수 있다고 생각한다.
조금 더 구체적으로 말해서, 과거로 돌아가서 자신이 저지른 실수를 고치거나 미처 하지 못했던 일을 하는 이야기가 많다. 하지만 주인공 자신은 같은 사람이므로 과거로 돌아간다고 해도 단번에 실수를 제대로 고치거나 미처 하지 못했던 일을 원하는 대로 잘하기는 쉽지 않다. 그래도 여러 번 반복해서 시도하면 언젠가는 잘할 수 있지 않을까? 이런 상상에서 만들어진 영화의 시조 격으로 필자가 좋아하는 1993년에 개봉한 <그라운드호그 데이 Groundhog day>라는 영화가 있다. [그림1]은 <그라운드호그 데이>의 포스터이다. 참고로 이 영화는 국내에서 <사랑의 블랙홀>이라는 “창의적인” 이름으로 개봉되었다. 항상 그렇지만 스포일러 경고를 하고 시작한다.
영화 <그라운드호그 데이>의 주인공인 필 코너스Phil Connors는 미국 펜실베니아 주 피츠버그의 한 TV 방송국에서 기상 뉴스를 전달하는 기자이다. 그는 어느 날 우리나라 이름으로 “성촉절”이라고 불리는 2월 2일에 펜실베니아 주의 작은 시골 도시인 펑추토니Punxsutawney에서 열리는 그라운드호그 데이 축제에 프로듀서 리타Rita, 카메라맨 래리Larry와 함께 참석해서 기상 뉴스를 전달하라는 임무를 부여받는다. 그라운드호그는 땅속에 사는 마멋marmot이라는 다람쥐 과의 동물인데, 이 동물은 겨울잠에서 깨서 굴에서 나오다가 자기 그림자가 보이면 다시 겨울잠을 자러 들어간다는 전설이 있다. 전설에 따라 마멋을 굴에서 데리고 나와서 2월 2일에 겨울이 얼마나 지속될지 점을 치는 전통이 생겼는데, 이것이 축제로 발전한 것이 바로 그라운드호그 데이 축제이다.
원래부터 성격이 까칠했던 필은 취재를 마치자마자 펑추토니와 같은 작은 시골 도시에서 일분일초라도 더 시간을 보내는 것이 싫다며 즉시 떠나려 한다. 하지만 필은 갑자기 눈보라가 밀어닥쳐 고속도로가 폐쇄되는 바람에 하는 수 없이 펑추토니에서 하룻밤을 더 보내게 된다. 그런데 하룻밤을 자고 일어난 필은 전날 아침에 들었던 것과 정확히 똑같은 라디오 소리에 잠을 깨게 된다. 사실 필은 시간을 거슬러 전날 아침으로 되돌아온 것이다. 이때부터 필에게 정확히 같은 날이 계속 반복되기 시작한다. 소위 타임 루프time loop에 갇힌 것이다. 필 자신은 반복되는 모든 하루하루를 기억할 수 있지만 다른 사람들은 하루 동안만 기억할 수 있고 다음 날 아침에는 모든 사람들의 기억이 초기화된다.
이 영화의 특별한 점 중 하나는 필이 타임 루프에 갇힌 이유가 굳이 자세하게 설명되지 않는다는 점이다. 이로 인해서 관객들은 자기 자신이 필의 상황에 처하게 된 듯한 느낌을 갖게 된다. 그리고 필과 함께 미스터리를 따라가게 되는데, 그 재미가 쏠쏠하다.
처음에 무척 혼란스러웠던 필은 계속 반복되는 하루하루를 살아가면서 아무리 어처구니없는 실수를 해도 다시 처음으로 돌아가 새로운 하루가 시작된다는 사실을 깨닫는다. 자신이 저지른 행동에 아무런 결과가 없게 된 것이다. 신이 난 필은 이 상황을 은행 돈을 훔치거나 여자를 유혹하는 데에 적극적으로 이용하게 된다. 하지만 그것도 잠시. 이내 무기력함에 빠진 필은 자살함으로써 자신의 상황에서 탈출하려고 한다. 그렇지만 제아무리 어떻게 죽어도 필은 다시 살아나고, 똑같은 아침은 어김없이 반복된다. 이에 필은 본인이 불멸의 신이라고 생각하게 된다. 이 즈음에 처음에는 그저 재미있는 코미디라고 생각하고 보기 시작한 영화에 놀라운 분위기의 반전이 찾아온다.
필은 길거리에서 노숙자 할아버지를 한 명 만나는데 측은한 마음이 들어서 따뜻한 저녁을 사 주고 잘 대해 준다. 하지만 슬프게도 마지막 만찬을 얻어먹은 노숙자 할아버지는 곧 죽게 된다. 이에 필은 모든 방법을 동원해서 할아버지를 살리려고 하는데, 종국에는 아무리 그 어떤 노력을 해도 할아버지를 살려내는 것이 불가능하다는 사실을 깨닫게 된다. 영화의 톤이 묘하게 철학적으로 바뀌는 지점이다.
무한한 시간과 불멸의 능력이 주어지지만 그 사실을 자기 자신밖에 모른다. 그리고 이미 정해져 있는 운명은 바꿀 수 없다. 이러한 상황에서 인생의 의미는 무엇일까? 무한히 주어지는 시간에는 무엇을 하며 살아야 하는 것일까?
필은 그냥 하고 싶은 것을 하고, 배우고 싶은 것을 배우며 살기로 한다. 어려운 책을 읽고, 우연히 들리는 피아노 소리에 이끌려 피아노를 배우기 시작하고, 어려운 상황에 처한 사람들을 도와주고… 필은 그렇게 소박하지만 만족스러운 삶을 살기 시작한다. 어떤 이기적인 목적을 이루기 위해서가 아니라 순수하게 자신이 하고 싶은 일을 하고, 그 결과로 자연스럽게 남을 도움으로써 필은 만족감을 얻게 된 것이다. 필의 인생은 자연스러워졌고, 그렇게 되었을 때 필은 그동안 짝사랑하던 리타와 진정으로 가까워지게 된다. 아무 설명 없이 타임 루프에 갇혔던 것처럼 리타와 진정으로 사랑에 빠지자 필은 아무 설명 없이 타임 루프에서 빠져나와서 구원된다.
필자가 생각하기에 <그라운드호그 데이>가 우리에게 던지는 질문은 다음과 같다. 무한히 반복되는 시간이 주어진다면 무엇을 할 것인가? 왜 시간이 무한히 반복되는지 알면 좋을 것이다. 하지만 모른다 한들 바뀔 것은 없다. 진짜 중요한 것은 “주어진 시간에 무엇을 할 것인가?”이다. <그라운드호그 데이>는 이후 나온 수많은 영화에 깊은 영향을 주었다. 깊은 영향을 받은 영화들 중에서 필자가 특별히 좋아하는 몇 편을 고르자면 2011년에 개봉한 <소스 코드 Source Code>, 2013년에 개봉한 <어바웃 타임About Time>, 그리고 2014년에 개봉한 <엣지 오브 투모로우 Edge of Tomorrow> 등이 있다. 뉘앙스에 조금씩 차이가 있지만 타임 루프로 인해서 무한히 반복되는 시간에 무엇을 할 것인가가 역시 이들 영화의 화두이다.
양자역학에서도 반복되는 주제가 하나 있다. 그 주제는 파동 함수가 가지는 위상phase, 즉 위상각phase angle의 물리적 의미이다. 이전 연재 글에서 강조했듯이 파동 함수는 복소수이고, 그것의 절대값의 제곱은 입자가 주어진 위치에 존재할 확률을 준다. 그런데 만약에 확률이라는 단 하나의 숫자만 필요했다면 왜 자연은 굳이 복소수인 파동 함수까지 동원해야만 했던 것일까? 다시 말해서, 복소수는 실수 축과 허수 축으로 이루어진 2차원 평면에 존재하는 한 점이다. 따라서 복소수는 2개의 숫자, 길이와 방향으로 규정되어 진다. 물론 길이의 제곱은 주어진 위치에 존재할 확률을 준다. 그런데 방향, 즉 위상각은 도대체 어떤 물리적 의미를 가지는 것일까?
앞서 언급한 영화 <그라운드호그 데이>에서 왜 시간이 반복되는지 알 수 없듯이 우리는 진정으로 왜 위상각이 필요한지 알 수 없을지 모른다. 하지만 시간이 반복되는 이유보다 주어진 시간에 무엇을 할 것인가가 중요하듯이 위상각이 필요한 이유보다 위상각이 어떠한 역할을 하는가가 더 중요할 것이다.
이런 의미에서 보면 위상각은 설령 겉으로 드러나지 않을지언정 이미 그 존재만으로도 매우 중요한 역할을 하고 있다. 구체적으로, 필자가 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 설명했듯이, 위상각은 존재하되 겉으로 드러나지 말아야 하는 조건을 통해서 힘의 원리를 제공한다. 이 힘의 원리는 바로 “게이지 대칭성gauge symmetry”이다. 게이지 대칭성은 파동 함수의 위상각을 어떻게 선택하느냐에 상관없이 물리량에 변함이 없어야 한다는 성질이다. 그리고 이 성질은 우주를 지배하는 3가지 근본적인 힘인 전자기력electromagnetic force, 약력weak force, 강력strong force의 원리를 제공한다. 사실 이렇게 힘의 원리를 제공하는 것만으로도 위상각은 그 역할을 이미 충분히 다 하고 있는 것이다.
하지만 위상각의 역할은 근본적인 힘의 원리를 제공하는 것으로 끝나지 않는다. 역사적으로 보면 위상각이라는 화두는 반복해서 현대 물리학 연구의 중심으로 화려하게 귀환했다. 이것이 바로 이번 글의 제목이 “위상의 귀환return of the phase”인 이유이다.
위상각의 효과가 겉으로 드러나는 경우는 크게 두 가지로 나뉜다. 첫 번째는 게이지 대칭성이 아예 깨지는 경우이고, 두 번째는 게이지 대칭성이 깨지지 않으면서 위상각의 효과가 나타나는 경우이다.
여기에서 첫 번째 경우인 게이지 대칭성이 아예 깨지는 경우를 자세하게 설명하기는 쉽지 않다. 단도직입적으로 말해서, 게이지 대칭성이 깨지는 원리를 이해하기 위해서는 초전도체superconductor라는 물질 상태를 알아야 한다. 초전도체란 짧게 설명하면 전기 저항이 완벽하게 0인 도체이다. 어떻게 전기 저항이 완벽하게 0일 수 있을까? 그 무엇이든지 간에 자연에서 완벽하게 0이 되는 것이 가능하기는 한가? 사실 초전도체에 대한 이해는 초전도체가 아닌 일반적인 양자 물질 상태에 대한 이해가 깊어진 상태에서만 진정으로 얻어질 수 있다. 따라서 초전도체에 대한 설명은 조금 나중으로 미루도록 하자. 구체적으로 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 일반적인 양자 물질 상태에 대해서 설명을 하고, “믿기 힘든 양자 Incredible Quantum [12]: 많음, 다름, 그리고 양자”에서 초전도체를 비롯한 소위 “자발적 대칭성 붕괴spontaneous symmetry breaking”라는 현상에 대해서 설명을 할 예정이다. 관심있는 독자들은 그때까지 조금 기다려 주기를 부탁한다.
이번 글에서는 두 번째 경우인 게이지 대칭성이 깨지지 않으면서 위상각의 효과가 겉으로 드러나는 경우에 집중하기로 하자.
영의 이중 슬릿 실험
간단하게 말해서, 위상각은 여러 개의 파동이 중첩되어 서로 간섭interference을 일으킬 때, 그 효과를 드러낼 수 있다. 파동의 간섭 현상을 가장 잘 보여주는 실험으로 “영의 이중 슬릿 실험Young’s double slit experiment”이 있다. 이 실험에서 전자는 전자 빔 총electron beam gun에서 발사되어 각각의 슬릿slit을 통과한 후에 두 개의 파동으로 갈라진다. 두 개의 파동은 서로 다른 경로를 통해서 이동하는데, 그 경로에 따라서 위상각에 차이가 생긴다. 이러한 위상각의 차이는 최종 도착점인 스크린에서 두 개의 파동이 중첩될 때 간섭을 일으킨다. 실험의 개략적인 구조를 위해서 [그림2]를 참조하라.
수학적으로 간섭 패턴은 다음과 같이 이해할 수 있다. 앞에서 설명했듯이 전자의 파동은 슬릿을 통과한 후에 두 개의 서로 다른 파동으로 갈라지게 된다. 슬릿을 통과하고 난 후에 얻어지는 전자의 파동 함수는 수학적으로 어떻게 표현될까? 이 질문에 대한 답을 얻기 위해서 실제 물결이 비슷한 얇은 틈에 부딪힌다면 어떤 일이 발생할지 생각해 보자. 잘 생각해 보면 물결은 얇은 틈을 통과한 후에 출구를 중심으로 원형으로 퍼져 나갈 것이라는 것을 알 수 있다. 전자의 파동에도 비슷한 일이 발생한다. 구체적으로, 원형으로 퍼져 나가는 파동을 기술하는 파동 함수는 다음과 같이 주어진다.
\(\psi=e^{ikr}\)
위 수식에서 \(k\)는 파수wave number로서 파장wave length \(\lambda\)와 \(k=2\pi/\lambda\)의 관계식에 의해서 연결된다. 물론 \(r\)은 슬릿으로부터 주어진 위치까지의 거리이다. 참고로 이러한 파동을 전문적으로 원형파circular wave라고 부른다.
최종적으로 전자가 스크린에 도착하는 순간의 파동 함수는 이 두 원형파의 중첩 상태로 주어진다. 구체적으로, 첫 번째 슬릿에서 스크린의 한 점까지의 거리를 \(r_1\)이라고 하고 두 번째 슬릿에서 동일한 점까지의 거리를 \(r_2\)라고 할 때, 전자가 스크린의 한 점에 존재할 확률은 다음과 같이 주어진다.
\(|\psi|^2=|e^{ikr_1}+e^{ikr_2}|^2=2[1+\cos{(k\Delta r)}]=4\cos^2{(k\Delta r/2)}\)
위에서 \(\Delta r\)은 두 거리의 차이, 즉 \(\Delta r=r_1=r_2\)이다. 위에서 수식을 깔끔하게 정리하기 위해서 삼각함수 공식 하나를 썼는데, 그 공식은 \(1+\cos{\phi}=2\cos^2{(\phi/2)}\)이다. 결론적으로 전자가 스크린의 한 점에 존재할 확률은 두 경로 사이의 위상차인 \(k\Delta r\)에 의해서 결정된다.
이제 논의의 편의상 이중 슬릿이 뚫려있는 판과 스크린 사이의 거리인 \(L\)이 이중 슬릿 사이의 거리인 \(d\)보다 매우 크다고 가정하자. 이러한 가정 아래에서 약간의 삼각법trigonometry을 사용해 보면 \(\Delta r=d\sin{\theta}\)로 근사할 수 있다는 것을 알 수 있다. 여기서 \(\theta\)는 [그림2]에서 볼 수 있듯이 이중 슬릿 사이의 수직 중앙선에서 스크린의 주어진 점까지의 각도이다. 이제 스크린의 한 점에 전자가 존재할 확률은 다음과 같은 공식으로 주어진다.
\(|\psi|^2=4\cos^2{\left( \frac{\pi d \sin{\theta}}{\lambda}\right)}\)
위 공식은 전자가 스크린의 한 점에서 존재할 확률이 주기적으로 반복되는 패턴을 가진다고 알려준다. 특히, 확률이 국소적으로 최대가 되는 지점은 다음의 조건을 만족한다.
\(d\sin{\theta}=n\lambda\)
여기서 \(n\)은 정수이다. 이 조건은 다름 아니라 두 경로의 길이 차이가 파장의 정수배가 되는 조건으로, 두 경로로 갈라진 전자의 파동은 서로 보강 간섭constructive interference을 일으킨다. 반대로 다음과 같은 조건이 만족되면 확률은 국소적으로 최소가 된다.
\(d\sin{\theta}=\left(n+\frac{1}{2}\right)\lambda\)
이 조건은 두 경로의 길이 차이가 파장의 반정수 배가 되는 조건으로, 이 경우에는 두 파동이 상쇄 간섭destructive interference을 일으키게 된다.
여기서 기억해야 할 굉장히 중요한 사실이 하나 있다. 그것은 이중 슬릿 실험에서 간섭을 일으키는 대상이 바로 두 경로로 갈라진 전자 자기 자신의 파동 함수라는 사실이다. 만약에 간섭을 일으키는 대상이 서로 다른 전자의 파동 함수라면 이 현상은 어떻게 해서 고전역학적으로 이해할 수 있을지 모른다. 하지만 양자역학은 우리에게 단 하나의 전자가 있더라도 그 자기 자신의 파동 함수가 두 경로로 갈라진 후에 서로 간섭을 일으킬 수 있다고 말해준다. 언뜻 들으면 모순적인 것처럼 느껴지는 이 현상은 양자역학의 가장 특징적인 성질 중의 하나이다.
이것을 실험적으로 증명하기 위해서 어떻게 해야 할까? 답은 원칙적으로 쉽다. 전자를 전자 빔 총에서 한 번에 한 개씩 발사하는 것이다. 물론 이렇게 하면 단번에 제대로 된 간섭 패턴이 나오지 않을 것이다. 하지만 전자를 계속해서 한 개씩 발사하다가 보면 간섭 패턴이 서서히 형성되기 시작한다. [그림3]은 이렇게 서서히 형성되는 전자의 간섭 패턴을 보여준다. 정말 놀랍지 않은가?
두 경로로 갈라진 전자 자기 자신의 파동 함수가 서로 간섭을 일으킨다는 사실은 매우 놀랍다. 그런데 어찌 보면 이보다 더 놀라운 현상이 아직 우리를 기다리고 있다. 이 현상은 각각의 슬릿을 통과해서 이동하는 두 경로 사이에 자기장이 존재하는 경우에 발생한다.
“믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 설명하기를 자기장의 존재는 벡터 퍼텐셜vector potential을 소용돌이치게 한다고 했다. 이 벡터 퍼텐셜의 소용돌이는 서로 다른 두 경로 사이에 여분의 위상각 차이를 야기할 수 있고, 결과적으로 간섭 패턴에 변화를 일으킬 수 있다. 이 현상의 이름은 바로 그 유명한 “아하로노브-봄 효과Aharonov-Bohm effect”이다. 아하로노브-봄 효과가 유명한 이유는 앞서 설명한 근본적인 힘의 원리인 게이지 대칭성과 깊게 연관되기 때문이다. 위상의 귀환이다!
아하로노브-봄 효과
자기장은 일반적으로 항상 위상각에 영향을 미친다. 하지만 아하로노브-봄 효과가 얼마나 신기한지 이해하기 위해서 조금 극단적인 상황을 생각해 보자. 즉, 자기장이 공간의 작은 한 구역에 국한되어 있어서 전자가 실제로 이동하는 경로에는 그 값이 정확히 0인 상황을 상상해 보자. 구체적으로 이러한 상황은 매우 가늘고 긴 솔레노이드solenoid가 있으면 실제로 구현된다. 아하로노브-봄 효과를 주는 실험 상황의 개략도를 위해서 [그림4]를 참조하라. 이 상황에서 자기장은 완벽하게 솔레노이드 안에 갇혀 있게 된다. 여기서 중요한 것은 자기장 자체는 솔레노이드 안에 갇혀 있지만 자기장으로 인해서 소용돌이치는 벡터 퍼텐셜은 그 바깥에도 존재할 수 있다는 사실이다. 그리고 이 벡터 퍼텐셜의 소용돌이는 위상각에 영향을 미칠 수 있다.
위에서 설명한 내용을 수학적으로 표현하면 다음과 같다. “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 필자는 벡터 퍼텐셜이 있을 때 역학적 운동량mechanical momentum은 카노니칼 운동량canonical momentum과 벡터 퍼텐셜의 차이로 주어진다고 했다.
\(m{\bf v}={\bf p}-\frac{e}{c}{\bf A}\)
이제 위에서 가정한 대로 자기장이 공간적으로 아주 국한되어서 전자의 경로에 전혀 영향을 주지 않는다고 하자. 이 가정하에서 전자의 파동은 기본적으로 솔레노이드가 없을 때와 똑같은 파동으로 주어질 것이다. 다시 말해서, 카노니칼 운동량 \({\bf p}\)는 벡터 퍼텐셜이 없을 때와 동일하게 \(\hbar {\bf k}\)가 될 것이다.
하지만 실제로 물리적인 의미를 지니는 운동량은 카노니칼 운동량이 아니라 역학적 운동량이다. 역학적 운동량에 벡터 퍼텐셜 성분이 있다는 사실은 평면파의 위상각에 파수뿐만 아니라 벡터 퍼텐셜에 의한 효과가 더해져야 한다는 것을 의미한다. 여기서 엄밀하게 유도할 수는 없지만, 역학적 운동량의 정의를 곰곰이 살펴보다 보면 벡터 퍼텐셜이 위상각에 미치는 효과는 다음과 같이 파수를 새롭게 치환하면 얻을 수 있다는 영감을 받을 수 있다.
\({\bf k} \rightarrow {\bf k}-\frac{e}{\hbar c}{\bf A}\)
이 치환 방법은 응집물질 분야에서 이 방법을 본격적으로 사용한 물리학자인 루돌프 파이얼스Rudolf Peierls의 이름을 따서 “파이얼스 치환Peierls substitution”이라고 불린다.
파이얼스 치환을 사용하면 벡터 퍼텐셜이 있는 경우에 두 경로 사이의 위상각 차이를 다음과 같이 얻을 수 있다.
\(\Delta \phi=\phi_1 – \phi_2=\int_{\rm path 1} \left({\bf k}-\frac{e}{\hbar c}{\bf A} \right)\cdot d{\bf l}-\int_{\rm path 2} \left({\bf k}-\frac{e}{\hbar c}{\bf A} \right)\cdot d{\bf l}\)
여기서 “path1”과 “path2”가 아래 첨자로 붙어있는 적분 기호는 각각 1번과 2번 경로를 따라가면서 적분을 수행한다는 의미이다. 이제 앞선 섹션의 설명에 따라서 파수 성분에 의한 위상각의 차이가 \(k\Delta r\)인 것을 기억하면 위 공식은 다음과 같이 쓰일 수 있다.
\(\Delta \phi=\phi_1 – \phi_2=k\Delta r -\frac{e}{\hbar c}\oint{\bf A}\cdot d{\bf l}\)
위에서 동그라미가 중간에 끼워져 있는 적분 기호 \(\oint\)는 1번과 2번 경로를 하나로 묶어서 1번 경로로 스크린까지 갔다가 다시 2번 경로를 따라서 전자 빔 총으로 되돌아오는 소위 “닫힌 경로closed path”를 따라가면서 적분을 수행한다는 의미이다.
계속 논의를 이어가기에 앞서 한 가지 강조하고 넘어갈 부분이 있다. 게이지 대칭성을 깨지 않으면서 위상각의 효과가 겉으로 드러나는 경우에는 위상각의 값 자체는 물리적인 의미를 가지지 않는다. 위상각의 값 자체가 아니라 위상각의 차이가 중요한데, 앞서 설명한 예에서 위상각의 효과가 항상 서로 다른 두 경로 사이의 간섭이라는 형태로 나타난다는 사실에 주목하라. 서로 다른 두 경로가 한 점에서 만나는 상황을 다르게 보면 주어진 원점에서 출발해서 중간 경유지를 거쳐 다시 원점으로 돌아오는 하나의 긴 여정이라고 볼 수 있다. 위에서 언급했듯이 이렇게 처음과 끝이 맞닿아 있는 경로를 닫힌 경로라고 부른다. 이러한 닫힌 경로에 대해서 정의된 위상각만이 물리적으로 의미가 있다. 전문적으로 말해서, 닫힌 경로에 대해서 정의된 위상각은 게이지 변환에 대해서 불변이다.
이제 다시 본론으로 돌아가 보자. 곰곰이 생각해 보면 벡터 퍼텐셜을 주어진 닫힌 경로를 따라가면서 적분한다는 것은 벡터 퍼텐셜이 그 경로를 따라서 얼마나 강하게 소용돌이치고 있는가를 계산하는 것과 같다. 수학적으로 말하면, 주어진 닫힌 경로를 따라가면서 어떤 벡터 함수를 적분하는 것은 그 벡터 함수의 컬curl 미분값을 닫힌 경로의 내부에 대해서 모두 다 더하는 것과 같다. 이 수학적 사실은 “스토크스의 정리Stokes’ theorem”라고 알려져 있다. 벡터 함수의 컬 미분은 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 어느 정도 자세하게 설명했으니 혹시 기억이 나지 않는 독자들은 참고하기를 부탁한다.
그런데 벡터 퍼텐셜의 컬 미분은 자기장이다. 따라서 위 닫힌 경로를 따라가면서 벡터 퍼텐셜을 적분한 값은 바로 그 경로 안에 담겨있는 자기장의 총 합인 “자기 선속magnetic flux” 이다. 자기 선속은 줄여서 흔히 “자속”이라고 불린다. 이 자속을 \(\Phi\)라고 할 때 앞선 두 경로 사이의 위상각 차이는 다음과 같이 정리된다.
\(\Delta \phi=k\Delta r -e\Phi/\hbar c\)
따라서 벡터 퍼텐셜이 있는 경우에 전자의 간섭 패턴의 공식은 다음과 같이 수정된다.
\(|\psi|^2=4\cos^2{\left( \frac{\pi d \sin{\theta}}{\lambda} -\frac{e\Phi}{2\hbar c} \right)}\)
이 공식에 따르면 전자의 간섭 패턴은 매우 가늘고 긴 솔레노이드 안에 갇힌 자기장에 영향을 받는다. 그런데 조금 이상하지 않은가? 앞서 가정했듯이 자기장은 완벽하게 솔레노이드 안에 갇혀 있기 때문에 전자를 직접 건드릴 수 없다. 하지만 자기장은 벡터 퍼텐셜을 소용돌이치게 할 수 있고, 이 벡터 퍼텐셜의 소용돌이는 위상각을 통해서 전자의 간섭 패턴에 영향을 줄 수 있다. 놀랍게도 양자역학적으로 보면 자기장보다 벡터 퍼텐셜이 더 물리적으로 의미가 있는 것이다!
물론 솔레노이드 안에 갇힌 자기장이 항상 간섭 패턴에 영향을 줄 수 있는 것은 아니다. 위 공식에서 자속이 \(\hbar c/e\)의 단위로 \(2\pi\)의 정수배가 된다면, 다시 말해서 \(e\Phi/\hbar c=2n\pi\)라면 자기장은 간섭 패턴에 아무런 영향을 미치지 못하게 된다. 플랑크 상수 \(h\)가 \(2\pi\hbar\)인 것을 감안해서 다시 말하면, 자속이 \(hc/e\)의 정수배가 될 때마다 자기장은 아무런 역할을 하지 않게 된다. 정수배가 된다는 것은 다른 말로 하면 양자화가 된다는 말이다. 따라서 앞서 언급된 \(hc/e\)라는 값은 자속의 특별한 양자 단위라고 볼 수 있다. 이 값의 이름은 “자속 양자magnetic flux quantum”이다. 편의상 자속 양자를 앞으로 \(\phi_0\)로 표기하기로 하자. 결론적으로 자속이 자속 양자의 정수배가 될 때마다 우리의 가늘고 긴 솔레노이드는 물리적으로 아무런 역할도 하지 않게 된다.
자, 이제 자속 양자의 정수배인 자속을 내부에 품고 있는 우리의 가늘고 긴 솔레노이드가 무한히 가늘어지는 극한을 상상해 보자. 이 솔레노이드는 무한히 가늘기 때문에 보이지 않고 주변에 입자가 있다고 하더라도 충돌할 수 없다. 또한 내부에 품어져 있는 자속은 자속 양자의 정수배이기 때문에 입자들의 간섭 패턴에도 아무런 영향을 줄 수 없다. 그야말로 측정할 수 없는 유령과 같은 존재이다. 그런데 이 상상 속 무한히 가는 솔레노이드에는 특별한 이름이 붙어 있다. 그 이름은 바로 “디랙 끈Dirac string”이다.
도대체 왜 이렇게 아무런 역할도 하지 않는 상상 속의 물체에 특별한 이름이 붙어 있는 것일까?
디랙 끈
폴 디랙Paul Dirac은 어느 날 “우주에 존재하는 (혹은 그때까지 발견된) 모든 입자의 전기 전하electric charge는 왜 반드시 전자의 전기 전하의 정수배로 양자화되는 것일까?”라는 의문을 갖게 된다. 물론 원자핵을 구성하고 있는 양성자proton의 전기 전하가 전자의 전기 전하의 정수배가 아니라면 전체 원자의 전기 전하를 정확히 0으로 만들기가 쉽지 않을 것이다. 그리고 그렇다면 우주는 현재 우리가 알고 있는 것과는 매우 다른 모습을 지닐 것이다. 예를 들어 모든 기체는 플라즈마plasma와 같이 이온ion들이 떠다니는 상태가 될 것이다. 왠지 숨을 쉬기가 매우 힘들 것 같다는 생각이 드는 것은 필자뿐일까? 물론 숨을 쉴 수 있는 인간을 포함한 생명체가 아예 존재하지 못할 확률도 매우 클 것이다.
위에서 제시된 설명에도 어느 정도 그럴싸한 면은 있다. 하지만 디랙의 아이디어는 조금 특별했다. 그의 아이디어의 결론부터 말하면 다음과 같다. 우주에 자기 홀극magnetic monopole이 단 하나라도 존재한다면 우주에 존재하는 모든 입자의 전기 전하는 양자화되어야 한다. 이 무슨 황당한 소리일까 싶지만 일단 그 스케일에 있어서 놀라지 않을 수 없다. 자기 홀극은 아직까지 실험적으로 발견되지 않았다. 하지만 방대한 우주 어딘가에 자기 홀극이 하나쯤은 존재하지 않을까? 그리고 그렇다면 우주에 존재하는 모든 입자의 전기 전하는 양자화된다. 정확히 언제였는지 기억나지는 않지만 필자가 이 내용을 처음 배웠을 때 느꼈던 놀라움은 아직도 생생하다. 자, 이제 디랙이 어떻게 이러한 결론에 이를 수 있었는지 구체적으로 살펴보자. 아주 어려울 것 같지만 사실은 우리가 지금까지 해 놓은 정지 작업이면 충분히 이해할 수 있다.
우선 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 설명했듯이 맥스웰의 방정식에 따르면 자기 홀극은 존재할 수 없다. 구체적으로, 맥스웰의 4가지 방정식 중에서 자기장의 다이버전스divergence가 0이라는 방정식이 바로 자기 홀극이 없다는 조건을 제시한다. 물론 이것은 실험적인 사실에 근거한 것으로 만약에 자기 홀극이 발견된다면 맥스웰의 방정식은 수정되어야 할 것이다. 어쨌든 우리가 현재 아는 한 자기 홀극은 존재하지 않는다. 하지만 사실은 현재 우리에게 주어진 맥스웰의 방정식을 수정하지 않고도 자기 홀극이 존재할 수 있는 방법이 단 하나 있다. 그 방법은 바로 디랙 끈을 이용하는 방법이다!
디랙 끈은 자속 양자의 정수배인 자속을 내부에 품고 있는 무한히 가는 솔레노이드이다. 앞선 논의에서 우리는 매우 가늘고 긴 솔레노이드의 중간 즈음에서 무슨 일이 일어나는가에 집중했다. 이제 이러한 솔레노이드의 양 끝 부분에서 무슨 일이 일어나는지 생각해 보자. 솔레노이드의 내부를 통해서 흐르던 자기장 다발은 솔레노이드의 끝에 도달해서는 밖으로 쏟아져 나오게 될 것이다. 그리고 이렇게 쏟아져 나온 자기장은 솔레노이드의 끝점을 중심으로 모든 방향으로 균등하게 퍼져 나오게 될 것이다. 전체 자기장의 총량, 즉 자속이 고정된 상태에서 자기장이 모든 방향으로 균등하게 퍼져 나온다는 것은 자기장이 다음과 같은 역제곱 법칙inverse square law에 의해서 기술된다는 것을 의미한다.
\({\bf B}=\frac{g}{r^2}\hat{r}\)
여기서 \(r\)은 솔레노이드의 끝점으로부터 주어진 위치까지의 거리이고, \(\hat{r}\)은 \(r\)이 커지는 방사 방향radial direction을 가리키는 단위 벡터이다. \(g\)는 기본적으로 전체 자기장의 총량으로 구 표면의 면적이 \(4\pi r^2\)이라는 사실을 감안하면 \(4\pi g=\Phi\)임을 알 수 있다.
그런데 가만히 생각해 보면 솔레노이드의 끝점에서 방사 방향으로 퍼져 나오는 자기장을 기술하는 역제곱 법칙은 전기 전하에서 방사 방향으로 퍼져 나오는 전기장을 기술하는 역제곱 법칙과 정확하게 같은 수학적인 형태를 지닌다. 따라서 무한히 가는 솔레노이드의 끝점은 실질적으로 “자기 홀극”이라고 볼 수 있다. 이러한 관점에서 보면 \(g\)는 자기장의 세기를 결정하는 “자기 전하magnetic charge”이다. [그림5]를 참조하라.
다만 솔레노이드의 끝점으로 이루어진 이 “자기 홀극”은 단독으로 존재할 수 없고, 항상 서로 반대의 자기 전하를 지니는 한 쌍이 솔레노이드로 연결된 상태로 존재해야 한다. 하지만 이러한 상황을 피할 수 있는 방법이 단 하나 있다. 그것은 바로 솔레노이드 내부에 담겨 있는 자속이 자속 양자의 정수배가 되는 것이다. 이 경우에는 앞서 설명했듯이 솔레로이드가 물리적으로 아무런 역할도 하지 않게 된다. 다시 말하면 2개의 자기 홀극을 연결하고 있던 솔레노이드가 사라지게 되어 각각의 자기 홀극이 자유롭게 되는 것이다. 진정한 의미로 자기 홀극이 존재할 수 있게 되는 것이다.
위 조건을 수학적으로 정리하면 다음과 같다. 우선, 자기 전하 \(g\)와 자속 \(\Phi\)의 관계는 \(4\pi g=\Phi\)이다. 그리고 자속이 자속 양자의 정수배라는 조건은 \(\Phi=n\phi_0\)로 표시된다. 따라서 \(g\)는 다음과 같이 양자화된다.
\(g=n\frac{\phi_0}{4\pi}\)
이 공식의 일반적인 해석은 디랙 끈 내부에 담겨 있는 자속이 양자화되어야 한다는 것이다.
사실 위에서 자속이 양자화된다는 예측은 실제로 실험적으로 관측되었다. 여기서 자세하게 설명할 수는 없으나 소위 제2종 초전도체type-II superconductor를 두께가 얇은 판으로 만들어서 자기장을 수직으로 걸면 자기장이 마치 눈에 보이지 않는 솔레노이드에 갇힌 것과 같이 다발의 형태로 초전도체를 투과할 수 있다. 이때 자기장 다발의 총 자속은 기본적으로 위 공식에 의해서 양자화된다. 유일한 차이는 전자의 전기 전하 대신 정확히 2배의 전기 전하가 들어간다는 사실이다. 그 이유는 초전도체 내부에서는 전자 2개가 결합하여 “쿠퍼 쌍Cooper pair”이라고 불리는 전자쌍이 흘러 다니기 때문이다. 자세한 설명은 나중에 이어질 “믿기 힘든 양자 Incredible Quantum [12]: 많음, 다름, 그리고 양자”에서 주어질 예정이다.
그런데 평범하지 않았던 디랙은 위 공식을 전혀 다른 방식으로 해석했다. 우선, 자속 양자의 정의를 이용해서 위 공식을 다음과 같이 다시 쓰자.
\(ge=n\frac{hc}{4\pi}\)
그런데 이 공식은 단순히 전자뿐만 아니라 우주의 모든 입자의 경우에도 동일하게 적용되어야 한다. 따라서 전자의 전기 전하 \(e\)를 일반적인 입자의 전기 전하 \(q\)로 치환하여 위 공식을 다음과 같이 다시 써 보자.
\(q=n\frac{hc}{4\pi g}\)
이제 우주 어딘가에 자기 홀극이 하나 존재하고 그것의 자기 전하가 \(g\)라고 하면 우주에 존재하는 모든 입자의 전기 전하는 위 공식에 의해서 양자화되어야 한다! 앞서 언급했듯이 참 스케일이 장대한 예측이다.
하지만 문제는 자기 홀극이 지금까지 발견된 적이 없다는 사실이다. 적어도 실공간real space에서 입자의 형태로 발견된 적은 없다. 하지만 자기 홀극은 실공간에 존재하는 입자가 아닌 다른 형태로 존재할 수 있다. 물리학의 관점에서 보면 어떤 두 물체가 다르게 보이더라도 정확히 같은 물리 법칙에 의해서 기술된다면 그 둘은 본질적으로 같은 것이다. 이런 관점에서 자기 홀극은 실공간은 아니지만 스핀 공간spin space에 존재한다.
스핀의 회전
스핀 공간에 자기 홀극이 존재한다는 사실은 의외의 곳에서 실마리가 발견된다. 이 실마리를 얻기 위해서는 스핀의 회전 운동에 대해서 이해해야 한다. 그리고 스핀의 회전 운동을 이해하기 위해서는 먼저 실공간에서의 회전 및 병진 운동에 대해서 이해해야 한다. 가장 쉬운 실공간에서의 병진 운동으로부터 이야기를 시작하기로 하자.
편의상 1차원의 실공간에 파동 함수 \(f(x)\)가 주어져 있다고 하자. 우리의 목표는 이 파동 함수를 옆으로 \(\delta x\)만큼 병진 운동, 즉 평행 이동시키는 것이다. 사실 \(f(x)\)의 함수 모양이 정확히 알려져 있다면 답은 간단하다. 평행 이동된 파동 함수는 바로 \(f(x-\delta x)\)이다. 그런데 우리의 진짜 목표는 이 평행 이동된 파동 함수 \(f(x-\delta x)\)를 원래의 파동 함수 \(f(x)\)에 어떤 연산자를 작용해서 얻는 것이다. 특이한 목표라고 생각할 수 있지만 사실 이 목표를 만족하는 연산자는 매우 잘 알려져 있다. 다시 말해서, \(f(x-\delta x)\)는 테일러 급수Taylor series를 통해서 다음과 같이 전개될 수 있다.
\(f(x-\delta x)= f(x)+f^\prime(x)(-\delta x)+\frac{1}{2}f^{\prime\prime}(x)(-\delta x)^2+\cdots+\frac{1}{n!}f^{(n)}(x)(-\delta x)^n+\cdots\)
위 공식은 미분 연산자의 급수가 파동 함수에 적용되는 형식으로 다음과 같이 다시 표현될 수 있다.
\(f(x-\delta x)= \left[ 1-\delta x \frac{d}{dx}+\frac{1}{2}\left(-\delta x \frac{d}{dx} \right)^2+\cdots+\frac{1}{n!}\left(-\delta x \frac{d}{dx}\right)^n+\cdots \right] f(x)\)
이제 위 공식을 자세히 살펴보면 아주 흥미로운 사실을 하나 깨달을 수 있다. 그것은 대괄호 안에 담긴 표현이 다름 아닌 바로 지수 함수exponential function를 나타내는 급수라는 것이다. 다시 말해서 지수 함수의 급수 표현을 이용해서 위 공식은 다음과 같이 다시 쓰일 수 있다.
\(f(x-\delta x)= e^{-\delta x \left(\frac{d}{dx}\right)} f(x)\)
이제 미분 연산자가 기본적으로 운동량 연산자라는 성질, 즉 \(\hat{p}=-i\hbar\left( \frac{d}{dx} \right)\)를 이용하면 위 공식을 다음과 같이 최종적으로 다시 쓸 수 있다.
\(f(x-\delta x)= e^{-\frac{i}{\hbar} \delta x \hat{p}} f(x)\)
위 공식이 의미하는 바는 무엇인가?
위 공식은 양자역학에서 매우 중요한 함의를 갖고 있다. 위 공식이 의미하는 바를 말로 풀어서 쓰면 다음과 같다.
“운동량을 변수로 가지는 지수 함수는 실공간에서 병진 운동을 일으키는 연산자이다.”
그런데 잘 생각해 보면 운동량이란 실공간에서 “병진 운동의 세기”를 재는 물리량이다. 이제 이 관찰 결과를 다음과 같은 일반적인 아이디어로 확장해 볼 수 있다.
“어떤 운동의 세기를 재는 물리량을 변수로 가지는 지수 함수는 바로 그 운동을 일으키는 연산자이다.”
이 아이디어를 적용할 수 있는 첫 번째 중요한 예는 실공간에서의 회전 운동이다.
실공간에서 회전 운동의 세기를 재는 물리량은 각운동량, 엄밀하게 말해서 궤도 각운동량orbital angular momentum이다. 따라서 위 아이디어에 따르면 실공간에서 회전 운동을 일으키는 연산자는 궤도 각운동량을 변수로 가지는 지수 함수이다. 구체적으로, 실공간에 주어진 입자를 \(z\) 축을 중심으로 \(\theta\)만큼 회전시키는 연산자는 다음과 같다.
\(U_z(\theta)=e^{-\frac{i}{\hbar}\theta \hat{L}_z}\)
비슷하게 각각 \(x\)와 \(y\) 축을 중심으로 \(\theta\)만큼 회전시키는 연산자는 다음과 같이 쓰인다.
\(U_x(\theta)=e^{-\frac{i}{\hbar}\theta \hat{L}_x}\)
\(U_y(\theta)=e^{-\frac{i}{\hbar}\theta \hat{L}_y}\)
비슷하게 스핀의 회전 운동의 세기를 재는 물리량은 스핀 각운동량이다. 따라서 스핀을 회전시키는 연산자는 궤도 각운동량을 스핀 각운동량으로 바꾸기만 하면 얻을 수 있다. “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명하기를 전자의 스핀 각운동량은 기본적으로 파울리 행렬Pauli matrix이다. 구체적으로 전자의 스핀 각운동량은 다음과 같이 주어진다.
\(S_i=\frac{\hbar}{2} \sigma_i\)
여기서 \(i\)는 \(x, y, z\)를 의미한다. 파울리 행렬의 구체적인 형태는 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”를 참조하기를 바란다. 결론적으로 파울리 행렬을 이용하면 스핀을 회전시키는 연산자를 다음과 같이 쓸 수 있다.
\(U_i(\theta)=e^{-\frac{i}{2}\theta \sigma_i}\)
위 공식이 바로 우리의 최종 목표인 스핀 회전 연산자이다.
이제 위 공식을 이용하면 주어진 스핀 상태를 원하는 축을 중심으로 원하는 각도만큼 회전시킬 수 있다. 예를 들어서, \(z\) 축으로 스핀 업인 상태를 \(x\) 축을 중심으로 \(\theta\)만큼 회전시켜 보자. 수학적으로 이 작업은 다음과 같이 표현된다.
\(|\psi\rangle= e^{-\frac{i}{2}\theta \sigma_x}|\uparrow\rangle\)
여기서 \(|\uparrow\rangle\)은 \(z\) 축으로 스핀 업인 상태를 나타내는 켓 벡터ket vector이다. 브라-켓 표기법은 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 자세하게 설명했다. 참고로 \(|\uparrow\rangle\)은 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 \(z\) 축 방향으로 스핀 업인 상태라는 것을 강조하기 위해서 \(|z,+\rangle\)라고 표기되었다. 따라서 \(|z,+\rangle\)을 일반적인 벡터 형식으로 쓰면 다음과 같다.
\(|\uparrow\rangle=\left(\begin{array}{c}1 \\0\end{array}\right)\)
이즈음에서 물리적인 직관을 얻기 위해서 스핀이 마치 나침반의 바늘처럼 진짜 화살표로 표현될 수 있다고 상상해 보자. 이 상상에서 화살표의 방향은 스핀의 방향을 표시한다. 즉, 화살표가 \(z\) 축 방향을 가리키는 것은 스핀이 \(z\) 축으로 스핀 업인 상태라는 것을 의미한다. 물론 화살표를 회전시키는 것은 스핀을 회전시키는 것에 해당한다. 이제 위에서 스핀을 회전시키는 상황을 개략도로 그리면 [그림6]이 된다. 이제 숙제는 \(2\times 2\) 행렬인 파울리 행렬을 변수로 가지는 지수 함수를 계산하는 것이다.
“행렬을 변수로 가지는 지수 함수”라는 말은 처음 들으면 매우 당황스러운 말이다. 도대체 이런 함수를 어떻게 계산할 수 있을까? 다행히 우리는 지수 함수를 테일러 급수로 전개할 수 있다. 급수는 곱으로 이루어져 있고 우리는 행렬을 곱할 수 있다. 이 방법을 쓰면 우리는 스핀 회전 연산자를 다음과 같이 쓸 수 있다.
\(U_i(\theta)=e^{-\frac{i}{2}\theta \sigma_i}=\cos{\left(\frac{\theta}{2}\right)}I –i \sin{\left(\frac{\theta}{2}\right)}\sigma_i\)
위에서 \(I\)는 항등 행렬identity matrix이다. 여기서 자세한 유도 과정을 기술하지는 못하지만 위 공식은 파울리 행렬이 두 번 곱해지면 항등 행렬이 된다는 성질을 이용하면 유도할 수 있다. (재미있게도 위 공식은 “믿기 힘든 양자 Incredible Quantum [2]: 가장 순수한 형태의 파동”에서 설명한 오일러의 공식과 굉장히 유사하다!)
이제 위 공식을 이용해서 \(x\) 축을 중심으로 \(\theta\)만큼 회전시키는 스핀 회전 연산자를 구체적으로 쓰면 다음과 같다.
\(U_x(\theta) =\left(\begin{array}{cc}\cos{\left(\frac{\theta}{2}\right)} & -i\sin{\left(\frac{\theta}{2}\right)} \\-i\sin{\left(\frac{\theta}{2}\right)} & \cos{\left(\frac{\theta}{2}\right)}\end{array}\right)\)
자, 이제 위 스핀 회전 연산자가 제대로 스핀을 회전시키는지 알기 위해서 테스트를 하나 해 보자. [그림6]에서 추측할 수 있듯이 \(|\uparrow\rangle\)을 \(x\) 축을 중심으로 270도, 즉 라디안radian으로 \(3\pi/2=-\pi/2\)만큼 회전시키면, 스핀 상태는 \(y\) 축으로 스핀 업인 상태가 되어야 한다. 이 추측이 맞는지 알아보자.
\(U_x(-\pi/2)|\uparrow\rangle =\left(\begin{array}{cc}\cos{\left(\frac{\pi}{4}\right)} & i\sin{\left(\frac{\pi}{4}\right)} \\i\sin{\left(\frac{\pi}{4}\right)} & \cos{\left(\frac{\pi}{4}\right)}\end{array}\right)\left(\begin{array}{c}1 \\ 0\end{array}\right)= \frac{1}{\sqrt{2}} \left(\begin{array}{cc}1 & i \\ i & 0\end{array}\right)\left(\begin{array}{c}1 \\ 0\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ i\end{array}\right)\)
위 스핀 상태는 우리가 추측한 대로 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 유도된 바가 있는 \(y\) 축으로 스핀 업 상태인 \(|y,+\rangle\)이다!
자, 이제 스핀을 회전시키는 김에 완전히 한 바퀴, 즉 360도 회전시켜서 원래 스핀 상태로 돌려 보자. 왜 이런 쓸데없는 짓을 하는가 궁금하겠지만 일단 해 보자. 360도는 라디안으로 \(2\pi\)이므로 위에서 수행한 것과 유사한 작업을 수행하면 다음과 같은 결론에 도달한다.
\(U_x(2\pi)|\uparrow\rangle =\left(\begin{array}{cc}\cos{\left(\pi\right)} & i\sin{\left(\pi\right)} \\i\sin{\left(\pi\right)} & \cos{\left(\pi\right)}\end{array}\right)\left(\begin{array}{c}1 \\ 0\end{array}\right)= \left(\begin{array}{cc}-1 & 0 \\ 0 & -1\end{array}\right)\left(\begin{array}{c}1 \\ 0\end{array}\right)=-\left(\begin{array}{c}1 \\ 0\end{array}\right)=-|\uparrow\rangle\)
앗, 이상한 일이 벌어졌다! 스핀 상태가 원래 상태로 돌아가지 않고 그 앞에 마이너스 부호가 붙었다. 처음 보면 별거 아닌 것 같지만 잘 생각해 보면 심각한 상황이다. 물리적으로 말해서 스핀을 한 바퀴 회전시키고 나면 원래 자기 자신의 파동 함수와 상쇄 간섭을 일으킬 수 있다. 스핀 상태는 360도가 아닌 그것의 두 배인 720도를 돌리면 원래대로 돌아온다. 도대체 왜 이런 일이 벌어진 것일까?
표준적인 설명 방식에 따르면 이런 이상한 일이 벌어진 이유는 스핀의 회전이 소위 SU(2)라고 불리는 특별한 대수 구조를 지니고 있기 때문이다. 수학을 잘 아는 독자에게는 이 표준적인 설명 방식이 만족스러울지 모르지만 아마 대부분의 독자들에게는 이 설명이 무슨 마법 주문처럼 들릴 것이다. 적어도 필자가 처음 이 설명을 들었을 때는 확실히 그랬다.
위 상황을 이해하는 데에 있어서 필자가 좋아하는 다른 설명이 있다. 이 설명의 결론부터 말하면 그것은 스핀 공간에 자기 홀극이 존재한다는 것이다. 앞선 섹션에서 설명한 아하로노브-봄 효과의 실험 상황과 비슷하게 스핀을 한 바퀴 회전시킬 때 그 “회전 경로” 안에 자기 홀극이 존재하고 그 자기 홀극이 여분의 위상각을 야기한다는 것이다.
조금 더 구체적으로 설명을 하면 다음과 같다. 앞선 섹션에서 보였듯이 자기 홀극의 세기는 다음과 같이 양자화된다.
\(g=n\frac{\phi_0}{4\pi}\)
이제 이 자기 홀극을 중심에 두고 주변을 한 바퀴 회전하는 입자가 얻게 될 위상각을 계산해 보자. 이 위상각은 아하로노브-봄 효과에서 설명했듯이 입자의 궤적 안에 갇힌 자속의 양에 비례한다. 그리고 이 자속의 양은 반구의 표면적 \(2\pi r^2\) (\(r\)은 구의 반지름)을 뚫고 지나가는 자기장의 총량이므로 다음과 같이 계산된다.
\(\Phi=2\pi r^2 \times \frac{g}{r^2}=2\pi g=\frac{n}{2}\phi_0\)
\(\Delta \phi=2\pi \Phi/\phi_0=n\pi\)
이 경우에 파동 함수에 최종적으로 곱해지는 위상 인자phase factor는 \(e^{i\Delta \phi}=e^{i n\pi}\)가 된다. 만약에 주어진 자기 홀극의 세기가 \(n=1\)의 경우에 해당한다면 자기 홀극에 의해서 야기되는 위상 인자는 \(-1\)이 될 수 있다는 것이다. 결론적으로 스핀 회전에 관한 필자의 설명이 맞는다면 스핀 공간에 그 세기가 \(g=\phi_0/4\pi\)인 자기 홀극이 존재해야 한다. 과연 그럴까?
예상했겠지만 답은 “그렇다”이다. 그런데 양자역학의 역사를 놓고 보면 이 답에 이르기까지 생각보다 매우 오랜 시간이 걸렸다. 양자 역학의 정립 이후에도 오랜 기간 동안 물리학자들은 파동 함수에서 위상각의 중요성을 제대로 깨닫지 못하고 있었다. 그 중요성을 처음 깨닫고 설파한 사람이 있었으니 그 사람은 바로 마이클 베리Michael Berry였다.
베리 위상
마이클 베리가 나중에 자신의 이름이 붙을 “베리 위상Berry phase”이라는 개념을 정립한 논문을 출간한 해는 1984년이다. 논문의 제목은 “단열적 변화에 수반하는 양자역학적 위상 인자Quantum phase factors accompanying adiabatic changes”이다. 이 수수께끼와 같은 제목을 가진 논문이 1984년에 출간되었다는 사실은 가만히 생각해 보면 매우 이상하다. 지금까지 “믿기 힘든 양자” 시리즈를 읽고 있는 독자들이 잘 알고 있듯이, 양자역학은 이미 1920년대 후반에 현재 우리가 알고 있는 형태 거의 그대로 정립되었다. 따라서 1980년대에 이르러서 양자역학에서 위상 인자 혹은 위상각의 효과가 재조명되었다는 사실은 매우 놀랍다. 다시 한번 위상의 귀환이다!
여기서 잠시 양자역학이 정립되던 1920년대 후반으로 돌아가 보자. 1926년 슈뢰딩거 방정식이 정립되자 많은 물리학자들은 슈뢰딩거 방정식을 이용해서 다양한 문제를 풀려고 노력했다. 하지만 물리학자들은 이내 슈뢰딩거 방정식을 정확하게 푸는 것이 생각보다 쉽지 않다는 사실을 깨닫는다. 이에 아주 정확하지는 않지만 특정한 조건 하에서는 정답에 충분히 가까운 답을 주는 다양한 근사approximation 방법이 개발되게 된다.
특히, 해밀토니안Hamiltonian이 시간에 따라서 변하는 문제는 정확한 답을 얻기에 가장 어려운 문제 중의 하나이다. 이 문제를 근사적이라도 풀기 위해서 1928년 막스 보른Max Born과 블라디미르 포크Vladimir Fock는 해밀토니안이 시간에 따라서 아주 천천히 변한다면 마치 시간이 멈춰진 상태에서 해밀토니안을 매 시각마다 대각화diagonalization하는 것이 충분히 좋은 근사 방법이 될 것이라고 추정하게 된다. 이 근사 방법은 이후 “단열 근사adiabatic approximation”라는 이름으로 알려지게 된다. 다시 말해서, 시간에 따라서 아주 천천히 변하는 슈뢰딩거 방정식의 해는 기본적으로 매 시각마다 얻어지는 해밀토니안의 “순간 고유상태instantaneous eigenstate”이다.
이제 해밀토니안이 시간에 따라서 아주 천천히 주기적으로 변하는 상황을 생각해 보자. 다시 말해서 어떤 긴 시간 주기가 지나고 나면 해밀토니안이 원래대로 되돌아가는 상황을 생각해 보자. 이 상황에서 보른과 포크의 단열 근사를 사용하면 파동 함수도 동일한 시간 주기가 지나면 원래의 파동 함수로 되돌아가야 한다. 왜 그렇지 않겠는가? 그렇지 않다고 의심할 이유는 전혀 없다. 적어도 상당히 오랜 기간 동안, 즉 베리가 나타나기 전까지 물리학자들은 그렇게 생각했다.
베리는 해밀토니안이 원래대로 되돌아가더라도 파동 함수는 반드시 원래의 파동 함수로 되돌아갈 필요가 없다고 생각했다. 원칙적으로 파동 함수는 임의의 위상 인자를 가질 수 있다. 이 위상 인자가 바로 베리 위상을 변수로 가지는 위상 인자이다. 어디선가 들어 본듯한 느낌이 들지 않는가? 앞선 섹션에서 필자가 설명하기를 전자의 스핀을 한 바퀴 돌리면 원래의 파동 함수에 여분의 마이너스 부호가 붙는다고 했다. 이 여분의 마이너스 부호가 위상각을 \(\pi\)로 가지는 위상 인자일 수 있다. 즉, \(-1=e^{i\pi}\)일 수 있다. 물론 진짜 이런 이유로 마이너스 부호가 붙었는지 아직 모른다. 확신을 갖기 위해서 베리의 유도 과정을 따라가 보자.
어떤 시스템을 기술하는 해밀토니안이 하나 있다고 하자. 이 해밀토니안은 어떤 매개변수parameter에 의존하는데, 이 매개변수는 시간에 따라 매우 천천히 변하는 물리량을 기술한다. 편의상 이 매개변수가 3개의 성분을 가지고 있어서 3차원 벡터로 표현될 수 있다고 하자. 수학적으로 쓰면 다음과 같다.
\(\hat{H}=\hat{H}({\bf R})\)
이제 주어진 \({\bf R}\) 값에서의 순간 고유상태를 \(|{\bf R}\rangle\)이라고 표기하자. 엄밀하게 말해서 주어진 \({\bf R}\) 값에서의 순간 고유상태는 하나가 아니라 여러 개 존재할 수 있다. 편의상 위에서 언급된 \(|{\bf R}\rangle\)이 \(n\) 번째 순간 고유상태라고 하자.
우리의 목표는 이 \(n\) 번째 순간 고유상태 \(|{\bf R}\rangle\)이 \({\bf R}\)의 함수로 어떻게 변하는지를 아는 것이다. 물론 실제로 해밀토니안을 풀면 순간 고유상태 \(|{\bf R}\rangle\)이 구체적으로 \({\bf R}\)의 어떤 함수인지를 알 수 있을 것이다. 그런데 우리의 진짜 목표는 순간 고유상태의 구체적인 함수 형태를 아는 것이 아니다. 아래 논의에서 차차 드러나겠지만, 우리의 진짜 궁극적인 목표는 순간 고유상태가 존재하는 매개변수 공간이 지니는 어떤 “변하지 않는 구조”를 찾는 것이다. 이 변하지 않는 구조는 소위 “위상학적 구조topological structure”이다. 앞선 섹션에서 논의한 내용을 바탕으로 풀어서 다시 말하면 이 구조는 “매개변수 공간에 자기 홀극이 있느냐 없느냐?”에 따라서 결정된다.
여기서 잠깐 여담 하나. 우리는 지금 파동 함수에서 위상의 중요성에 대해서 알아보고 있다. 여기서 위상은 영어로 “phase”이다. 이 “phase”라는 단어는 달의 위상이 초승달, 보름달, 그믐달로 바뀌는 것과 같이 한 주기를 지나면서 바뀌는 그 어떤 것의 “위치와 상태”를 의미한다. 위상각이 원점에서 복소 평면 위의 한 점 사이의 각도를 나타내는 것도 비슷한 의미이다. 그런데 위에서 “위상학적 구조”라는 단어에 나오는 위상은 영어로 “topology”이다. 이 “topology”라는 단어는 위상수학에서 다루는 위상이다. 위상수학은 어떤 기하학적인 물체에 구멍을 내거나 자르는 것과 같은 심각한 변형을 가하지 않을 때 변하지 않고 유지되는 수학적인 양에 관심을 두는 기하학의 한 분야이다. “phase”로서의 위상과 “topology”로서의 위상은 영어로는 구분되나 한국어 혹은 한자로는 동일한 단어이다. 여기서 한국 사람으로서 깨달을 수 있는 재미있는 우연의 일치가 하나 있다. 그것은 “phase”로서의 위상과 “topology”로서의 위상이 양자역학의 세계에서 서로 긴밀하게 연결된다는 것이다. 참으로 묘한 우연의 일치가 아닐 수 없다.
이제 여담을 마치고 다시 우리가 당면한 목표로 돌아가 보자. 다시 말해서, 순간 고유상태 \(|{\bf R}\rangle\)이 \({\bf R}\)의 함수로 어떻게 변하는지 계산해 보자. 그러기 위해서 \({\bf R}\)이 \({\bf R}+\Delta {\bf R}\)로 약간 변한 후에 얻어지는 순간 고유상태인 \(|{\bf R}+\Delta {\bf R}\rangle\)과 기존의 순간 고유상태인 \(|{\bf R}\rangle\) 사이에 내적inner product을 취해 보자.
\(\langle {\bf R} |{\bf R}+\Delta {\bf R}\rangle\)
여기서 중요한 가정은 \(|{\bf R}+\Delta {\bf R}\rangle\)도 주어진 값 \({\bf R}+\Delta {\bf R}\)에서 \(n\) 번째 순간 고유상태라는 것이다. 이 가정은 다름이 아니라 단열 근사인데, \({\bf R}\) 값이 시간에 따라 아주 천천히 변하기 때문에 순간 고유상태들의 순서가 바꾸지 않는다는 가정이다.
이제 \(\Delta {\bf R}\)이 작다는 가정하에 \(|{\bf R}+\Delta {\bf R}\rangle\)을 테일러 전개Taylor expansion해서 위 수식에 집어넣으면 다음과 같은 결과를 얻을 수 있다.
\(\langle {\bf R} |{\bf R}+\Delta {\bf R}\rangle \simeq 1 + \langle {\bf R}| \nabla_{\bf R}|{\bf R}\rangle \cdot \Delta {\bf R}\)
위에서 \(\nabla_{\bf R}\)은 \({\bf R}\)에 대해서 미분을 취한다는 것을 의미한다. 위 수식은 다시 한번 \(\Delta {\bf R}\)이 작다는 가정하에 지수 함수의 형태로 바꾸어 쓸 수 있다.
\(\langle {\bf R} |{\bf R}+\Delta {\bf R}\rangle \simeq e^{ i {\cal A}_{\bf R} \cdot \Delta {\bf R}}\)
여기서 \({\cal A}_{\bf R}\)은 다음과 같이 정의된다.
\({\cal A}_{\bf R}=-i\langle{\bf R}|\nabla_{\bf R}|{\bf R}\rangle\)
자, 이제 \({\bf R}\)을 위와 같이 조금씩 바꾸어 가면서 매개변수 공간에서 어떤 궤적을 따라간다고 하자. 특히, 궤적이 폐곡선을 형성해서 \({\bf R}\)이 원래 시작한 값으로 돌아온다고 하자. 이러한 과정을 통해서 얻어지는 최종적인 위상 인자는 다름 아니라 \({\bf R}\)을 조금씩 변할 때마다 각 단계에서 얻어지는 위상 인자를 모두 다 곱한 값과 같다.
\(e^{i\oint{\cal A}_{\bf R}\cdot d {\bf R}}\)
위 공식을 자세히 들여다보자. 무엇인가 기시감이 들지 않는가?
위 공식에 나오는 위상은 아하로노브-봄 효과를 설명할 때 벡터 퍼텐셜에 의해서 야기되는 위상과 매우 유사한 수학적 형태를 지닌다. 조금 더 엄밀하게 말해서, 자속 양자의 단위인 \(\phi_0/2\pi\)를 1로 치환할 때 위 공식에 나오는 위상은 아하로노브-봄 효과를 주는 위상과 수학적으로 완전히 동일하다. 이제 이러한 수학적 유사성에 영감을 받아서 \({\cal A}_{\bf R}\)이 아예 매개변수 공간에서 정의된 “유효 벡터 퍼텐셜effective vector potential”이라고 상상해 보자. 그리고 \({\cal A}_{\bf R}\)에 컬 미분을 취하면 매개변수 공간에 존재하는 “유효 자기장effective magnetic field”이 얻어진다고 상상해 보자.
\({\cal B}_{\bf R}=\nabla_{\bf R}\times{\cal A}_{\bf R}\)
참고로 \({\cal A}_{\bf R}\)은 전문적인 용어로 “베리 연결Berry connection”이라고 부르고, \({\cal B}_{\bf R}\)은 “베리 곡률Berry curvature”이라고 부른다. 그런데 이러한 상상이 과연 말이 되는 것일까?
밀이 되는지 알아보기 위해서 구체적인 해밀토니안을 하나 생각해 보자.
\(\hat{H}=-{\bf R}\cdot \sigma=-(R_x \sigma_x +R_y \sigma_y +R_z \sigma_z)\)
이 해밀토니안은 스핀의 동역학을 기술하는 가장 간단한 해밀토니안이다. 이 해밀토니안은 매개변수 벡터 \({\bf R}\)의 방향으로 스핀을 정렬시킨다. 왜 그럴까? 우선, 이 해밀토니안은 \(2\times 2\) 행렬로 주어지기 때문에 그것의 고유상태eigenstate는 단 두 개이다. 이 두 개의 고유상태는 각각 \({\bf R}\)의 순방향과 역방향으로 스핀이 정렬되는 상태이다. 그들의 에너지 고유값energy eigenvalue은 각각 \(-R\)과 \(R\)로 주어진다. 여기서 \(R\)은 \({\bf R}\) 벡터의 크기로 \(\sqrt{R^2_x+R^2_y+R^2_z}\)이다. 결론적으로 \({\bf R}\)의 순방향으로 스핀이 정렬되는 상태는 바닥 상태ground state가 되고, 역방향으로 스핀이 정렬되는 상태는 여기 상태excited state가 된다. 참고로 위 해밀토니안은 처음 고안한 물리학자 피에터 제만Pieter Zeeman의 이름을 따서 “제만 해밀토니안”이라고 불린다.
이제 위 해밀토니안에 대해서 매개변수 공간에 존재하는 유효 자기장, 즉 베리 곡률을 계산해 보자. 여기서 자세한 유도 과정을 보여줄 수는 없으나 차근차근 계산하면 바닥 상태의 베리 곡률은 다음과 같다는 결론을 얻을 수 있다.
\({\cal B}_{\bf R}=\frac{g}{R^2}\hat{\bf R}\)
이 공식은 자기 홀극으로부터 방사 방향으로 뿜어져 나오는 자기장을 기술하는 바로 그 공식과 정확히 같다. 특히, 여기서 주목해야 할 사실은 위에서 자기 홀극의 세기가 \(g=1/2\)이라는 것이다. 이 값은 앞에서 자속 양자의 단위가 재정의된 것을 고려하면 스핀을 360도 회전시킬 때 생기는 마이너스 부호를 위해서 꼭 필요했던 바로 그 값, \(g=\phi_0/4\pi\)와 정확히 같다! (참고로 여기 상태의 베리 곡률은 위와 정확히 같은 공식에 \(g\)의 부호만 바꾸면 된다.) 이제 드디어 우리가 그동안 그렇게 얻고 싶었던 결론에 도달했다. 그것은 스핀 공간에 자기 홀극이 존재한다는 것이다.
이제까지 설명한 내용만으로도 위상의 귀환은 그동안 충분히 흥미로운 역사를 써 내려왔다. 그런데 위상은 최근에 다시 한번 더 아름답게 귀환했다. 이번 귀환은 “위상 절연체topological insulator”라는 특별한 이름을 지닌 물질 상태를 통해서 이루어졌다.
위상 절연체
물질의 상태를 제대로 이해하기 위해서는 지금까지 필자가 “믿기 힘든 양자” 시리즈를 통해서 설명한 내용으로는 아직 부족하다. 사실 모든 물질은 궁극적으로 양자역학이 없이는 이해될 수 없다. 따라서 엄밀하게 말하면 모든 물질의 상태는 양자 물질 상태이다. 양자 물질 상태에 대한 자세한 내용은 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 설명할 예정이니 관심 있는 독자들은 조금만 기다려 주기를 부탁한다. 다만 여기서는 위상 절연체라는 물질 상태를 이해하기 위해서 필요한 응집물질물리condensed matter physics에 관한 기본적인 두 가지 사실만을 설명하기로 한다.
우선 첫 번째로 알아야 할 사실은 입자의 통계statistics이다. 기억을 되살려 보면 지금까지 우리가 고려한 파동 함수는 주로 단일 입자의 동역학을 기술했다. “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 입자가 여러 개인 경우에 적용 가능한 슈뢰딩거 방정식을 쓰기는 했지만 그것의 해로 얻어지는 다중 입자를 위한 파동 함수가 구체적으로 어떻게 쓰여야 하는지에 대해서는 자세한 이야기를 하지 않았다.
입자가 단 하나 있는 경우와 여러 개 있는 경우에는 도대체 무슨 차이가 있을까? 당연히 입자가 단 하나 있으면 상호작용이 없고, 여러 개 있으면 입자들 사이에 상호 작용이 있다. 굉장히 큰 차이이다. 그런데 양자역학에서는 상호작용을 고려하기 전에 우선적으로 고려해야 하는 것이 있다. 그것은 바로 입자가 만족해야 하는 통계이다.
간단하게 말해서, 우주의 모든 입자는 페르미온fermion과 보존boson이라는 두 종류의 입자로 나뉜다. 이 두 종류의 입자는 서로 다른 통계 법칙을 따른다. 즉, 페르미온은 페르미-디랙 통계Fermi-Dirac statistics를 따르고, 보존은 보스-아인슈타인 통계Bose-Einstein statistics를 따른다. 자세한 내용은 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 설명하겠지만, 중요한 사실은 입자의 통계가 다중 입자를 위한 파동 함수, 줄여서 다체 파동 함수many-body wave function의 수학적 형태에 특정한 제한을 가한다는 것이다.
특히, 물질의 상태를 결정하는 데에 가장 중요한 역할을 하는 전자는 페르미온으로서 “파울리 배타 원리Pauli exclusion principle”를 만족한다. 다시 말해서, 전자는 하나의 상태에 반드시 하나의 전자만 들어갈 수 있다. 배타 원리라는 이름이 말해 주듯이 주어진 전자는 자기가 채우고 있는 상태에 다른 전자가 들어오는 것을 배타한다. 결론적으로 전자들은 서로 자기의 영역을 지키기 위해서 에너지가 낮은 상태부터 높은 상태로 차곡차곡 양자 상태를 채워나가게 된다. 비유적으로 말해서 그릇에 부어지는 물이 바닥부터 차곡차곡 차오르는 것과 같다.
응집물질물리에 관해서 알아야 할 두 번째 사실은 주기적인 격자lattice 구조를 가지는 고체 속에서 전자의 운동 에너지에 생기는 변화이다. 우리가 잘 알고 있듯이 전자가 진공 속에서 움직일 때 운동 에너지는 다음과 같이 주어진다.
\(T=\frac{p^2}{2m}=\frac{\hbar^2}{2m}k^2\)
즉, 운동 에너지는 운동량, 즉 파수 \(k\)의 제곱에 비례한다. 여기서 \(m\)은 물론 전자의 질량이다. 하지만 전자가 주기적인 격자 구조를 형성하고 있는 고체 속에서 움직일 때 운동 에너지는 위와 같이 단순하지 않다.
우선 격자 속에서 파수는 진공 속에서와 다르게 무한히 커질 수 없다. 그 이유는 격자를 이루는 원자 사이의 거리 \(a\)보다 짧은 파장을 가지는 파동은 물리적으로 의미가 없기 때문이다. 수학적으로 말해서 격자 속에 존재하는 파동의 파수는 0부터 시작해서 최대 \(2\pi/a\)까지의 값만을 가질 수 있다. 사실은 엄밀하게 말해서 파수는 이 영역을 넘어서는 값을 가질 수 있다. 다만, 파수가 이 영역을 넘어서더라도 운동 에너지는 정확히 반복되어 물리적으로 아무런 차이가 없어지게 된다. 즉, 격자 속에서 움직이는 전자의 운동 에너지는 파수의 주기적인 함수periodic function가 된다. 따라서 파수가 물리적으로 의미 있는 영역은 편의에 따라서 0부터 \(2\pi/a\)까지, 혹은 \(-\pi/a\)부터 \(\pi/a\)까지, 혹은 그것도 아니면 \(2\pi/a\)의 길이를 가지는 그 어떤 범위가 되든지 마음대로 정할 수 있다. 참고로 이렇게 파수가 물리적으로 의미 있는 영역을 “브릴루앙 영역Brillouin zone”이라고 부른다. 결론적으로 격자 속 전자는 브릴루앙 영역에 속하는 파수만 가질 수 있다.
격자 속에서 생기는 또 다른 중요한 변화는 파동이 가질 수 있는 운동 에너지의 값에도 특정한 제한이 가해진다는 것이다. 다시 말해서, 격자 속에 존재하는 파동의 운동 에너지는 특정하게 허용되는 구간의 값만을 가질 수 있다. 참고로, 이렇게 허용되는 운동 에너지의 구간을 “에너지 띠energy band”라고 부른다. 에너지 띠와 관련해서 우리가 특별히 관심을 가지는 상황이 있다. 그것은 에너지 띠들이 띄엄띄엄 떨어져 존재하는 상황이다. 이러한 에너지 띠들 사이의 간격을 “에너지 간격energy gap”이라고 부른다.
양자 물질 상태에 관한 다른 자세한 내용과 마찬가지로 에너지 띠와 에너지 간격이 형성되는 이유도 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 자세하게 설명할 예정이다. 이렇게 자세한 설명은 나중으로 미룰 수밖에 없지만, 여기서는 비유일지라도 직관을 갖는 것이 중요하다. 비유적으로 말해서, 전자가 고체 속에 띄엄띄엄 존재하는 에너지 띠를 통해서만 움직일 수 있는 것은 마치 지하수의 물줄기가 땅속에 띄엄띄엄 존재하는 빈 공간을 통해서만 흐를 수 있는 것과 비슷하다.
이제 위에서 설명한 응집물질물리에 관한 두 가지 사실을 결합하면 다음과 같은 결론에 도달한다. 고체 속에 존재하는 전자들은 에너지가 낮은 에너지 띠부터 차곡차곡 채우면서 최상위 에너지 띠까지 도달한다. 이때 각각의 에너지 띠에 들어갈 수 있는 전자의 총 개수는 브릴루앙 영역에 존재하는 파수의 개수와 같다. 전자로 최상위 에너지 띠를 채우는 방법에는 두 가지 경우가 있다. 우선 최상위 에너지 띠가 완벽하게 전자로 가득 차는 경우이다. 이때 고체는 전기가 잘 통하지 않는 절연체insulator가 된다. 에너지 간격이 그렇게 크지 않는 경우에는 전기가 반쯤 통하는 반도체semiconductor가 되기도 한다. 전기가 통하지 않는 이유는 전자가 움직이려면 빈 있는 공간이 있어야 하는데 이미 전자들이 모든 자리를 채우고 있어서 전혀 움직일 수 없기 때문이다. 반면에 최상위 에너지 띠가 완벽하게 전자로 가득 차지 않고 적절하게 빈 있는 공간이 있다면 이 고체는 도체conductor 혹은 금속metal이 된다.
이제 지금까지 배운 지식을 가지고 위상 절연체를 정의해 보자. 간단하게 말해서, 위상 절연체란 최상위 에너지 띠가 위상학적인 성질을 지니는 절연체이다. 그렇다면 에너지 띠가 위상학적인 성질을 지닌다는 것은 무슨 의미인가? 이 질문에 대한 답은 우리를 다시 자기 홀극이 존재하는 스핀 공간으로 이끈다.
구체적인 예를 통해서 도대체 이 말이 무슨 의미인지 이해해 보자. 편의상 우리의 고체가 2차원에 존재한다고 하자. 그리고 [그림7]에서 보는 것과 같이 어떤 두 에너지 띠가 브릴루앙 영역의 한 구간에서 서로 가깝게 접근한다고 상상해 보자.
이 경우에 두 에너지 띠를 기술하는 해밀토니안은 일반적으로 다음과 같이 쓸 수 있다.
\(\hat{H}=-{\bf R}(k_x,k_y)\cdot \sigma\)
여기서 3차원 매개변수 벡터 \({\bf R}\)은 2차원 파수 벡터 \((k_x,k_y)\)의 함수이다. 어디선가 본 익숙한 해밀토니안이다. 이 해밀토니안은 스핀의 동역학을 기술하는 제만 해밀토니안과 정확하게 같다!
이제 앞선 섹션에서 배운 사실을 하나 기억해 보자. 그것은 매개변수 \({\bf R}\)로 표현되는 스핀 공간에 자기 홀극이 존재한다는 것이다. 구체적으로, \({\bf R}=0\)인 원점에 자기 홀극이 존재한다. 그런데 위에서 말했듯이 매개변수 \({\bf R}\)은 파수 벡터 \((k_x,k_y)\)의 함수이므로 각각의 파수 벡터마다 그것에 해당하는 \({\bf R}\)이 하나씩 대응된다. 이제 최상위 에너지 띠에 올려진 전자들이 브릴루앙 영역에 속하는 모든 평면파 상태들을 차곡차곡 빠짐없이 꽉 채운다고 하자. 그렇게 되면 꽉 채워진 브릴루앙 영역에 대응해서 \({\bf R}\)도 스핀 매개변수 공간에서 어떤 곡면surface을 형성할 것이다. 이 곡면이 원점에 있는 자기 홀극을 품는다면 이 상태는 위상 절연체가 된다.
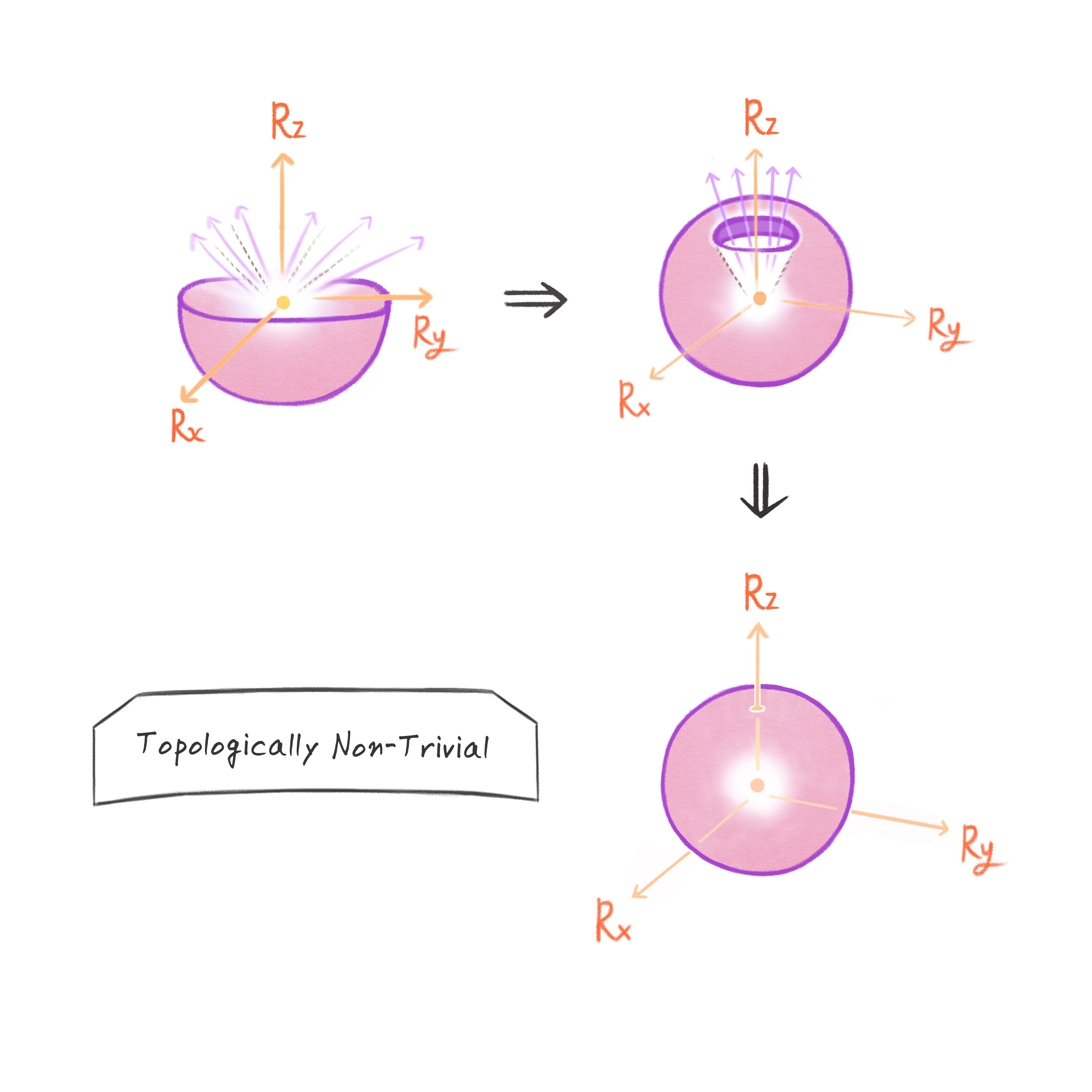
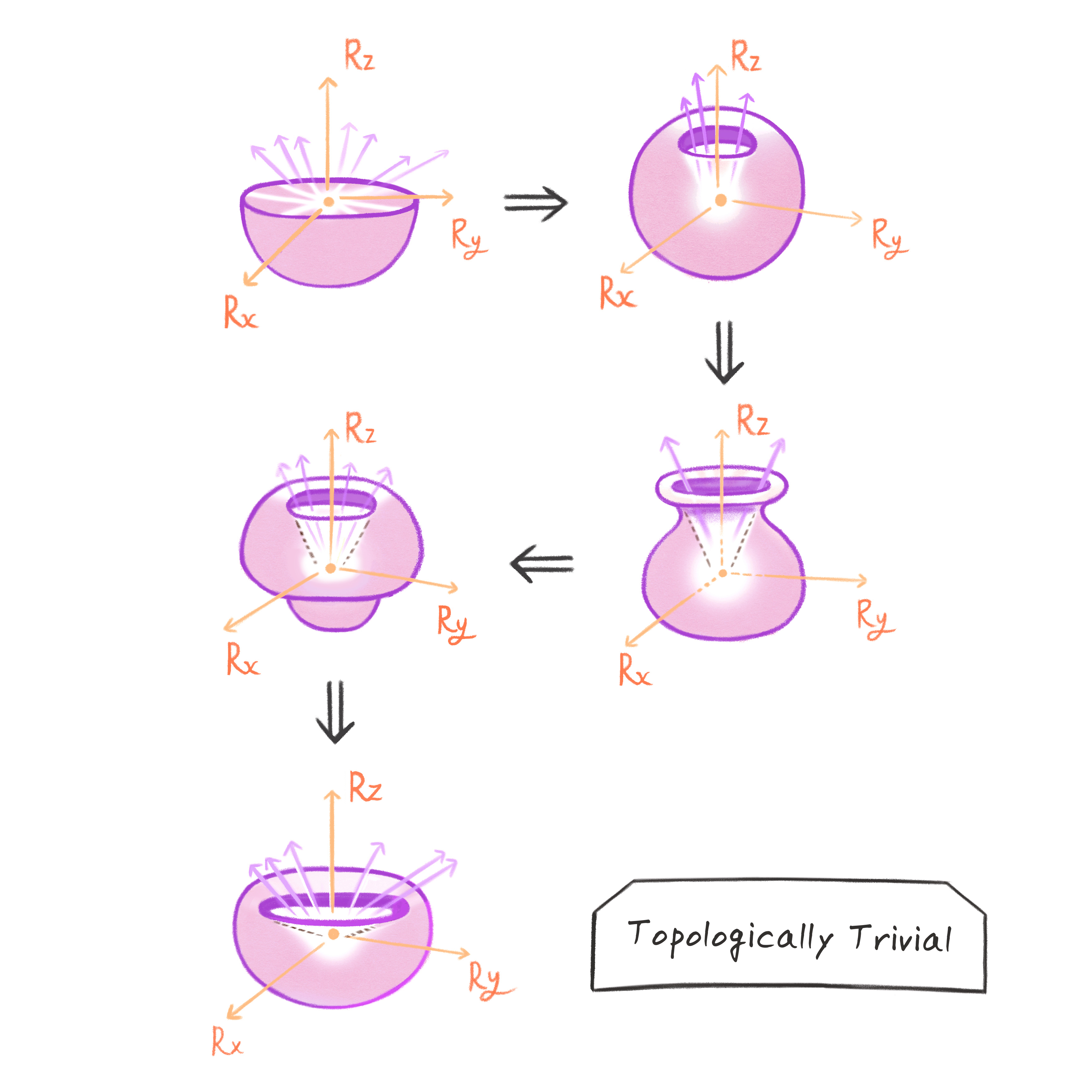
논의가 조금 복잡하니까 우화를 통해서 다시 한번 이해해 보도록 하자. 브릴루앙 영역을 신축성이 좋은 보자기로 생각해 보자. 이 보자기는 전자라는 구슬로 촘촘히 장식이 되어있다. 전자는 파울리 배타 원리로 인해서 한 곳에 한 개 이상 박아 넣을 수는 없다. 이제 이 보자기로 자기 홀극이라는 빛나는 보석을 감싸고 싶다고 하자. 완전히 감싸서 보석의 빛을 모두 가릴 수 있다면 성공이다. 이 성공한 상태가 바로 위상학적으로 뻔하지 않은topologically nontrivial 절연체, 즉 위상 절연체이다. 반면에 완전히 감싸지 못해서 빛이 새어 나갈 수 있다면 위상학적으로 뻔한topologically trivial 절연체, 즉 보통의 절연체이다. 참고로 [그림8]과 [그림9]는 각각 위상학적으로 뻔하지 않은 상황과 뻔한 상황을 시각적으로 표현한 것이다.
정리해 보자. 절연체는 두 종류로 나뉘다. 위상학적으로 뻔하지 않은 절연체와 뻔한 절연체가 바로 그 두 종류이다. 위상학적으로 뻔하지 않은 절연체, 즉 위상 절연체는 최상위 에너지 띠가 매개변수 공간에 존재하는 자기 홀극을 그 안에 감싸고 있는 절연체이다. 반면에 위상학적으로 뻔한 절연체는 그렇지 않은 절연체이다. 눈에 보이지 않는 가공의 공간에 존재하는 자기 홀극이 물질의 상태를 구분할 수 있다니, 무엇인가 대단히 멋진 느낌이 든다. 하지만 멋을 떠나서 도대체 이 모든 것은 무엇을 의미하는 것일까? 두 종류로 구분되는 절연체는 실제로 어떻게 다른 것일까? 이 질문에 대해서 여러 가지 답이 있을 수 있지만 여기서는 실험적으로 중요하고 직관적으로 가장 이해하기 쉬운 답 하나에 대해서 짧게 설명하고자 한다.
우선 앞서 말했듯이 절연체는 전기가 잘 통하지 않는 고체 상태의 물질이다. 어찌 보면 당연한 것 같지만 보통의 절연체, 즉 위상학적으로 뻔한 절연체는 고체 내부는 물론 표면으로도 전기가 잘 흐르지 않는다. 반면에 위상 절연체는 이상하게 고체 내부로는 전기가 잘 흐르지 않지만 표면으로는 잘 흐를 수 있다. 이 이상한 성질의 이유는 다음과 같다.
어떤 위상 절연체가 진공 속에 놓여 있다고 하자. 진공은 언뜻 생각하면 절연체가 아닌 것 같지만 우리의 우주에 자유롭게 흘러 다니는 전자가 거의 없다는 사실을 생각하면 절연체와 다름없다. 그리고 진공은 위상학적으로 뻔하다. 따라서 위상 절연체의 표면은 위상학적으로 뻔하지 않은 절연체인 그 자신과 위상학적으로 뻔한 절연체인 진공 사이의 접합면이다. 이런 상황에서 전자는 각각의 절연체가 가지는 위상학적인 성질을 부드럽게 연결할 수 없다. 앞선 보자기 우화를 빌려서 설명하면, 위상 절연체 속에서 자기 홀극을 감싸고 있던 보자기가 감싸지 않고 있는 진공으로 넘어가기 위해서는 보자기가 찢어지든지 구멍이 나야 한다. 이렇게 큰 위상학적인 변화는 접합면에서 절연체라는 성질이 붕괴하는 것을 의미한다. 결과적으로 전자는 위상 절연체의 표면에서 자유롭게 움직여 다닐 수 있다.
주어진 시간에 무엇을 할 것인가
이번 글을 통해서 필자는 파동 함수의 위상이 어떻게 반복해서 현대 물리학 연구의 중심으로 귀환해 왔는지 설명했다. 지금까지 연재 글을 꾸준히 읽어 오고 있는 독자들은 잘 알겠지만 필자가 “믿기 힘든 양자” 시리즈를 통해서 가장 강조하고 싶은 내용 중의 하나는 파동 함수가 복소수라는 사실이다. 그리고 파동 함수가 복소수라는 사실을 가장 극적으로 나타내는 성질은 바로 위상의 존재이다.
위상은 영의 이중 슬릿 실험에서 무심하게 그 존재를 드러내기 시작하여 아하로노브-봄 효과에서 이르러 우리에게 물리적으로 실제로 잴 수 있는 것은 과연 무엇인가라는 심오한 질문을 던졌다. 그리고 위상은 디랙으로 하여금 자기 홀극이 만약에 전 우주에 단 하나라도 존재한다면 우주에 존재하는 모든 입자의 전기 전하는 양자화되어야 한다는 장대한 결론에 도달하게 만들었다.
자기 홀극은 아직까지 실공간에 존재하는 입자로 발견되지 않았다. 하지만 놀랍게도 자기 홀극은 이미 스핀 공간에 존재하고 있었다. 스핀을 360도 돌리면 파동 함수가 자기 자신으로 돌아오지 않고 \(-1\)이라는 위상 인자가 붙는 기이한 현상은 스핀 공간에 자기 홀극이 존재하고 있다는 사실을 암시하고 있었다. 하지만 이 사실은 오랫동안 큰 관심을 받지 못 했다. 양자역학이 정립된 후 한참이 지난 1984년, 베리는 파동 함수의 위상이 위상학적인 성질을 가지게 되면 실험적으로 잴 수 있는 효과를 가져올 수 있다는 놀라운 이론을 펴게 된다. 이 이론은 이후에 베리 위상이라는 개념으로 정리된다.
그리고 이 베리 위상은 응집물질 물리학자들로 하여금 위상학적으로 뻔하지 않은 절연체, 즉 위상 절연체라는 새로운 물질 상태를 상상하게 만들었다. 이렇게 상상하게 된 위상 절연체는 최근에 실제로 실험적으로 발견되었고, 이로 인해서 위상은 다시 한번 현대 물리학 연구의 중심으로 화려하게 귀환하게 된다.
이 글을 쓰고 있는 지금, 필자는 미국 보스턴Boston에서 안식년sabbatical을 보내고 있다. “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 언급하였듯 필자는 1995년에 박사 학위 과정을 밟기 위해서 미국에 도착했다. 이후 2000년에 박사 학위를 받고 두 번의 박사후 연구원postdoctoral researcher 과정을 거쳐서 2005년에 한국으로 귀국했다. 그리고 필자는 그로부터 14년이 지난 2019년 3월 미국으로 귀환했다. 그동안 많은 것이 변했고 필자도 늙었다. 하지만 마음만은 박사 학위를 받은 지 얼마 안 되는 어린 물리학자로 되돌아간 것 같다. “위상의 귀환”이라는 글을 쓰고 있는 이 순간, 필자가 어린 물리학자였던 시절로 귀환한 느낌을 받고 있는 것이 묘하다.
본래 안식년이라는 것의 취지가 그러하거니와 필자에게는 지금 숨 가쁘게 달려온 지난날을 되돌아볼 수 있는 시간이 주어졌다. 주어진 시간에 무엇을 할 것인가? 일단 연구에 관해서는 필자의 전공 분야인 위상 물질topological matter에서 위상phase이 하는 근본적인 역할에 대해서 깊게 고민해 보고 싶다. 그리고 이 고민이 앞으로 있을 또 다른 위상의 귀환을 가져올 수 있기를 바라본다.
일 년 뒤에 이어질 또 다른 귀환, 한국으로의 귀환을 고대하며…