데이터의 정보기하학: 통계학적인 학습

주어진 데이터를 설명하는 최소한의 모형은 어떤 모습일까?

앞선 세 번의 연재에서는 그래프 기반의 신경망 모형을 소개하고, 정보이론을 통해서 이들의 학습과정을 살펴보았다. 이번 글에서는 모형으로부터 자유로운 통계학적인 학습을 살펴보겠다.

$L$ 개의 관찰 데이터 $\{x(t)\}_{t=1}^L$ 가 주어졌다고 하자. 이런 데이터를 생성하는 시스템이 가지는 가장 그럴듯한 분포 $P(x)$ 는 어떤 모습일까? 아마도 우리가 상상할 수 있는 가장 원시적인 분포는 주어진 데이터의 빈도수일 것이다.

$\begin{equation} \tag{1} P_0(x=\underline{x}) = \frac{1}{L} \sum_{t=1}^L \delta(\underline{x} – x(t))\end{equation}$
이는 데이터

$\{x(t)\}_{t=1}^L$ 가운데

$\underline{x}$ 에 해당하는 것이 몇 개인지 세는 상대적인 빈도수를 나타내는 표현이다. 그리고 주어진 데이터의 통계량인 평균을 살펴볼 것이다.

$\begin{equation} \tag{2} X_0 = \frac{1}{L} \sum_{t=1}^L x(t) = \sum_x x P_0(x) \end{equation}$

우리가 찾고 있는 시스템의 모분포 $P(x)$ 는 가능하면 $P_0(x)$ 에 가깝고 평균 $X=\sum_x x P(x)$ 는 $X_0$ 에 가까운 값을 주는 분포로 기대가 된다.

여기서 한 걸음 더 나가려면 두 확률분포 사이의 거리를 정의해야 한다. 여러 가능성 가운데 쿨백-라이블러 발산^{Kullback-Leibler divergence}를 생각해보자.

$\begin{equation} \tag{3} D_{KL} (P||P_0) = \sum_x P(x) \log \frac{P(x)}{P_0(x)} \end{equation}$
이렇게 정의한 거리

$D_{KL} (P||P_0) \geq 0$ 는 일단 항상 양수이고,

$P(x)=P_0(x)$ 가 되는 조건에서만 거리가

$0$ 이 되므로 꽤 괜찮은 선택처럼 보인다. 사실은 최고의 선택이다. 공간에서 두 점 사이의 거리를 다루는 리만기하학을 일반화해서 함수공간에서 두 분포함수 사이의 거리를 다루는 정보기하학^{information geometry}이라는 분야가 있다. 정보기하학에 따르면

$D_{KL}(P||P_0)$ 로 정의한 거리는 (i)

$x$ 의 해상도^binning에 의존하지 않고, (ii) 일반적인 의미에서의 피타고라스 정리를 만족하는 유일한 선택이다.[1] 정보기하학은 슌이치 아마리^{Shun-ichi Amari} 선생님을 비롯한 분들의 꾸준한 기여로 최근 머신러닝을 이해하는 언어로 주목받고 있다.[2]

^영상 아마리 선생님의 유튜브영상

쿨백-라이블러 발산을 조금 정리하면 다음처럼 표현할 수 있다.

$\begin{align} D_{KL} (P||P_0) &= \sum_x P(x) \log \frac{1}{P_0(x)} – \sum_x P(x) \log \frac{1}{P(x)} \nonumber \\ &= \mathbb{E} \bigg[\log \frac{1}{P_0(x)} \bigg]_P – \mathbb{E} \bigg[\log \frac{1}{P(x)} \bigg]_P \tag{4} \end{align}$
이는

$P_0(x)$ 분포가 가지는 정보의 기대값에서

$P(x)$ 분포가 가지는 정보의 기대값의 차이에 해당한다. 이런 의미에서 쿨백-라이블러 발산은 상대적 엔트로피^{relative entropy}라고도 불린다. 여기서 두 정보량의 기대값 계산에서 모두 정답에 해당하는 모분포

$P(x)$ 의 입장에서 계산했다는 점을 주목하자. 이렇게 보면 거리함수

$D_{KL}(P||P_0) \neq D_{KL}(P_0||P)$ 가

$P(x)$ 와

$P_0(x)$ 에 대해 대칭이 아니라는 것이 실수가 아니라 신의 한 수임을 자연스럽게 이해할 수 있다. 이제 거리함수

$D_{KL}(P||P_0)$ 를 이용해서 우리 문제를 형식화해보자.

$\sum_x x P(x) = X$ 를 만족하면서 $P_0(x)$ 에 가까운 분포 $P(x)$ 는 무엇인가?

이렇게 제한 조건이 있는 최적화 문제는 라그랑주 승수법을 써서 푼다.

$\begin{equation} \tag{5} \mathcal{L} = D_{KL}(P||P_0) – \theta \cdot \bigg( \sum_x x P(x) – X \bigg) \end{equation}$
이 목적함수를 최소화시키는

$P(x)$ 를 계산하면 다음과 같은 지수함수를 얻게 된다.[3]

$\begin{equation} \tag{6} \label{eq:boltzmann} P(x) = \frac{P_0(x) \exp(\theta \cdot x)}{Z} \end{equation}$
분모

$Z=\sum_x P_0(x) \exp(\theta x)$ 는

$\sum_x P(x)=1$ 을 만족하기 위해 도입한 정규화 상수이다. 이 분포의 매개변수인 라그랑주 승수

$\theta$ 는 제한 조건

$\sum_x x P(x) = X$ 을 만족하도록 결정한다. 여기서

$X=X_0$ 인 제한 조건을 만족하는 경우는

$\theta=0$ 이 되고, 당연하게도

$P(x)=P_0(x)$ 라는 결론을 확인할 수 있다. 하지만 우리가 관심이 있는 상황은

$X$ 가

$X_0$ 에서 조금 벗어난 데이터에 대한

$P(x)$ 이다.

흥미로운 식 (6)을 몇 가지 상황에서 음미해 보자. 첫째, 데이터가 각 샘플의 상태 $x$ 자체가 아니라 이 상태에 해당하는 어떤 물리량 $E(x)$ 를 측정한 경우를 생각해 보자. 그리고 $P_0(x)$ 에 대한 정보가 아무것도 없어서 모든 상태 $x$ 가 같은 확률로 나타날 수 있는 상황을 가정해 보자. 그러면 측정한 $E(x)$ 의 평균 $U = \sum_x E(x) P(x)$ 가 제한된 조건에서 $P_0(x)$ =상수에 가장 가까운 분포를 얻으면 $P(x)=Z^{-1} \exp[-\beta E(x)]$ 라는 통계역학의 볼츠만 분포를 얻게 된다. 여기서 물리량 $E(x)$ 는 에너지에 해당하고, $\theta = -1/\beta$ 에 해당한다. 이 경우 $P(x)$ 는 $1/\beta$ 라는 온도에서 평균 에너지 $U$ 를 가지는 평형상태의 분포가 된다. 여기서 열역학에 기반을 둔 통계역학과 정보이론에 기반을 둔 데이터사이언스의 접점이 생긴다.

둘째, 제한조건이 두 개 있는 경우를 생각해 보자. $x$ 의 1차 모멘트 $\sum_x x P(x)$ 와 더불어 2차 모멘트 $\sum_x x^2 P(x)$ 도 제한조건으로 들어오는 경우는 $P(x) = Z^{-1} \exp(\theta_1 x + \theta_2 x^2)$ 가 정규분포 또는 가우시안분포가 된다.² 이는 평균과 분산을 측정한 실험결과를 설명하는 최소한의 모형으로 정규분포를 가정하는 것에 대한 정보이론적인 정당화이다.

셋째, $x = (x_1, x_2, \cdots)$ 가 2차원 이상의 벡터이고 관찰한 물리량이 $x_i$ 의 평균 그리고 상관관계로 불리는 $x_i x_j$ 의 평균이었다고 하면 $P(x) = Z^{-1} \exp(\sum_i b_i x_i + \sum_{i>j} W_{ij} x_i x_j)$ 와 같은 홉필드 모형을 자연스럽게 얻게 된다. 이 경우 라그랑주 승수는 $\theta = (b_i, W_{ij})$ 에 해당한다.

샛길로 빠졌는데, 다시 우리의 문제에서 얻은 식 (6)으로 돌아가자. 정규화 상수 $Z$ 는 통계역학에서는 분배함수^{partition function}로 불리고, $Z$ 에 로그를 취하면 적률생성함수 $F(\theta)=\log Z(\theta)$ 가 된다. 적률생성함수에 미분을 취하면 $x$ 의 모멘트의 기대값을 편리하게 얻을 수 있다. 가령, 1차 모멘트의 기대값은 $F(\theta)$ 를 $\theta$ 에 대해서 한 번 미분을 해서 다음과 같이 계산할 수 있다.

$\begin{align} \frac{\partial F(\theta)}{\partial \theta} &= \frac{1}{Z(\theta)}\frac{\partial Z(\theta)}{\partial \theta} \nonumber \\ &= \sum_x \frac{xP_0(x) \exp(\theta \cdot x)}{Z(\theta)} = \sum_x x P(x) = X \tag{7} \end{align}$
마찬가지로 고차 모멘트의 경우는

$\theta$ 에 대해 여러 번 미분을 해서 얻을 수 있다. 즉, 적률생성함수

$F(\theta)$ 는 확률분포

$P(x)$ 에 대한 모든 정보를 가지고 있다고 생각할 수 있다. 따라서 지금부터 우리는

$P(x)$ 대신

$F(\theta)$ 를 찾을 것이다.

여기서 이런 질문을 해보자. 데이터의 평균값 $X_0$ 가 조금 바뀌면 우리의 분포 $P(x)$ 는 어떻게 될까? 물론 라그랑주 승수인 $\theta$ 를 조정하면 $P(x)$ 와 평균값 $X$ 를 변화시킬 수 있다. 우리는 수학적인 도구로 도입한 $\theta$ 대신 데이터의 평균 $X$ 를 직접적인 변수로 제어할 수 있을까? $F(\theta)$ 대신 $G(X)$ 라는 함수를 르장드르 변환^{Legendre transformation}을 통해서 얻을 수 있다.

$\begin{equation} \tag{8} F(\theta) + G(X) = \theta \cdot X \end{equation}$
적률생성함수

$F(\theta)$ 의 르장드르 변환함수인

$G(X)$ 는 사실 조금 계산을 해보면 상대적 엔트로피인

$D_{KL}(P||P_0)$ 에 해당함을 확인할 수 있다.

$\begin{align} D_{KL}(P||P_0) &= \sum_x P(x) \log \frac{P(x)}{P_0(x)} \nonumber \\ &= \sum_x P(x) \log \frac{\exp(\theta \cdot x)}{Z} \nonumber \\ &= \sum_x \theta \cdot x P(x) – \log Z \nonumber \\ &= \theta \cdot X – F = G(X) \tag{9} \end{align}$
식 (8)에서

$\theta$ 와

$X$ 의 쌍대성에 의해 식 (7)의

$\partial F/\partial \theta = X$ 는 다음 식이 됨을 유추할 수 있다.

$\begin{equation} \tag{10} \frac{\partial G}{\partial X} = \theta \end{equation}$
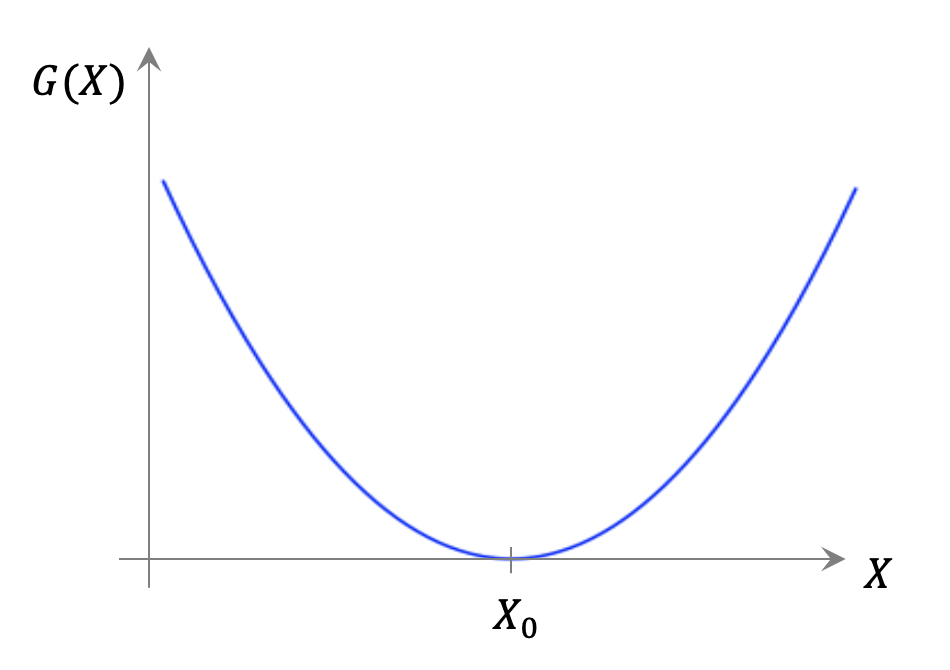
이렇게 얻은 엔트로피

$G(X)$ 는 데이터에 대한 많은 정보들을 함축하고 있다. 현재 우리의 관찰결과인

$P_0(x)$ 에서 얻은 평균이

$X_0$ 이다. 현재 데이터가 위치하는 곳은

$\theta=0$ 또는

$X=X_0$ 라고 간주할 수 있다. 그리고 이곳이 바로 오목함수

$G(X)$ 가 최소가 되는

$G(X_0)=D_{KL}(P_0||P_0)=0$ 인 지점에 해당한다.

우리는 전체 $X$ 공간에 대한 $G(X)$ 의 모습보다는 현재 관찰 데이터가 위치하는 $X=X_0$ 주변에 관심이 있기 때문에, 테일러 전개^{Taylor expansion}를 통해서 $G(X)$ 의 국지적 모습을 얻을 수 있다.

$\begin{align} G(X) &\approx G(X_0) + \frac{\partial G}{\partial X}(X-X_0) + \frac{1}{2} \frac{\partial^2 G}{\partial X^2}(X-X_0)^2 \nonumber \\ &\approx \frac{1}{2} C^{-1}(X-X_0)^2 \tag{11} \end{align}$
여기서 테일러 급수의 0차항은

$G(X_0)=0$ 으로 사라지고, 1차항 역시

$X=X_0$ 에서 기울기

$\partial G/\partial X=\theta$ 가

$0$ 으로 사라지게 된다. 이는

$X=X_0$ 에서

$G(X)$ 가 최소이므로 당연한 결과이다. 테일러 전개의 2차항의 계수는

$G(X)$ 의 곡률에 해당하는 것으로 사실 데이터

$\{x(t)\}$ 의 분산

$C$ 의 역수이다.

$\begin{equation} \tag{12} \frac{\partial^2 G}{\partial X^2}=\frac{\partial}{\partial X} \bigg( \frac{\partial G}{\partial X} \bigg) = \frac{\partial \theta}{\partial X} \end{equation}$
여기서

${\partial \theta}/{\partial X}$ 의 역수를 계산해 보자.

$\begin{equation} \tag{13} \frac{\partial X}{\partial \theta}=\frac{\partial}{\partial \theta} \bigg( \sum_x x P(x) \bigg)= \frac{\partial}{\partial \theta} \bigg( \sum_x \frac{x P_0(x) \exp(\theta \cdot x)}{Z(\theta)} \bigg) \end{equation}$
이 관계에서

$X=X_0$ 또는

$\theta=0$ 에서 아래 결과를 쉽게 확인할 수 있다.

$\begin{align} \bigg( \frac{\partial X}{\partial \theta} \bigg)_{\theta=0} &= \sum_x x^2 P_0(x) – \bigg( \sum_x x P_0(x) \bigg)^2 \nonumber \\ &= \mathbb{E}[x^2] – \mathbb{E}[x]^2 = C \tag{14} \end{align}$

$x$ 가 2차원 이상의 벡터인 경우

$C$ 는 공분산^covariance 행렬에 해당한다. 이로써 우리는 주어진 데이터에 해당하는 엔트로피 함수

$G(X)$ 를 식 (11)에서 완전히 정의할 수 있게 되었고, 이 함수의 기하학적 모양에서 데이터에 대한 정보를 마음껏 추출할 수 있게 된다.

예제

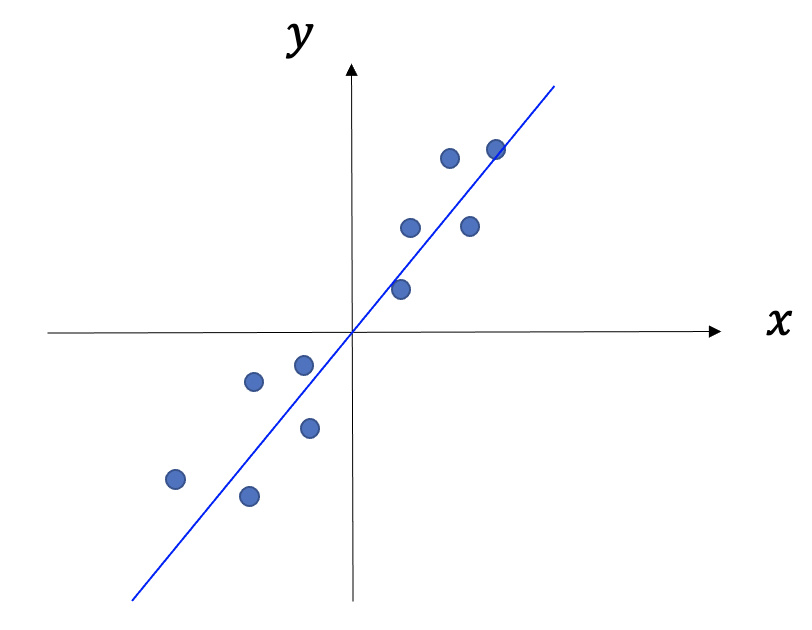
짝을 이루는 데이터 $\{ x(t), y(t)\}$ 의 선형모형 $y = Wx+b$ 을 생각해보자. 여기서 데이터를 가장 잘 맞추는 기울기 $W$ 는 아래와 같은 선형회귀 공식을 따른다. 각자 한번 유도해 보길 바란다.

$\begin{equation} \tag{15} W=\frac{\mathbb{E}[yx]-\mathbb{E}[y]\mathbb{E}[x]}{\mathbb{E}[x^2]-\mathbb{E}[x]^2} \end{equation}$

이제부터 우리는 통계학에서 가장 중요한 식 가운데 하나인 선형회귀 공식을 엔트로피 함수 $G(X)$ 로부터 얻어 보겠다. 먼저 주어진 데이터 $\{ x(t), y(t)\}$ 의 빈도수로부터 원시분포 $P_0(x,y)$ 를 얻을 수 있다. 그리고 데이터의 평균 $X= \sum_{x,y} x P(x,y)$ 와 $Y= \sum_{x,y} y P(x,y)$ 을 제한조건으로 가지면서 $P_0(x,y)$ 에 가장 가까운 시스템의 모분포를 얻는다.

$\begin{equation} \tag{16} P(x,y) = \frac{P_0(x,y) \exp(\theta \cdot x + \phi \cdot y)}{Z} \end{equation}$
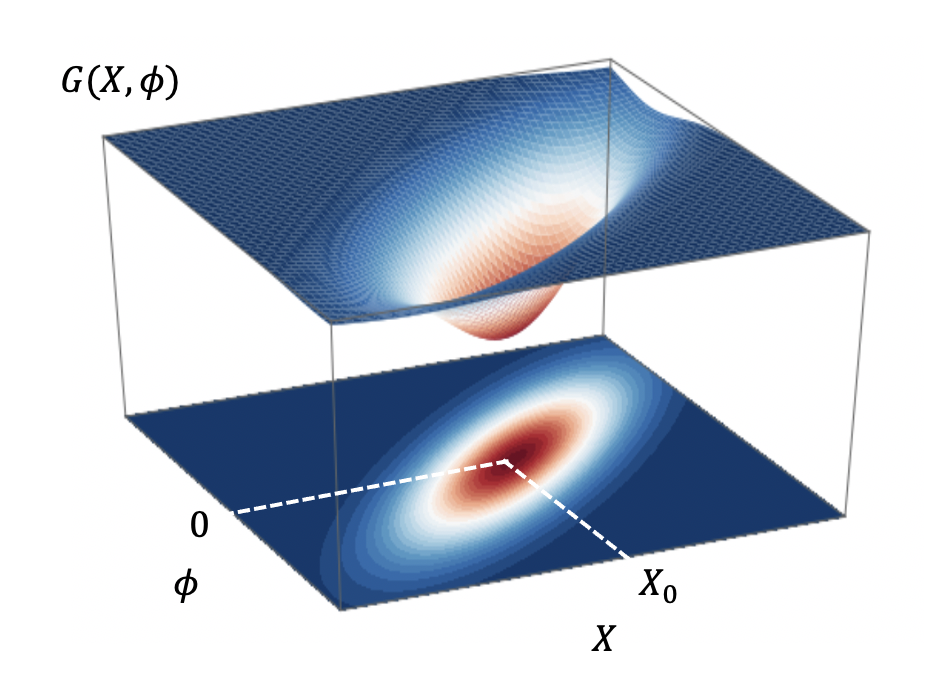
정규화 상수는

$Z=\sum_{x,y} P_0(x,y) \exp(\theta \cdot x + \phi \cdot y)$ 이다. 앞에서처럼 적률생성함수

$F(\theta, \phi) = \log Z(\theta, \phi)$ 에서 라그랑주 승수

$\theta$ 를 평균

$X$ 로 바꾸는 르장드르 변환을 통해서 엔트로피 함수

$G(X, \phi)$ 를 정의한다. 그리고 데이터가 위치하는

$X=X_0$ 근처에서 테일러 전개를 한다.

$\begin{equation} \tag{17} G(X,\phi) \approx G(X_0, \phi) + \frac{1}{2} C^{-1} (X-X_0)^2 \end{equation}$
위 식 (17)을

$\phi$ 에 대해서 미분을 해보자.

$\begin{align} \frac{\partial G(X, \phi)}{\partial \phi} &= \frac{\partial}{\partial \phi} \bigg( \theta \cdot X – F(\theta, \phi) \bigg) \nonumber \\ &= – \frac{\partial}{\partial \phi} \log Z = -\sum_{x,y} yP(x,y) = -Y \tag{18} \end{align}$
그리고 식 (17) 오른쪽 두 번째 항을 미분하면 다음과 같다.

$\begin{align} \frac{\partial}{\partial \phi} \bigg( \frac{1}{2} C^{-1} (X-X_0)^2 \bigg) = – C^{-1} \frac{\partial X_0}{\partial \phi} (X-X_0) \tag{19} \end{align}$
여기서

$\partial X_0/\partial \phi$ 를 더 계산해 보자.

$\begin{align} B \equiv \bigg( \frac{\partial X_0}{\partial \phi} \bigg)_{\phi=0} &=\frac{\partial}{\partial \phi} \bigg(\sum_{x,y} \frac{xP_0(x,y) \exp(\phi y)}{Z(\theta=0, \phi)} \bigg)_{\phi=0} \nonumber \\ &= \sum_{x,y} yx P_0(x,y) – \sum_{x,y} xP_0(x,y) \sum_{x,y} y P_0(x,y) \nonumber \\ &= \mathbb{E}[yx] – \mathbb{E}[y]\mathbb{E}[x] \tag{20} \end{align}$
이 결과들을 이용해서 식 (17)을 정리하면 다음 등식에 도착하다.

$\begin{equation} \tag{21} Y-Y_0 = C^{-1} B(X-X_0) \end{equation}$
여기서

$\delta X = X-X_0$ 변화에 대한 선형응답인

$\delta Y = Y – Y_0$ 를 결정하는

$W$ 는 다음과 같이 결정된다.

$\begin{equation} \tag{22} W=C^{-1}B =\frac{\mathbb{E}[yx]-\mathbb{E}[y]\mathbb{E}[x]}{\mathbb{E}[x^2]-\mathbb{E}[x]^2} \end{equation}$

놀랍게도 이는 위 선형회귀 공식 (15)와 정확하게 일치한다.[4] 각 샘플들의 선형관계 $y = Wx +b$ 를 데이터의 평균의 관계 $Y = WX +b$ 에서 구한 셈이다.이렇게 얻은 $W$ 는 엔트로피 함수 $G(X,\phi)$ 에서 변수 $X$ 와 $\phi$ 의 상호작용의 세기로 해석할 수 있다.

$\begin{equation} \tag{23} W = \frac{\partial Y}{\partial X} = -\frac{\partial}{\partial X}\bigg( \frac{\partial G}{\partial \phi} \bigg) = -\frac{\partial^2 G(X,\phi)}{\partial X \partial \phi} \end{equation}$

모시스템에서 임의의 유한한 데이터 $\{x(t)\}$ 가 주어졌을 때, 시스템을 이해한다는 것은 그런 데이터를 생성하는 모분포 $P(x)$ 를 찾는 것과 다르지 않다. 물론 신경망을 이용한 머신러닝이 이 작업을 훌륭하게 해내고 있다. 이번 글에서는 머신러닝 접근과 상호보완적인 접근이 될 수 있는 통계학적인 학습을 소개해 보았다. 모형과 데이터의 복잡도를 체계적으로 다루는 통계학적인 학습은 정보이론에 뿌리를 두고 있다. 특히 확률함수들 사이의 관계를 직접 다루는 정보기하학이 좋은 탐험 도구가 될 수 있음을 이번 글에서 살펴보았다.

물리학과 수학을 전공한 사람들이 머신러닝에 더 많이 기여하기를 기대하면서 네 번에 걸친 연재를 마친다. 그동안 관심을 가져주신 독자들에게 감사드린다.

참고문헌

Shun-ichi Amari, "Information geometry and its applications", Springer (2016).
https://franknielsen.github.io/FrankNielsen-distances-figs.pdf
Solomon Kullback, "Information theory and statistics", Dover (1997).
Danh-Tai Hoang, Juyong Song, Vipul Periwal, and Junghyo Jo, "Network inference in stochastic systems from neurons to currencies: Improved performance at small sample size", Physical Review E 99:023311 (2019).