[과학의 결정적 순간들] 1888년 9월, 맥스웰주의자들이 승리를 선언한 날

1888년 9월 6일, 영국 바쓰^Bath에서 열린 영국과학진흥협회 물리학회에서 영국 물리학자 피츠제랄드^{George Francis FitzGerald, 1851-1901}는 전자기파가 실험으로 입증되었음을 알렸다. 그는 맥스웰이 이론적으로 예측했던 전자기파의 검출 방법을 제안한 바 있었는데, 독일의 헤르츠^{Heinrich Hertz, 1857-1894}가 이 방법에 따라 전자기파의 공명에서 나타나는 강렬한 전기 스파크를 만들어냄으로써 전자기파의 존재를 확인시켜 주었던 것이다. 이로써 맥스웰의 전자기파 이론이 승리를 선언했다.

영광의 주인공은 영국 물리학자 제임스 클러크 맥스웰^{James Clerk Maxwell, 1831-1879}이었다. 고등학교 물리 시간에 처음 맥스웰의 이름을 들었을 때 당시 유명했던 커피 제품 이름이랑 같다는 것 외에 별 인상을 남기지 못했고, 실제로 수업 시간에도 잠깐 스치듯 지나가서 그가 얼마나 위대한 물리학자인지 알지 못했다. 대학 전자기 시간에 맥스웰 방정식을 배울 때도 이미 여러 학자들에 의해 발견된 법칙을 정리하고 거기에 숟가락 하나를 더 얹은 사람 정도라고 생각했다. 왜 이 법칙들에 맥스웰의 이름을 붙여야 하는지 이해가 되지 않았다. 왜 이런 생각을 하게 되었는지 잠깐 맥스웰 방정식([그림1])을 보자.

[그림1]에 나타난 전자기 현상에 대한 4개의 법칙을 맥스웰 방정식이라고 부른다. 첫 번째 가우스 법칙은 전하와 전기력선의 관계를 나타낸다. 첫 번째 가우스 법칙은 임의의 공간에 들어가는 전기력선의 양과 그 공간에서 나오는 전기력선의 양에 차이가 있을 때 공간 안의 전하의 총합이 0이 아님을 의미하며, 이때 공식 (1)에서 D는 전기력선의 밀도를 의미한다. 두 번째 가우스의 자기법칙은 일정한 공간에 들어오는 자기력선의 양과 전기력선의 양이 항상 같다는 것을 의미한다. 이는 자기력선이 언제나 폐곡선을 그린다는 것을 의미하며, 또한 자기력선에는 전기의 (+) 또는 (-) 전하처럼 단독으로 존재하면서 열린 전기력선을 만드는 물리적 존재, 즉 홀극^monopole이 존재하지 않는다는 것을 의미한다.

세 번째 법칙은 자기장의 시간적 변화가 전기장을 유발한다는 것을 의미하는데, 코일에 자석을 넣었다 뺐다 했을 때(즉, 자기장의 시간적 변화) 코일에 전기장이 형성되어 전류가 흐른다는 것을 의미한다. 네 번째 앙페르의 법칙은 전류가 흐르는 도선 주변에 자기장이 형성되는 것을 표현한 것인데, 자기장의 강도(H)가 변위 전류와 일반 전류의 합으로 나타난다는 것을 의미한다. 이때 D는 전기력선의 밀도, J는 일반전류밀도를 나타내는 물리량인데, 이중 \(\frac { \partial D }{ \partial t } \)는 전기력선의 시간적 변화로 인한 전류를 의미하고, J는 회로에 흐르는 전류를 의미한다.

그저 방정식 각각의 이름만 보면, 맥스웰은 쿨롱이나 가우스, 패러데이, 앙페르가 발견한 법칙을 한자리에 모으고 거기에 전기변위(\(\frac { \partial D }{ \partial t } \))의 개념을 더했을 뿐인데, 왜 맥스웰에게 법칙을 발견한 영예를 부여했던 것일까? 기존에 난립해 있던 전자기 관련 법칙을 수학화하면서 수학적 일관성을 이끌어 냈다는 점, 즉 “수학적 종합”이라는 말로 그의 기여를 평가하기도 하지만, 맥스웰의 공헌은 “수학화”라는 말로는 부족하다. 이제 그 이야기로 들어가 보자.

맥스웰이 전자기 연구에 본격적으로 뛰어든 것은 1854년 케임브지리 대학의 악명 높은 졸업 시험 수학 트라이포스^{mathematical tripos}를 마친 직후였다.¹ 졸업 시험을 2등으로 마친 맥스웰은 패러데이의 <전기에 관한 실험 연구^{Experimental Researches in Electricity}>를 읽으면서 전자기학 연구를 시작한다.

패러데이는 전기와 자기 간의 상호작용, 그리고 전자기와 광학 간의 상호작용을 물리적인 현상으로 구현하는 데 압도적인 능력을 지닌 사람이었다. 코일 안팎의 자석의 운동으로 전류를 유도하는 실험, 전기와 자기의 상호작용의 본질이 회전 운동이라는 것을 보인 실험 등 사람들의 눈앞에 특정 현상을 펼쳐내는 데 타의 추종을 불허했다. 하지만 조판공 도제 출신으로 독학하며 과학을 공부한 패러데이에게 수학은 언제나 높은 장벽이었다. 특히 19세기 중반 영국에서는 프랑스의 미적분학을 받아들여, 열, 빛, 전기, 자기 현상을 미적분학으로 분석하는 것이 과학계의 주된 흐름이었는데, 패러데이는 이 흐름의 바깥에 외로이 서 있었다.

여기에 뉴턴으로부터 이어지는 원거리력^{action at a distance} 대신 힘의 선과 장^field이라는 개념으로 전자기 현상을 설명했던 패러데이의 시도를 당대의 주류 학자들은 이해하기 힘들었다. 당시 독일에서는 빌헬름 베버^{Wilhelm Weber, 1804-1891}가 쿨롱 법칙과 앙페르 법칙을 결합하여 원거리력으로 설명하려는 시도가 있었는데, 영국에서조차도 베버식의 접근을 더욱 편안하게 여겼다. 가우스의 법칙과 앙페르의 법칙, 쿨롱의 법칙 모두 원거리력 개념을 바탕으로 만들어진 것이었기 때문에, 원거리력 이론은 위 법칙들로 증명된 것처럼 보이기도 했다. ([그림1]에서 보인 각각의 법칙은 맥스웰 방정식에 편입된 후 약간의 변형을 거친 것이다. 원래의 가우스 법칙이나 쿨롱 법칙, 앙페르의 법칙은 [그림1]과는 수학적 형태가 달랐다.)

맥스웰이 시작한 것은 바로 패러데이의 힘의 선과 장 개념의 수학화였다. 그 힌트는 같은 스코틀랜드 출신 선배인 윌리엄 톰슨^{William Thomson, 1824-1907 2}으로부터 얻을 수 있었다. 톰슨은 푸리에^{Jean-Baptiste Joseph Fourier, 1768-1830}의 열전도 이론과 쿨롱^{Charles-Augustin de Coulomb, 1736-1806}의 정전기 원거리력 이론의 수학적 형태가 동일하다는 점에 주목했다. 수학적으로 두 이론이 같다면, 물리적 현상도 같지 않겠는가. 톰슨은 수학적 공식의 동일성으로부터 물리적 현상의 유사성을 끌어내는 수학적 유비의 방법을 발전시켰다.

맥스웰은 반대의 방법을 사용했다. 푸리에가 열전도 이론에서 열을 유체의 흐름으로 이해했던 것처럼 패러데이의 전자기 힘의 선과 전자기장도 유체의 흐름으로 가정하면, 물리적 현상의 유사성에 기반해서, 푸리에가 열전도에서 사용한 수학적 기법을 패러데이 힘의 선과 장 개념에 적용할 수 있지 않을까. 맥스웰은 작업에 착수했다.

맥스웰은 전자기의 힘의 선을 압축이 불가능한 유체의 흐름으로 가정하고, 유체가 시작되는 공급원^source과 유체가 나가는 배수구^sink가 있는 유체 유동 모형을 만들었다. 그 사이를 흐르는 유체는 공급원에서 배수구까지 이어지는 막대 모양의 긴 튜브가 여러 개 모여 있는 튜브 다발로 상정했다. 튜브의 단면적은 제각각일 수 있는데, 단위 시간당 하나의 튜브에 흐르는 유체의 양은 일정하다. 따라서 단면적이 넓은 튜브보다는 좁은 튜브에서 유체의 속도가 빨라진다. 이제 전자기 현상과 비교하면, 공급원은 (+) 전하, 배수구는 (-) 전하가 되고 그사이에 형성된 힘의 선 하나하나는 유체 튜브 하나하나에 대응된다.

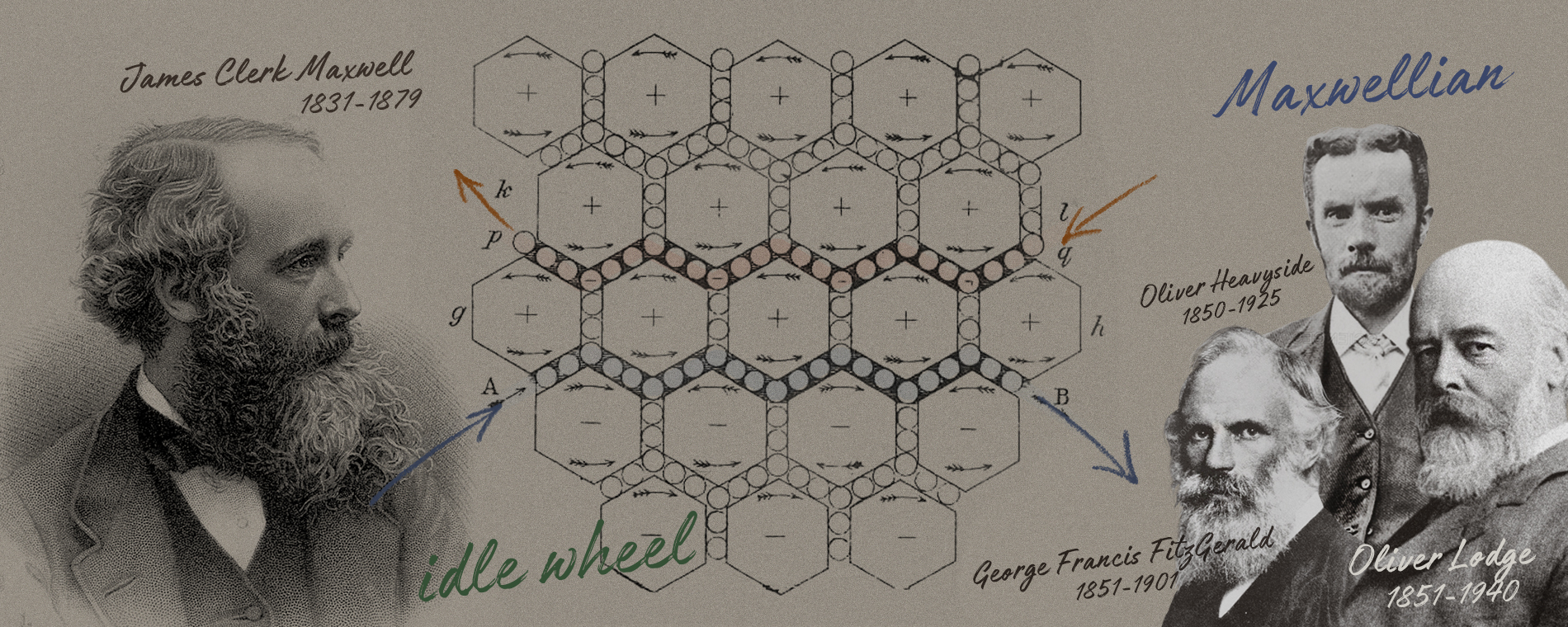
맥스웰은 푸리에의 열전도 이론에 관한 수학 공식을 적용하여 전자기 힘의 선과 장의 수학적 표현을 끌어냈다. 이를 통해 그는 쿨롱의 법칙을 전기력선과 장으로 설명할 수 있다는 것을 보였다. 그동안 전하 사이의 원거리 작용으로만 이해해왔던 정전기력을 패러데이의 힘의 선과 장으로도 유도할 수 있다는 것을 보여준 것이다. 맥스웰은 이에 관해 <패러데이의 힘의 선에 관하여>(1855-1856)라는 논문을 출판했다.1861년 출판된 <물리적 힘의 선에 관하여>에서 맥스웰은 유명한 “유동바퀴^{idle wheel}”모형을 도입했다. 기존의 유체 시스템이 전기나 자기 현상 각각을 설명할 수는 있었지만, 패러데이의 발견에서 가장 중요한 전기와 자기의 상호작용을 설명할 수 없었던 점을 보완하기 위해 맥스웰은 완전히 새로운 모형을 제시했다.([그림2])

유동바퀴 모형은 육각형 모양의 소용돌이 분자와 그 사이를 흐르는 작은 구형의 입자들(유동바퀴), 그리고 두 개의 도체 AB와 pq로 구성된다. 도체 A에서 B로 흐르는 전류는 A와 B 사이에 존재하는 작은 유동바퀴의 운동으로 표현된다. 유동바퀴가 움직임에 따라 그 주위의 육각형 소용돌이 분자들은 바퀴의 흐름에 따라 회전하여 AB의 위쪽에 접한 소용돌이 분자들(gh)은 반시계 방향으로, 아래 접한 소용돌이 분자들은 시계방향으로 회전한다. gh의 회전은 도체 pq에 있는 유동바퀴의 흐름을 만들어내는데, 이때 유동바퀴는 q에서 p로 흐르면서 소용돌이 분자 kl의 회전을 유발한다.

모형에서 작은 유동바퀴의 운동은 전류의 흐름, 소용돌이 분자의 회전은 자기력선을 의미한다. 맥스웰은 유동바퀴 모형으로 전류의 흐름이 주위에 자기장을 발생시킨다는 것을 표현했다(유동바퀴가 소용돌이 분자를 회전시켜 자기장 발생). 또 AB에 흐르는 전류로 인해 도체 pq에 유도전류가 발생하는 것을 보였고, 유도전류의 흐름이 원래 전류의 흐름과는 반대가 된다는 것도 보였으며, 소용돌이 분자와의 마찰로 인해 유도전류의 흐름이 곧 사라지는 것까지 표현했다.

이후 맥스웰은 소용돌이 분자가 탄성을 지니고 이로 인해 소용돌이 분자에 탄성 변형이 일어난다는 가정을 추가로 도입했다. 탄성 변형의 효과로 인해 소용돌이 분자가 힘을 받으면 변형되었다가 다시 원상태로 복귀해서 작용을 전달하기까지는 얼마간 시간이 걸렸다. 맥스웰은 탄성 변형을 도입하여, 전기와 자기의 효과가 공간적으로 전달될 때는 항상 시간이 걸린다는 것을 모델로 구현해냈다. 힘 전달에 시간이 걸리는 것은 힘의 선 이론과 원거리 작용과의 좁힐 수 없는 차이에 해당했는데, 이 모델로부터 맥스웰은 힘이 전달되는 데 걸리는 시간, 즉 전자기파가 전달되는 속도가 빛의 속도와 동일하다는 것까지 유도해낼 수 있었다. 그리고 이 모형으로부터 앙페르의 법칙과 쿨롱의 법칙을 포함한 맥스웰 법칙을 모두 유도해내는 데 성공했다.

1861년 유동바퀴 모델의 성과를 정리하면 다음과 같다. 첫째, 그는 힘의 선과 장 개념을 구현할 수 있는 기계적 모형을 만들고, 그로부터 원거리 작용으로 찾아냈던 앙페르 법칙과 쿨롱 법칙을 유도하는 데 성공했다. 이로써 힘의 선 개념에 대한 원거리 작용 이론의 우위가 사라졌다. 둘째, 맥스웰은 유동바퀴 모델을 이용해 원거리 작용에서는 하지 못했던 새로운 예측, 즉 전자기파의 전파 속도가 광속에 해당할 것이라는 예측을 이끌어냈다. 이제 전자기파 속도 측정 실험은 두 이론 중 누가 옳은지 판가름하는 결정적인 역할을 수행하게 될 터였다.

1864년에 발표한 <전자기장에 대한 동역학적 이론>부터 1873년에 출판한 <전기와 자기에 관한 논고>에 이르기까지 맥스웰은 유동모형 같은 기계적 모델을 최대한 자제하면서 전자기장 이론을 발전시켜 나갔다. 탄성 매질에 대한 최소한의 가정만을 가지고 탄성 매질의 구체적인 작동 메커니즘에 대한 언급은 최대한 피하면서, 일반화된 이론으로 나아가려 했다. 19세기 과학계, 그중에서도 영국 과학계에서 자연의 물리적 작동방식을 기계적 모형의 구체적 운동으로 구현하는 것은 낯선 일이 아니었다. 윌리엄 톰슨은 특정 물리 현상에 대해 기계적 모형을 생각해 내지 못한다면 그것은 현상을 제대로 이해하지 못한 것이라고 말하기까지 했다. 하지만 기계적 모형을 통한 유비^{mechanical analogy}는 그저 유비일 뿐이지 자연의 실제 작동 방식을 의미하지 않는다는 것은 당시의 과학자들도 동의하는 바였다. 따라서 맥스웰은 발견의 도구로서 기계적 유비를 활용하는 것은 1861년 논문까지로 한정하고, 1864년 논문부터는 그 유비를 벗어나 일반화를 추구했던 것이다.

하지만 맥스웰의 이론은 쉽게 받아들여지지 않았다. 오늘날 맥스웰 방정식이 4개의 방정식으로 이루어진 것과 달리, 당시 맥스웰 방정식은 20개의 변수로 쓰인 20개의 방정식으로 구성되었다. 전자기파의 속도는커녕, 전자기파를 만들어내는 것조차 아직 실험적으로 구현된 적이 없었다. 전자기파는 그저 논문 속에서, 수학적으로만 존재했던 것이다. 1879년 11월 5일, 맥스웰은 위암으로 세상을 떴다. 비록 20년 가까이 해온 전자기론 연구가 학계에 수용되는 것을 보지는 못했지만, 열역학의 분자 운동론, 맥스웰 분포 곡선과 통계역학, 시각에 대한 연구, 토성의 고리 안정성에 대한 연구, 케임브리지 대학 캐번디쉬 연구소의 초대 소장, 영국 과학진흥협회에서 저항 표준의 절대 측정을 주도하여 영국의 저항 단위를 국제 단위로 정립시키는 등 위대한 과학자로 기억되기에 맥스웰의 업적은 차고 넘쳤다.

세상을 뜨기 직전까지 맥스웰은 <전기와 자기에 관한 논고> 2판을 준비 중이었다. 하지만 2판이 나왔다고 할지라도 그의 책이 물리학계를 설득할 가능성은 크지 않았을 것 같다. 패러데이의 이론이 이상해 보였던 것만큼이나 맥스웰의 책도 수학적으로 어려우면서 투박했고, 대학 때부터 그래왔듯이 계산 실수도 많아서 신뢰성을 깎아 버리는 일도 잦았다. 어쩌면 맥스웰의 책은 위대한 과학자가 남긴 이해하기 힘든 이론으로 끝나버렸을지도 모른다. 하지만 다행스럽게도 맥스웰의 이론에 열광한 젊은 학자들이 그의 이론을 수학적으로 세련되고 물리적으로 수용 가능한 형태로 바꾸는 일에 뛰어들었다. “맥스웰주의자^Maxwellian”로 알려진 이들은 1888년 배쓰의 승리 선언을 이끌어 낸 사람들이었다.

맥스웰주의자 중 가장 독특한 인물인 헤비사이드^{Oliver Heaviside, 1850-1925}의 이야기부터 시작해보자. 헤비사이드도 패러데이처럼 독학으로 공부한 과학자이지만, 독학이라는 점 때문에 수학에 발목을 잡혔던 패러데이와 달리 헤비사이드는 수학으로 날개를 달았던 사람이다. 넉넉하지 못한 집안에서 태어난 헤비사이드는 초등학교 수준의 정규 교육만 받았다. 다행이었던 것은 휘트스톤 브리지를 만든 찰스 휘트스톤이 삼촌뻘이었던 덕에 어려서부터 전기에 관심을 가지게 되었다는 점이다. 삼촌의 도움을 받아 전신 기사^{telegraph engineer}가 되었고, 전신에 관한 논문도 출판하여 윌리엄 톰슨이나 맥스웰의 눈에 띄기도 했다.

1873년 헤비사이드는 맥스웰의 <전기와 자기에 관한 논고>를 처음 접했다. 너무나 멋진 책이었지만 산수와 삼각함수 정도밖에 알지 못했던 그가 읽기에는 너무 어려웠다. 이후 수년간 헤비사이드는 맥스웰의 책을 이해하기 위해 수학을 공부했고, 그 과정에서 맥스웰의 수학 공식을 더욱 간단하고 세련되게 표현하는 방법을 개발했는데, 그것이 바로 벡터였다. 그는 벡터의 “회전^curl”과 “발산^divergence” 연산자를 이용하여 맥스웰의 공식을 현재 우리가 쓰는 것과 같은 4개의 공식으로 정리했다. 헤비사이드를 통해 맥스웰의 방정식은 간단하면서 명쾌한 형태로 자리 잡게 되었다.

바쓰에서 헤르츠의 실험을 소개한 피츠제랄드도 대표적인 맥스웰주의자였다. 아인슈타인 특수상대성 이론에 나오는 로렌츠-피츠제랄드 수축의 바로 그 피츠제랄드이다. 1879년 2월 맥스웰은 건강이 악화되어가는 중에도 논문 심사를 맡았는데, 논문의 저자가 바로 아일랜드 트리니티 칼리지의 펠로우였던 피츠제랄드였다. 피츠제랄드는 논문에서 전자기 빛의 이론을 반사, 굴절, 광자기 현상에까지 적용함으로써 맥스웰 전자기 이론의 확장을 꾀했다. 후에 피츠제랄드는 빠르게 진동하는 전류로 전자기파를 만들어낼 수 있을 것이라고 예측했는데, 헤르츠의 실험 덕에 자신의 예측이 맞았음을 바쓰에서 선언할 수 있었다.

피츠제랄드의 동년배 친구였던 올리버 로지^{Oliver Joseph Lodge, 1851-1940}도 빼놓을 수 없는 맥스웰주의자였다. 로지는 맥스웰 이론을 쉽게 전달하는 해설자 역할에 탁월한 재능을 보였다. 그는 구슬이 달린 줄과 도르래를 이용해 맥스웰의 전자기파가 에테르를 통해 전달되는 기계적 모형을 고안했으며, 해당 모형과의 유비를 통해 전기 전도와 유전 분극들을 이해하기 쉬운 방식으로 설명했다. 또한 로지는 피츠제랄드와 함께 전자기파를 발생, 검출하는 방법을 처음으로 고안했으며, 라디오와 같은 활용 영역으로 맥스웰의 전자기파가 확장하는 데 기여했다.

영국 맥스웰주의자들의 수많은 노력 덕에 난해했던 맥스웰의 전자기파 이론은 좀 더 이해 가능한 형태로, 좀 더 수학적으로 세련된 형태로 바뀌었으며, 더 많은 전자기 현상과 광학 현상으로까지 확대 적용되었다. 또한 이들의 제안으로 전자기파는 실험적으로 검출 가능한 존재가 되었다. 그 검증은 영국 맥스웰주의자들이 아닌, 독일의 헤르츠에 의해서 이루어지기는 했지만 말이다.

맥스웰과 맥스웰주의자들의 관계는 하나의 과학 이론이 매우 집단적인 협력의 성과물임을 보여준다. 우리는 보통 뉴턴의 고전역학, 아인슈타인의 상대성 이론 등 하나의 이론에 한 명의 연구자 이름을 붙이는 데 익숙하지만, 뉴턴이나 아인슈타인 단독으로는 오늘날과 같은 완성도를 갖춘 이론이 등장하지 못했을 것이다. 1687년 <프린키피아>에서 시작한 뉴턴의 고전역학은 라플라스의 <천체역학>(1799-1825)에 이르기까지 100년이 넘는 기간 동안 수많은 학자의 손을 거쳐 수정과 보완을 거듭해 오늘날의 형태를 갖추었다. 아인슈타인의 상대성 이론 역시 100년이 넘은 지금까지도 계속해서 발전하고 있는 중임을 21세기 노벨 물리학상을 통해 확인할 수 있다.

마찬가지로 맥스웰주의자들의 공헌을 뺀다면, 맥스웰 전자기 이론이 이후에 이룬 엄청난 성공과 기술적 성과를 설명할 수 없을 것이다. 오늘날 헤비사이드, 피츠제랄드, 로지는 과학사학자들만 기억하는 이름이 되었지만, 이들은 맥스웰만큼이나 당대 과학의 발전에 기여했던 사람들이다. 우리가 그들의 이름을 기억해야 하는 이유는, 지금도 연구 현장에서 일하는 수많은 과학자들 역시 그들처럼 훗날 역사에 이름을 각인시키지는 못 할지라도, 과학이라는 거대한 퍼즐의 아주 작은 조각들을 맞춰나가는 데 일조하고 있기 때문일 것이다.