부도체의 재발견: 부도체의 완벽한 분류

물질은 전극을 연결하였을 때 전류가 흐르는지 흐르지 않는지를 기준으로 도체와 부도체로 나뉜다. 전류가 흐르면 도체이고, 전류가 흐르지 않으면 부도체이다. 수많은 고체 물질을 전도특성을 기준으로 두 가지로 간단명료하게 분류할 수 있다는 건 정말 멋진 일이 아닐 수 없다. 그런데 15년 전 즈음에 이런 이분법으로 분류할 수 없는 이상한 물질 상태가 있다는 사실이 알려졌다. 새로운 고체 물질은 물질 내부로는 전류가 흐르지 않지만, 물질 표면으로는 전류가 흐른다. 도체도 아니고 부도체도 아닌 어정쩡한 상태가 존재하는 것이다.

얼핏 생각에 표면에 존재하는 도체부분만 잘 떼어내면 결국 부도체로 만들 수 있을 것 같지만, 안타깝게도 도체 껍질을 한 꺼풀 벗겨내면, 새로운 표면이 다시 도체가 된다. 표면의 전도 특성이 그냥 표면만의 문제가 아닌 것이다. 물질 자체가 단순 부도체로의 변화에 저항성이 있는 것이다. 오늘날 이런 이상한 물질을 위상 부도체^{topological insulator}라고 부른다. 고체의 분류에 뜬금없이 어려운 수학적 개념인 위상^topology이라는 말이 붙는 이상한 일이 벌어진 것이다.

부도체는 사실 가장 단순하고 기본적인 물질의 상태이다. 예를 들어 간단한 형태의 부도체로 닫힌 에너지 껍질^{closed energy shell}을 가진 원자들의 주기적인 집합을 들 수 있다. 여기서 에너지 껍질^{energy shell}은 한 원자에 속박된 전자가 가질 수 있는 에너지 준위를 의미한다. 양자역학에 따르면 원자핵에 속박된 전자의 에너지는 연속적으로 변할 수 없고 불연속적이고 양자화된^quantized 값을 가지는데, 각 양자화된 에너지 준위를 에너지 껍질이라고 부른다.

하나의 에너지 껍질이 전자로 꽉 차서 닫히게 되면, 그다음 전자는 에너지 갭^{energy gap}만큼 에너지가 더 높은 그다음 에너지 껍질을 채우게 된다. 결국 닫힌 에너지 껍질을 가진 원자는 외부에서 자극을 받더라도, 자극에 의한 에너지 변화가 에너지 갭보다 작은 경우 아무런 반응을 하지 않는다. 이런 원자들의 집합으로 만들어진 결정은 외부의 약한 전기장에 대해서 반응하지 않는데 이는 전자를 들뜨게 하려면 일정한 정도 이상의 에너지가 전자에 가해져야 하기 때문이다. 이는 곧 전류가 흐르지 않는 부도체 상태가 됨을 의미한다. 이런 형태의 간단한 부도체를 원자 부도체^{atomic insulator}라고 부른다.

위의 설명을 들으면, 부도체는 외부 자극에 아무 반응을 보이지 않는 재미없는 물질상태라는 생각이 들 법도 하다. 하지만 최근에 발견된 위상 부도체^{topological insulator}의 존재는 위에서 언급한 원자 부도체와는 구별되는, 흥미로운 성질을 가진 새로운 부도체 상태가 존재함을 의미한다.[1] 간단히 이야기해서, 위상부도체는 고체 내부로는 전류가 흐르지 않고 표면으로만 전류가 흐르는 독특한 성질을 가지는 부도체를 말한다. 표면에 존재하는 도체상태는 고체 속 전자 파동함수가 가지는 독특한 위상학적 성질 때문에 나타나는데, 이로 인해 위상^topology라는 말이 부도체 앞에 붙는다. 위상 부도체 표면의 금속 상태는 불순물에 의한 산란에 큰 영향을 받지 않고, 고체 내부의 부도체 상태가 유지되는 한 전도 특성이 보존된다.

이런 형태의 전형적인 위상 부도체의 존재는 2005년에 처음 이론적으로 예측이 되었고, 2007년, 2008년에 2차원 그리고 3차원 위상 부도체의 존재가 실험적으로 규명되었다.[1] 위상 부도체의 이론적, 실험적 발견은 기존 고체의 물성을 이해하는 방식의 근본적인 변화를 가져왔고, 그 후 고체 속 파동함수의 위상 성질이 고체의 물성을 이해하는 가장 기본 개념으로 자리잡게 되었다. 또한 초기 위상 부도체의 발견 이후, 위상 준금속^{topological semimetals}, 위상학적 결정 부도체^{topological crystalline insulators}, 위상 초전도체^{topological superconductors} 등 새로운 형태의 위상학적 고체상태가 발견되었다. 이번 글에서는 불과 15년 정도의 짧은 기간 동안 일어난 고체 물성을 기술하는 근본적인 패러다임의 변화, 그중에서도 부도체를 이해하는 방식의 변화를 간단히 정리해보고자 한다.

부도체의 양자역학: 에너지 띠 구조

위에서 가장 간단한 형태의 부도체로, 닫힌 에너지 껍질을 가진 원자들의 집합인 원자 부도체를 이야기했다. 닫힌 에너지 껍질의 의미를 이해하기 위해서는 원자에 속박된 전자의 에너지가 불연속적으로 양자화된다는 양자역학적 개념이 필요한데, 이는 곧 원자 부도체를 정의하려면 양자역학적 개념이 필수적으로 요구된다는 것을 의미한다.

원자 하나에 속박된 전자의 에너지는 연속적으로 변할 수 없고, 양자화된 불연속적인 값을 가지게 된다. 이런 전자의 파동함수는 원자핵을 둘러싸는 여러 개의 불연속적 에너지 껍질로 나타난다. 이런 원자를 공간에 규칙적으로 배열하여 결정상태를 만들면, 이웃한 원자에 속박된 전자 파동 사이에 중첩이 생기고, 이로 인해 결정 속 에너지 껍질의 집합은 에너지 띠^{energy band}를 형성하게 된다.

에너지 띠의 의미를 좀 더 명확히 이해하려면, 고체 결정이 병진 대칭성^{translational symmetry}이 있는 주기적인 구조^{periodic structure}라는 점에 주목해야 한다. 전자가 주기적인 포텐셜 하에서 움직일 경우 전자의 양자역학적 상태를 기술하는 파동함수는 결정 운동량^{crystal momentum} 공간의 블로흐 상태^{Bloch state} \(u_{n}(k)\)로 기술이 되고, 해당 에너지 고유값 \(E_{n}(k)\) 역시 운동량 \(k\)의 함수로 주어진다. 여기서 정수 \(n\)은 에너지 띠를 구분하는 숫자다. 실공간에서의 주기성은 운동량 공간에서의 주기성으로 나타나고, 이는 곧 전자의 에너지 고유값 \(E_{n}(k)\) 역시 운동량 공간에서 주기성을 가지게 됨을 의미한다. 이렇듯 운동량 공간에서 주기성을 가지고 존재하는 전자 에너지 고유값의 집합을 격자의 에너지 띠 구조^{energy band structure}라고 부르는데, 고체 안에는 일반적으로 무수히 많은 에너지 띠가 복잡하게 얽혀 있다.

전자는 페르미온이기 때문에 고체 속 전자들은 파울리 배타원리^{Pauli exclusion principle}를 만족하며 에너지가 낮은 띠부터 순차적으로 차곡차곡 채운다. 극저온의 부도체에서 낮은 에너지 띠부터 전자를 순차적으로 채웠을 때 전자가 꽉 찬 가장 높은 에너지 띠를 원자가띠^{valence band}라고 하고, 전자가 차지 않은 에너지 띠 중 가장 낮은 에너지 띠를 전도띠^{conduction band}라고 한다. 위에서 정의한 원자 부도체의 경우 꽉 찬 원자가띠와 텅 빈 전도띠 사이에 에너지 갭이 존재하고 이로 인해 전기장에 의한 에너지 변화가 에너지 갭보다 작게 되면 전류가 흐르지 않는다.

사실 원자가띠와 전도띠는 부도체보다는 반도체의 에너지 띠 구조 설명에 등장하는 개념이다. 하지만 에너지 띠 구조상 부도체와 반도체는 사실 굉장히 비슷하다. 에너지 갭의 크기만 다를 뿐이다. 이는 곧 에너지 갭의 크기를 연속적으로 줄일 수 있으면 부도체를 연속적으로 반도체로 변형시킬 수 있다는 뜻이 되는데, 이렇게 에너지 갭을 유한한 크기로 유지하면서 연속적인 변형을 통해 연결될 수 있는 상태들을 위상학적으로 동등한^{topologically equivalent} 상태라고 부른다. 위상학적 동등성의 개념을 조금 더 확장하면 안정된 위상학적 동등성^{stable topological equivalence}이라는 개념을 도입할 수 있다.

안정된 위상학적 동등성은 원자가띠와 전도띠 사이의 에너지 갭을 유한하게 유지하지만 위상 성질이 없는 전자가 찬 에너지띠 개수의 변화는 허용하는 연속적인 변형을 생각하고, 이런 변형에 대해 두 물질의 에너지 띠구조가 연속적으로 연결될 수 있는지를 묻을 수 있다. 조금 복잡한 개념이지만, 이렇게 위상학적 동등성의 개념을 확장하면 부도체를 위상 숫자를 기반으로 체계적으로 분류하는 것이 가능해진다. 또한 이 기념을 이용하면 모든 원자 부도체는 위상학적으로 동등하다는 결론도 얻게 된다. (물론 결정 대칭성을 더 조심스럽게 고려하면, 원자 부도체들도 위상학적으로 구분이 가능한데, 이에 대해서는 후반부에 논의하겠다.) 그렇다면 모든 부도체가 원자 부도체와 위상학적으로 동등한가 하는 질문을 해볼 수 있다. 물론 정답은 “아니오”가 된다. 왜냐하면 앞에서 언급한 위상 부도체는 어떤 형태의 원자 부도체와도 연속적인 변형을 통해 연결될 수 없기 때문이다.

양자 홀 상태^{Quantum Hall state}

원자 부도체와 위상학적으로 동등하지 않은 부도체 상태의 대표적인 예가 바로 양자 홀 상태^{quantum Hall state}이다.[2] 양자 홀 상태는 2차원 금속에 수직방향으로 자기장을 걸면 나타난다. 수직방향 자기장 하에서 전자는 \(\omega_c\)의 진동수를 가지고 원운동을 하는데, 원운동의 궤적은 양자화되고 해당 전자의 에너지 역시 다음과 같이 양자화된 값을 가진다.

$$E_m=\hbar\omega_c\left(m+\frac{1}{2}\right),~~(m=0,1,2,3,\cdots)$$

이렇게 양자화된 전자의 에너지 준위들을 란다우 준위^{Landau level}라고 부른다. 밑에서부터 \(N\)개의 란다우 준위 \((m=0,1,…,N-1)\)가 전자로 꽉 채워지고, 그 뒤에 있는 란다우 준위 \((m=N,N+1,…)\)가 텅 빈 경우, 전자가 가득 찬 \(N\)번째 란다우 준위와 텅 빈 \(N+1\)번째 란다우 준위 사이에는 \(\hbar\omega_c\)만큼의 에너지 갭이 존재한다. 이런 상황은 마치 원자 부도체의 전자 구조와 비슷하다. 하지만 원자 부도체와 양자 홀 상태 사이에는 큰 차이가 있다. 약한 전기장을 걸어도 전류가 흐르지 않는 원자 부도체와 달리, 양자 홀 상태에서는 2차원 물질 가장자리를 따라 시계 방향 혹은 반시계 방향으로 홀 전류^{Hall current}가 흐른다.

뿐만 아니라 홀 전도도는 \(\sigma_{xy}=\pm N\frac{e^2}{h}\)로 주어지는 양자화된 값을 가진다. 여기서 \(e\)는 전자의 전하, \(h\)는 플랑크 상수, \(N\)은 전자가 꽉 찬 란다우 준위의 개수이다. +, – 부호는 홀 전류가 흐르는 방향이 시계 방향인지 반시계 방향인지를 나타내고, 이는 자기장이 위쪽으로 걸렸는데 아래쪽으로 걸렸는지를 나타낸다. 양자 홀 상태의 가장 중요한 성질인 양자화된 홀 전도도는 \(\frac{1}{10^9}\)의 정확도로 측정이 되었으며 이런 정확한 측정은 홀 전도도가 위상 불변량^{topological invariant}이라는 사실에 덕분에 가능했다.

양자 홀 상태의 양자화된 홀 전도도가 위상 불변량이라는 말의 의미를 좀 더 생각해보자. 위상학적 불변성은 연속적인 변화에 대해 불변인 성질을 의미한다. 양자 홀 상태의 경우는 2차원 물질에 연속적인 변형을 가해주어도 \(N\)번째 란다우 준위와 \(N+1\)번째 란다우 준위 사이의 에너지 갭이 유한하게 유지되는 한 홀전도도는 같은 값 \(\sigma_{xy}=N\frac{e^2}{h}\)을 유지한다. 이는 홀 전도도가 위상 불변량이라는 의미이다. 원자 부도체의 경우는 일반적으로 홀 전류가 흐르지 않기 때문에 양자 홀 상태와 구분이 가능하고 두 물질 상태는 위상학적으로 구분이 된다. 즉 원자 부도체는 연속적인 변형을 통해 양자 홀 상태로 전이가 불가능하다. 원자 부도체를 양자 홀 부도체로 전이시키려면, 원자가띠와 전도띠 사이의 에너지 갭이 영이 되는 불연속적 과정을 거쳐야 하는데, 해당 상전이 현상을 위상 상전이^{topological phase transition}라고 부른다.

양자 홀 상태의 양자화된 홀 전도도는 해당 전자 파동함수의 고유한 성질이다. 양자화된 홀 전도도와 전자 파동함수의 관계에 대해서 좀 더 자세히 알아보자. 란다우 준위는 전자의 에너지띠에 해당한다. 원자 부도체의 경우와 달리 양자 홀 상태에서는 결정 운동량 k를 정의할 때 약간 주의가 필요하다. 자속 양자^{magnetic flux quantum}만큼의 자기장을 포함하는 격자 면적을 단위세포^{unit cell}로 정하면 결정 운동량 \(k\)가 잘 정의된다. 여기에 주기적인 포텐셜이 추가로 고려되면 란다우 준위는 운동량에 따라 분산하게 되고 이런 에너지 띠 구조는 일반 부도체의 에너지 띠구조와 동일하게 이해할 수 있다.

홀 전도도는 주기적인 띠구조를 가지는 부도체에서 일반적으로 양자화된 값을 가진다. \(m\)번째 에너지 띠에 해당하는 전자 파동함수를 \(u_{m}(k)\)이라고 할 때 양자화된 전도도는 아래와 같은 식으로 주어진다.

$$\sigma_{xy}=\frac{e^2}{h}\sum_{m}C_m,~~C_m=\left[\frac{1}{2\pi}\int d^2kF_m \right]$$

위 식에서 \(F_m\)은 \(m\)번째 에너지 띠의 베리 곡률^{Berry curvature}라고 불리는데, 이는 운동량 공간에 존재하는 유효자기장^{effective magnetic field}으로 파동함수의 기하학적 성질을 반영한다. 베리 곡률은 일반적으로 다음과 같은 관계를 만족시킨다.

$$F_m=\nabla\times A_m, ~~A_m=i\langle u_m |\nabla_k|u_m\rangle$$

여기서 \(A_m\)은 베리 곡률과 관련된 벡터 포텐셜을 말하고, 벡터 포텐셜은 파동함수의 운동량 공간에서의 국소 변화량에 의해 결정된다. 결국 전자 파동함수의 운동량 공간에서의 국소적인 변화는 운동량 공간의 각 점에서 국소 자기장 \(F_m\)을 형성하고 이 자기장을 브릴루앙 영역^{Brillouin zone}에서 적분한 값이 홀 전도도를 결정한다. 위에서 \(C_m\)은 \(m\)번째 에너지 띠가 만드는 베리 곡률을 모두 적분한 양으로 m번째 에너지 띠가 다른 에너지 띠와 교차하지 않으면 항상 정수로 양자화되는데, 이 정수 \(C_m\)을 천숫자^{Chern number}라고 부른다. 천숫자는 대표적인 위상 불변량으로 전자가 채워진 모든 에너지 띠의 천숫자를 모두 더한 값이 주어진 부도체의 홀 전도도를 결정한다. 전자가 채워진 에너지 띠와 비어있는 에너지 띠 사이의 에너지 갭이 유한하게 유지되는 한 홀 전도도는 항상 고정된 값을 가지게 된다.

양자 홀 상태의 경우 모든 란다우 준위가 천숫자 1을 가지기 때문에 \(N\)개의 란다우 준위가 전자로 꽉 차 있는 경우, 란다우 준위들의 천숫자 합이 \(N\)이 되고 시스템의 홀 전도도는 앞에서 본 것과 같이 \(\sigma_{xy}=N\frac{e^2}{h}\)로 주어진다.

베리 곡률의 적분값으로 주어진 천숫자가 위상 불변량이라는 사실은 수학에서 잘 알려진 비슷한 관계식인 가우스-보네트 정리^{Gauss-Bonnet theorem}와 비교를 통해서 이해해 볼 수 있다. 가우스-보네트 정리에 따르면 3차원 공간에 존재하는 2차원 폐곡면^{closed surface}의 곡률을 더한 값은 그 폐곡면이 가지는 구멍의 개수 \(g\)로 정해진다. 구의 경우는 \(g=0\)이고 도넛 형태의 폐곡면인 원환체의 경우는 \(g=1\)인데, \(g\)의 값은 각 폐곡면의 곡률이 총합과 관련된다.

이와 비슷하게 주어진 에너지 띠의 베리 곡률의 합으로 주어지는 천숫자 역시 해당 전자 파동함수가 운동량 공간에서 만드는 폐곡면이 가지는 구멍의 개수와 관련된 양이라고 할 수 있다. 천숫자가 0인 원자 부도체의 파동함수는 운동량 공간에서 구멍이 없는 구와 비슷한 폐곡면을 만들고, 천숫자가 1인 란다우 준위의 파동함수는 구멍이 하나 있는 원환체와 비슷한 폐곡면을 만든다. 원자 부도체와 양자 홀 상태는 구멍 개수가 다른 폐곡면에 해당하므로 각 폐곡면을 연속적으로 천천히 변형해서는 하나의 부도체에서 다른 부도체로 전이가 불가능하다. 각 부도체는 위상학적 안정성이 있으며, 두 부도체는 다른 위상학적 불변량을 가진다.

홀데인^Haldane 모델

위에서 언급한 양자 홀 상태의 기술을 보면, 양자 홀 상태의 위상성질에 결정적인 영향을 미치는 것은 파동함수의 베리 곡률이다. 즉, 파동함수가 운동량 공간에서 얼마만큼의 곡률을 가지고 휘어 있는지가 물질의 위상성질을 결정한다는 뜻이다. 양자 홀 상태의 초기 연구에서는 란다우 준위의 존재가 양자화된 홀 전도도 발생에 아주 중요한 역할을 하는 것으로 이해가 되었으나 위상물질에 대한 이해가 깊어지면서 양자 홀 상태가 가지는 양자화된 홀 전도도는 파동함수 자체의 특성임이 알려졌다. 이러한 결론에 다다르는데 결정적인 역학을 한 사람은 덩컨 홀데인^{Duncan Haldane} 교수다.[3]

양자 홀 효과에서 파동함수 베리 곡률의 중요성을 간파하고 있던 홀데인 교수는 간단한 격자 모델^{lattice model}을 이용해 란다우 준위 없이 양자 홀 효과가 나타나는 최초의 격자모델을 제안하였다. 좀 더 구체적으로 말하면 홀데인은 그래핀 위에 주기적인 패턴을 가지는 자기장을 도입하여 격자 모델을 구축하였다. 여기서 중요한 점은 양의 부호를 가지는 자기장과 음의 부호를 가지는 자기장이 주기적으로 나타나면서 총 자기장의 합은 영이 되어 란다우 준위는 생기지 않는다.

그래핀은 벌집구조 격자^{honeycomb lattice}를 가지는 2차원 탄소물질로 단위 격자에 두 개의 탄소원자가 들어있다. 그래핀의 저에너지 띠구조는 단위 세포 속 두 개의 격자점에 \(p_z\) 오비탈이 하나씩 놓여있는 모델로 기술이 가능하다. 단위 세포에 두 개의 오비탈이 존재하므로 격자 모델은 2Ⅹ2 행렬형태가 되고, 이런 헤밀토니안은 일반적으로 다음과 같이 적을 수 있다.

$$H({k})=h_x({k})\sigma_x+h_y({k})\sigma_y+h_z({k})\sigma_z$$

여기서 \({\sigma}_{x, y, z}\)는 파울리 행렬을 말한다. 그래핀의 저에너지 띠 구조는 원자가띠와 전도띠가 운동량 공간의 두 개의 점에서 서로 교차하는 독특한 모양을 하고 있다. 각 교차점 근방에서 운동량과 에너지의 관계를 보면, 에너지가 운동량에 대해 선형으로 증가하는 모양을 가지는데, 이런 분산 관계는 질량이 없는 상대론적 디락 방정식 ^{massless relativistic Dirac equation}으로 기술될 수 있다. 즉 그래핀의 저에너지 띠 구조는 질량이 없는 2차원 디락입자로 기술되며, 이런 이유로 에너지 띠구조의 교차점을 디락점이라고 부른다. 각 디락점 근방에서 2Ⅹ2 행렬 헤밀토니안의 모양을 보면 \(h_x({k})\)와 \(h_y({k})\)는 운동량에 선형적으로 비례하고 \(h_z({k})\)는 0이 된다.

그래핀 격자 위에 홀데인이 제안한 주기적인 자기장을 도입해서 시간역전 대칭성 ^{time-reversal symmetry}을 깨면 \(h_z({k})\)가 디락점에서 유한한 값을 가지면서 에너지 갭이 열리고, 전체 시스템은 부도체 상태가 된다. 주기적인 자기장으로 디락점에서 에너지 갭이 열리면서 갭 주변에서 큰 베리 곡률이 유도되고, 그 결과 전도띠와 원자가띠는 각각 천숫자 1, -1을 가지게 되어, 전체 시스템은 양자 홀 상태를 만들게 된다.

파동함수의 꼬임과 천숫자의 관계를 이해하는 한 가지 좋은 방법은 2Ⅹ2 행렬형태의 헤밀토니안에 해당하는 천숫자의 일반적인 형태를 확인하는 것이다. 위에서 파울리 행렬을 이용해 표현한 2Ⅹ2 행렬 헤밀토니안으로부터 원자가띠에 해당하는 파동함수를 구한 뒤, 이 파동함수의 베리 곡률을 이용해 천숫자 C를 아래와 같이 표현할 수 있다.

$$C=\frac{1}{4\pi}\int d^2k \left(\partial_{k_x}\hat{{h}}\times\partial_{k_y}\hat{{h}}\right)\cdot\hat{{h}}$$

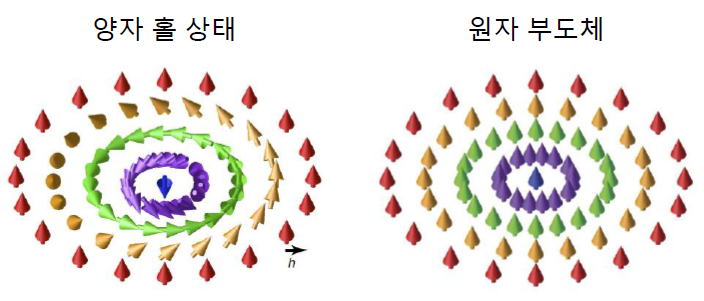
여기서 단위벡터 \(\hat{{h}}({k})\)는 \(\hat{{h}}({k})={h(k)}/|{h(k)}|\)와 같이 정의되는데, 운동량 공간의 각 점 \(k\)에서 파동함수의 방향을 나타내는 벡터이다. 천숫자 \(C\)에 대한 위의 식은 결국 단위벡터 \(\hat{{h}}({k})\)가 운동량 공간에서 가지는 입체각^{solid angle}의 총합을 \(4π\)로 나눈 값이 천숫자 \(C\)와 같다는 의미가 된다. [그림1]에서는 천숫자가 1인 양자 홀 부도체와 천숫자가 0인 원자 부도체를 기술하는 2Ⅹ2 행렬 헤밀토니안에 대한 단위벡터 \(\hat{{h}}({k})\)의 운동량 공간에서의 분포를 표현하였다. 양자 홀 부도체에서는 단위 벡터 \(\hat{{h}}({k})\)가 꼬인 구조를 가지며 총 입체각이 \(4π\)가 되고 원자 부도체에서는 단위 벡터 \(\hat{{h}}({k})\)가 큰 변화가 없이 고정된 방향을 가리키고 있고 이때 총 입체각은 0이 된다.

가장자리 금속상태: 덩치-가장자리 상관관계 ^{bulk-boundary correspondence}

위상 부도체의 가장 중요한 성질은 덩치 상태^{bulk state} 자체는 에너지 갭이 있는 부도체이지만 물질 표면^surface 혹은 가장자리^boundary에 국소화 된 금속상태가 존재한다는 사실이다.[1] 앞에서 이야기한 2차원 양자 홀 상태 물질의 가장자리를 따라 1차원 금속 상태가 존재한다. 이런 가장자리 금속 상태는 일반적으로 다른 위상 숫자를 가지는 두 부도체 사이에서 항상 나타난다. 진공 상태^{vacuum state} 역시 약한 전기장이 걸려도 전류가 흐르지 않으므로, 원자 부도체와 같이 위상성질이 없는 부도체 상태로 생각할 수 있다. 이는 곧 2차원 양자 홀 상태 물질과 진공의 경계에 나타나는 1차원 금속 역시 천숫자가 유한한 위상 부도체와 천숫자가 0인 일반 부도체 사이의 경계에 나타나는 금속 상태로 이해할 수 있다는 말이 된다.

그렇다면 양자 홀 상태와 진공(혹은 원자 부도체) 사이의 경계에는 왜 금속 상태가 존재할까? 다른 위상 숫자를 가지는 두 부도체 경계의 수직방향을 따라 한 부도체에서 다른 부도체로 천천히 움직이면서 주어진 위치에서 물질의 에너지 띠 구조가 어떻게 변해가는지를 상상해보자. 두 부도체 경계 방향을 따라서는 병진 대칭성이 존재하므로 해당 운동량이 정의될 수 있고, 이 운동량과 에너지 사이의 에너지 분산관계 및 해당 에너지 띠구조를 생각할 수 있다. 양자 홀 상태와 원자 부도체 모두 부도체이므로 원자가띠와 전도띠 사이에는 항상 유한한 에너지 갭이 존재한다.

그런데 두 부도체는 다른 위상 숫자를 가지므로 연속적인 변형을 통해 한 부도체에서 다른 부도체로 전이가 불가능하다. 즉, 두 부도체의 경계면에서 불연속적인 변화가 나타나야 한다는 말이며, 이는 경계면에서 에너지 갭이 0이 되면서 금속 상태가 나타나야 한다는 뜻이 된다. 얼핏 들으면 아주 단순한 설명인데, 놀랍게도 위에서 설명한 아이디어는 위상 성질이 다른 두 부도체 경계에서 금속 상태가 나타나는 원인을 아주 일반적으로 잘 설명해준다.

2차원 양자 홀 상태 물질의 가장자리를 따라 1차원 금속 상태가 나타나는 것과 비슷하게, 3차원 위상물질의 표면에는 2차원 금속 상태가 나타나고, 1차원 위상물질 가장자리에는 0차원 금속 상태가 나타난다. 일반적으로 \(d\)차원(\(d\)는 자연수) 위상 부도체의 \(d-1\)차원 표면에는 금속 상태가 나타나는데 이렇게 \(d\)차원 위상 숫자와 \(d-1\)차원 표면 금속 상태의 상관관계를 덩치-가장자리 상관관계^{bulk-boundary correspondence}이라고 부르며, 이는 위상 물질의 가장 중요한 특징 중 하나다.

위상물질 가장자리 금속 상태는 물질의 차원 및 해당 위상 숫자의 종류에 따라 다른 성질을 가진다. 예를 들어, 양자 홀 상태의 1차원 가장자리 금속은 한쪽 방향으로만 움직일 수 있는데, 이로 인해, 해당 금속 상태는 카이랄 경계 상태^{chiral edge state}라고 불린다. 카이랄 경계 상태는 천숫자를 가지는 2차원 부도체의 고유한 성질로 천숫자의 부호가 카이랄 상태가 움직이는 방향을 결정하고, 천숫자의 크기가 카이랄 경계 모드의 개수를 결정한다. 천숫자가 아닌 다른 위상 숫자를 가지는 위상 부도체에서는 해당 가장자리 금속상태의 성질이 일반적으로 다른데, 이와 관련해서는 아래에서 좀 더 자세히 이야기하고자 한다.

시간 역전 불변성과 양자 스핀 홀 부도체 ^{Time-reversal symmetry and quantum spin Hall insulator}

2차원 양자 스핀 홀 부도체^{quantum spin Hall insulator}의 이론적 예측과 실험적 발견은 고체의 에너지띠 구조를 이해하는 방식에 근본적인 변화를 가져왔다. 양자 스핀 홀 상태는 양자 홀 상태와 마찬가지로 덩치상태 자체는 에너지 갭이 있는 부도체지만 물질 가장자리를 따라 전류가 흐르는 상태를 말한다.[4] 양자 홀 상태와는 달리 양자 스핀 홀 상태는 시간 역전 대칭성^{time-reversal symmetry}를 만족시킨다. 뿐만 아니라 가장자리 금속상태는 업-스핀^up-spin 전자와 다운-스핀^down-spin 전자가 반대방향으로 움직이고 있는데, 이런 1차원 금속 상태를 나선형 금속 상태^{helical metallic state}라고 한다. 이런 양자 스핀 홀 부도체의 발견은 양자 홀 상태를 넘어서는 새로운 위상 상태의 존재를 확인했다는 점에서 중요할 뿐만 아니라 대칭성이 보호하는 위상학적 상태^{symmetry protected topological states}라는 새로운 개념이 도입되는 계기가 되었는데, 이는 향후 다양한 위상학적 결정 물질^{topological crystalline material}의 발견으로 이어졌다.

양자 스핀 홀 효과에 대한 연구는 전기장을 통해 전자의 스핀 수송현상을 제어하려는 스핀트로닉스^spintronics 연구의 발전에 그 근본을 두고 있다. 전자는 전하와 더불어 스핀을 가지고 있는데, 자기장을 걸어서 업-스핀을 가진 전자와 다운-스핀을 가진 전자를 반대 방향으로 움직이게 만들면 전하의 수송 없이 스핀만의 수송이 가능하다.

2차원 양자 스핀 홀 부도체를 구현하는 가장 간단한 방법은 업-스핀 전자로 구성된 양자 홀 상태와 다운-스핀 전자로 구성된 양자 홀 상태를 겹쳐놓는 것이다. 여기서 중요한 점은 두 개의 양자 홀 상태의 천숫자가 크기는 같지만 부호가 반대가 되어, 전체 시스템의 천숫자는 0이 되어야 한다. 천숫자 총합이 0인 경우에는 전체 시스템이 시간 역전 대칭성^{time-reversal symmetry}을 가질 수 있다. 각각의 양자 홀 상태를 구현하려면 자기장을 걸어야 하지만, 업-스핀 양자 홀 상태와 다운-스핀 양자 홀 상태에 걸린 자기장 방향이 반대면, 전체 자기장은 0이 되어서 시간 역전 대칭성이 유지된다. 두 번째로 중요한 점은 각 전자의 스핀 방향이 보존이 되어야 한다는 것이다. 즉 업-스핀 전자와 다운-스핀 전자는 각자의 스핀 방향을 유지한 채 운동해야 한다.

이론적으로는 간단하지만 실제로 위에서 언급한 방식으로 양자 스핀 홀 부도체를 구현하려면, 스핀에 따라 자기장 방향을 반대로 걸어주어야 하는 어려움이 있다. 그런데 재미있게도 자연계에서는 이런 스핀 방향에 의존하는 자기장을 걸 수 있는 아주 자연스러운 방법이 있다. 바로 스핀-궤도 결합^{spin-orbit coupling}을 이용하는 것이다. 스핀-궤도 결합은 일반적으로 아래와 같은 식으로 표현할 수 있다.

$$H_{SOC}=-\alpha\vec{S}\cdot(\vec{p}\times\vec{E})=-\vec{S}\cdot\vec{B}_{eff}$$

여기서 \(\vec{S}, \vec{P}, \vec{E}\)는 각각 전자의 스핀, 운동량, 그리고 외부 전기장을 말한다. \(\alpha\)는 스핀-궤도 결합의 크기를 나타내는 상수이고 \(\vec{B}_{eff}\) 스핀-궤도 결합이 만드는 유효자기장을 말한다. 만약 2차원 물질이 \(xy\)평면에 놓여있다고 하고 전기장이 \(y\)방향, 전자의 운동방향이 \(x\)방향이라고 하면 유효 자기장은 \(z\)방향을 향한다. 이때 업-스핀 전자와 다운-스핀 전자는 반대 부호의 스핀 각운동량을 가지므로 해당 유효자기장의 방향도 반대가 된다. 스핀 방향에 의존하는 자기장이 걸린 것이다. 물론 엄밀한 의미에서 전기장이 상수인 경우 스핀-궤도 결합은 란다우 준위를 만들지 못한다. 격자 변형을 통해 전기장이 실공간 위치에 따라 변화해야, 진정한 의미에서 스핀 방향에 의존하는 란다우 준위가 생길 수 있다. 하지만 스핀-궤도 결합이 스핀에 의존하는 유효 자기장을 줄 수 있다는 사실은 일반적으로 성립한다. 또한 위의 헤밀토니안은 스핀 각운동량의 z성분을 보존하므로 업-스핀과 다운-스핀이 서로 섞이지 않게 된다.

양자 스핀 홀 부도체를 기술하는 최초의 모델 헤밀토니안인 케인-멜레^Kane-Mele 모델은 케인^Kane 교수와 멜레^Mele 교수가 제안했는데, 기본적으로 위에서 설명한 아이디어를 기반으로 한다. 좀 더 구체적으로 말하면 양자 홀 부도체를 기술하는 홀데인  모델을 업-스핀, 다운-스핀 전자에 대해서 따로 정의한 뒤에, 두 개의 홀데인 모델을 스핀-궤도 결합을 통해 연결한 것이 바로 케인-멜레의 양자 스핀 홀 부도체 모델이다.

양자 스핀 홀 부도체 역시 가장자리에 1차원 금속 상태를 가진다. 이 가장자리 금속 상태의 성질은 양자 스핀 홀 상태를 구성하는 두 개의 양자 홀 부도체의 가장자리 상태를 기반으로 이해할 수 있다. 예를 들어, 업-스핀 전자가 만드는 양자 홀 상태의 천숫자가 +1이고 다운-스핀 전자가 만드는 양자 홀 상태의 천숫자가 -1이며, 이 둘을 결합해서 양자 스핀 홀 상태가 만들어졌다고 하자. 천숫자를 고려하면 업-스핀 전자의 양자 홀 상태는 경계를 따라 시계 방향으로 움직이는 카이랄 모드를 가져야 하고, 다운-스핀 전자의 양자 홀 상태는 같은 경계를 따라 반시계 방향으로 움직이는 카이랄 모드를 가져야 한다. 두 가지 카이랄 모드의 집합이 바로 양자 스핀 홀 부도체의 나선형 가장자리 모드가 된다.

위에서 설명한 방식으로 양자 스핀 홀 부도체와 나선형 가장자리 금속 상태를 이해하려면 스핀 각운동량의 \(z\)성분이 보존되어야 한다. 이 경우 업-스핀 전자와 다운-스핀 전자 사이에 상호작용이 없게 되고, 각 스핀이 만드는 양자 홀 상태도 독립적인 상태로 유지가 될 수 있다. 하지만 실제 물질에서 스핀-궤도 결합의 모양은 훨씬 더 복잡하고, 일반적으로 스핀 각운동량은 보존되지 않는다. 이 말은 실제 물질에서는 업-스핀 전자와 다운-스핀 전자 사이에 상호 작용이 있다는 말이다.

이런 스핀 사이의 상호 작용이 허용된 경우 나선형 가장자리 모드가 안정하게 존재할 수 있을까 하는 의문이 생길 수 있다. 주어진 모서리에서 양의 속도^{positive velocity}를 가지고 움직이는 업-스핀 전자의 가장자리 모드와 음의 속도^{negative velocity}를 가지고 움직이는 다운-스핀의 가장자리 모드의 에너지 분산관계를 보면, 두 개의 모드가 운동량-에너지 공간에서 서로 교차할 수 있다. 여기서 만약 다른 스핀 사이의 상호작용이 존재하면 교차점에서 에너지 갭이 열리면서, 가장자리 금속 상태가 없어질 가능성이 있기 때문이다. 하지만 재미있게도 실제 양자 스핀 홀 부도체에서는 스핀 각운동량이 보존되지 않는 상황에서도 나선형 가장자리 상태가 안정되게 존재할 수 있는데, 이는 양자 스핀 홀 시스템이 시간 역전 대칭성을 갖기 때문에 가능하다.

시간 역전 대칭성과 나선형 가장자리 상태의 안정성 사이의 관계에 대해 좀 더 자세히 알아보자. 시간 역전 대칭성을 나타내는 연산자^operator를 \(T\)라고 하자. 전자와 같이 스핀 \(1/2\)을 가지는 페르미온의 중요한 성질은 시간 역전 대칭성을 두 번 가했을 때 파동함수에 마이너스 부호가 붙게 된다는 것이다. \(T\) 연산자를 이용하면 이는 \(T^2=-1\)로 표시된다. 이 경우 임의의 파동함수 \(\varphi\)와 그 시간 역전 파트너인 \(T\varphi\)이 반드시 같은 에너지를 가지는 독립적인 상태가 된다. 이렇게 시간 역전 대칭성이 있는 전자계에서 같은 에너지를 가지는 두 개의 독립적인 파동함수가 반드시 짝을 이뤄 존재한다는 사실을 크래머스 정리^{Kramers theorem}라고 부른다.

크래머스 정리는 시간 역전 대칭성이 있는 전자계의 에너지 띠 구조에 중요한 축퇴^degeneracy 조건을 준다. 양자 스핀 홀 부도체의 1차원 가장자리를 따라서 병진 대칭성이 존재하므로 가장자리 방향의 운동량 \(k\)가 정의될 수 있고, 시스템의 에너지는 운동량 공간에서 \(2π\)의 주기를 가지고 반복이 된다. (가장자리 방향의 격자 상수를 편의상 1이라고 하자.) 시간 역전 대칭성에 대해 운동량 \(k\)는 \(-k\)와 대응한다. 즉 운동량 \(k\)를 가지는 파동함수 \(\varphi(k)\)의 시간 역전 파트너 \(T\varphi(k)\)는 운동량 \(-k\)를 가진다는 말이다.

그런데 운동량 \(k\)가 0 혹은 \(π\)값을 가질 경우 \(k\)와 \(-k\)가 같으므로(운동량 공간에서는 에너지띠 구조가 \(2π\) 주기를 가지고 반복된다는 점을 기억하자), 이 두 점에서는 \(\varphi(k)\)와 \(T\varphi(k)\)가 같은 운동량과 같은 에너지를 가지며 축퇴되어 있어야 한다. 이런 현상을 크래머스 축퇴^{Kramers degeneracy}라고 부르고, \(k=0 \)와 \(k= π\) 두 운동량을 시간 역전 불변 운동량^{time-reversal invariant momentum}이라고 부른다. \(k=0\)에 있는 크래머스 짝들^{Kramers pairs}과 \(k= π\)에 있는 크래머스 짝들을 이어주는 에너지 분산 방식은 [그림3]처럼 크게 두 가지 형태로 구분된다.

첫 번째 경우는 \(k=0\)에 있는 크래머스 짝들이 \(k=0\)에서 벗어나면서 살짝 갈라졌다가 \(k= π\)에서 다시 크래머스 짝을 이룬다. 반면 두 번째 경우에는 \(k=0\)에 있는 크래머스 짝들이 \(k=0\)에서 벗어나면서 갈라졌다가 \(k= π\)에서는 다른 에너지띠와 새로운 크래머스 짝을 이룬다. 절대 영도에서 전자가 찬 에너지띠와 비어있는 에너지띠의 에너지 경계를 페르미 준위^{Fermi level}라고 하는데, 첫 번째 경우는 \(k=0\)와 \(k= π\) 사이에서 페르미 준위와 에너지띠 사이에 짝수 개의 교차점이 존재하고, 두 번째 경우는 홀수 개의 교차점이 존재한다. 또한 첫 번째 경우에는 에너지 띠를 연속적으로 변형시키면서 페르미 준위를 지나는 에너지띠가 없는 부도체의 밴드구조를 만들 수 있는 반면에 두 번째 경우에는 에너지띠가 항상 연속적으로 연결되어 있고, 에너지 갭이 절대로 나타나지 않는다. 첫 번째 경우가 원자 부도체와 같이 위상성질이 없는 부도체에 해당하고 두 번째 경우가 가장자리에 나선형 금속 상태를 가지는 양자 스핀 홀 부도체에 해당한다. 시간 역전 대칭성이 있는 부도체가 두 가지 형태로 구분된다는 사실을 좀 더 전문적인 용어로 “위상 숫자가 \(Z_2\)값을 가진다” 라고 표현한다. \(Z_2=0\)이면 일반 부도체, \(Z_2=1\)이면 양자 스핀 홀 부도체가 된다.

3차원 위상학적 부도체^{Three-dimensional topological insulator}

2차원 양자 스핀 홀 부도체의 발견은 바로 3차원 위상 부도체의 예측 및 발견으로 이어졌다.[5] 3차원 위상 부도체 역시 2차원 표면에 금속 상태를 가진다. 3차원 위상 부도체의 2차원 표면을 따라 병진 대칭성이 있는 경우, 표면 2차원 브릴루앙 영역^{Brillouin zone}의 에너지 띠구조를 생각해보자. 일반적으로 2차원 브릴루앙 영역에는 4개의 시간역전불변 운동량이 존재하는데 이 네 개의 운동량을 각각 \(\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\)라고 하자. 각 \(\Gamma_{i=1,2,3,4}\)에서 에너지띠들은 크래머스 짝을 이루고 있고, 이 점에서 벗어나면 스핀-궤도 결합 때문에 크래머스 짝들은 에너지가 따른 두 개의 상태로 나뉜다. 결국 각 \(\Gamma_i\)에서 크래머스 짝들은 2차원 디락점을 만들게 된다. 2차원 양자 스핀 홀 부도체의 가장자리 에너지띠 구조를 설명할 때 두 개의 시간역전불변 운동량 (\(k=0\)와 \(k= π\)) 사이에서 크래머스 짝들 사이의 연결관계를 두 가지로 분류할 수 있다고 설명했다. 마찬가지로 3차원 위상 부도체 표면에 있는 네 개의 \(\Gamma_i\)중 임의의 두 점 사이의 에너지띠 구조 역시 두 가지로 구분이 가능하다.

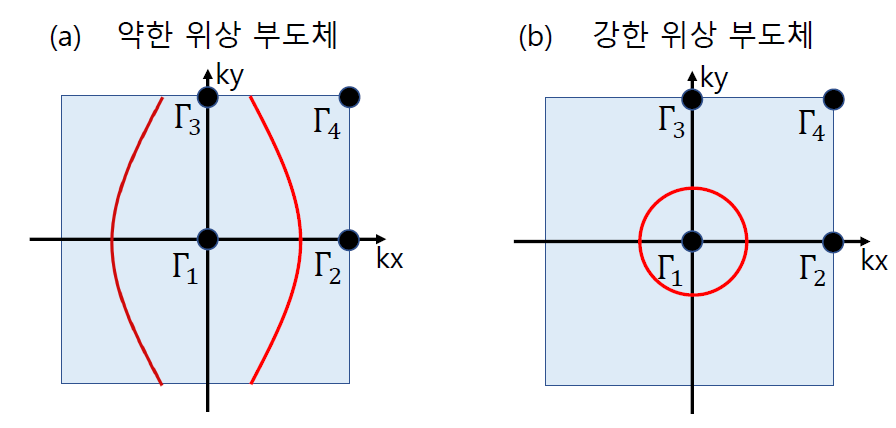
우선 [그림4-a]의 페르미 표면^{Fermi surface} 구조를 보자. 여기서는 \(\Gamma_1\)과 \(\Gamma_2\)사이, 그리고 \(\Gamma_3\)와 \(\Gamma_4\)사이의 밴드구조가 모두 [그림3-b]와 같은 구조를 가지고 있다. 왜냐하면 두 시간 역전 불변 운동량 사이에서 페르미 준위를 지나는 표면 상태가 홀수 개 있기 때문이다. 이러한 형태의 밴드 구조는 2차원 양자 스핀 홀 부도체를 2차원 물질의 수직방향으로 겹쳐 쌓으면 만들 수 있다. 각 2차원 물질의 가장자리가 [그림3-b]와 같은 밴드구조를 가지므로 이런 밴드구조를 수직방향으로 반복하면 [그림4-a]과 같은 표면 금속 상태를 가지는 3차원 부도체 상태를 만들 수 있다. 이런 방식으로 2차원 양자 홀 부도체를 수직방향으로 겹겹이 쌓아서 만든 3차원 위상 물질을 약한 위상 부도체^{weak topological insulator}라고 한다.

이런 층상 구조로 기술되는 3차원 부도체 역시 \(Z2\) 위상 숫자 \(ν\)로 특징지을 수 있는데, \(ν=0\)는 2차원 일반 부도체를, \(ν=1\)은 2차원 양자 스핀 홀 부도체를 겹겹이 쌓아서 만든 약한 위상 부도체를 가리킨다. 2차원 물질을 겹겹이 쌓아서 3차원 구조를 만드는 방법은 쌓는 방향에 따라 크게 세 가지가 있다. 즉 \(xy\)평면과 평행한 2차원 물질들을 \(z\)방향으로 쌓거나, \(yz\)평면과 평행한 구조를 \(x\)방향으로, 혹은 \(zx\)평면과 평행한 구조를 \(y\)방향으로 쌓는 것이 그것이다. 각각의 경우에 해당하는 \(Z2\) 위상 숫자를 \(ν_1, ν_2, ν_3\)라고 하겠다.

3차원 약한 위상 부도체 표면의 경우 주어진 \(\Gamma_i\)와 이웃한 \(\Gamma_j\)사이의 밴드구조는 \(\Gamma_j\)를 어떻게 잡는지에 따라 \(Z2=0\) 형태일 수도 있고 \(Z2=1\)형태일 수도 있다. 즉 [그림4-a]의 경우 \(\Gamma_1\)과 \(\Gamma_2\)사이, 그리고 \(\Gamma_1\)과 \(\Gamma_4\)사이의 밴드구조는 \(Z2=1\)형태이지만 \(\Gamma_1\)과 \(\Gamma_3\) 사이에는 \(Z2=0\)형태의 밴드 구조를 가진다. 그렇다면 주어진 \(\Gamma_i\)에서 이웃한 \(\Gamma_j\) 사이의 밴드 구조가 모두 \(Z2=1\)형태일 수는 없을까? 그러한 표면 밴드구조를 가지는 위상물질을 강한 위상 부도체^{strong topological insulator}라고 부른다. 강한 위상부도체의 페르미 표면은 홀수 개(하나 혹은 세 개)의 2차원 다락점을 감싸고 있는데, 이는 페르미 표면이 짝수개의 표면 디락점을 감싸는 약한 위상 부도체와 구분이 된다. 이런 강한 위상 부도체의 위상 상태를 기술하는 \(Z2\) 위상숫자를 \((ν_0)\)라고 하자. 결국 시간 역전 대칭성이 있는 3차원 부도체는 \((ν_0, ν_1, ν_2, ν_3)\) 이렇게 네 개의 \(Z2\) 위상 숫자를 기반으로 위상학적으로 분류될 수 있다.

결정 대칭성과 위상학적 결정 부도체^{topological crystalline insulator}

위에서 시간 역전 대칭성이 있는 물질에서 나타날 수 있는 2차원, 3차원 위상 부도체에 대해서 살펴보았다. 시간 역전 대칭성은 고체에서 아주 흔히 존재하는 대칭성이다. 그런데 고체 물질은 시간 역전 대칭성 말고도, 다양한 결정 대칭성^{crystalline symmetry}을 가진다. 자성이 없는 3차원 고체 결정은 230개의 공간군 대칭성^{space group symmetry}을 가진다. 그렇다면 시간 역전 대칭성 대신 결정 대칭성 때문에 나타나는 위상 부도체 상태는 존재하지 않는지를 물을 수 있다.

이 질문에 대한 첫 번째 답은 리앙 푸^{Liang Fu} 교수에 의해 주어졌다.[6] 리앙 푸 교수는 격자의 회전 대칭성에 의해서 보호되는 3차원 위상 부도체가 존재함을 이론적으로 보였고, 이렇게 격자 대칭성이 보호하는 위상 부도체를 위상학적 결정 부도체^{topological crystalline insulator}라고 명명했다. 하지만 회전대칭성이 보호하는 위상학적 결정 부도체는 아직 발견되지 않았다. 실험적으로 발견된 최초의 위상학적 결정 부도체는 거울대칭성^{mirror symmetry}에 의해 보호되는 위상 부도체 상태인데,[7] 이에 대해서 좀 더 자세히 알아보자.

우선 거울대칭성이 보호하는 2차원 위상 부도체를 생각해보자. 2차원 물질이 \(xy\) 평면에 놓여있다고 하고, 이 물질이 \(xy\) 평면에 대한 거울 대칭성을 가진다고 하자. 해당 거울 대칭 연산자를 \(Mz\)라고 하면, \(Mz\)는 공간 좌표 \((x,y,z)\)를 \((x,y,-z)\)로 뒤집어 준다. 스핀-궤도 결합이 있는 전자계에서 \(Mz\)는 전자의 공간 좌표뿐만 아니라 스핀 방향에도 작용을 하는데, 스핀의 \(z\) 성분은 \(Mz\)에 대해서 불변이지만 \(x, y\)성분은 \(Mz\)에 대해 부호가 바뀐다. 즉 스핀의 \(x,y,z\) 성분을 \(Sx, Sy, Sz\)라고 하면 \(Mz\)에 대해서 \((Sx,Sy,Sz)\)가 \((-Sx,-Sy,Sz)\)와 같이 바뀐다. 각 성분의 부호 변화는 공간좌표의 경우와 정확히 반대로 바뀌는데, 이는 스핀 각운동량이 축성 벡터^{axial vector}라는 사실에 기인한다. 또한 \((Mz)^2=-1\) 을 만족하는데, 이는 시간 역전 연산자 \(T\)의 경우와 마찬가지로 스핀 \(1/2\)인 입자가 360도 회전할 때 해당 파동함수의 부호가 바뀐다는 사실 때문에 나타난다. \((Mz)^2=-1\)는 곧 \(Mz\)의 고유값이 \(+i\) 혹은 \(-i\)라는 뜻이 된다.

\(Mz\)가 \((x, y)\) 좌표를 바꾸지 않는다는 말은 곧 2차원 물질의 운동량 \((kx, ky)\)도 \(Mz\)에 대해서 불변이라는 말이 된다. 따라서 운동량 공간의 각 점에서 파동함수들은 \(Mz\) 연산자의 고유 벡터^eigenvector가 될 수 있다. \(Mz\) 고유값이 \(+i\)인 에너지띠들과 \(Mz\) 고유값이 \(-i\)인 에너지띠들이 독립적으로 존재하므로, 각 에너지띠 집합들마다 천숫자를 따로 정의할 수 있다. \(C_{+i}, C_{-i}\)를 각각 페르미 준위 아래에 있는 에너지띠 중에서 \(Mz\) 고유값이 \(+i\), \(-i\)인 에너지띠들의 천숫자라고 정의하자. 편의상 페르미 준위 아래에 있는 에너지띠들의 전체 집합을 원자가띠라고 하고, 페르미 준이 위에 있는 에너지띠들의 전체 집합을 전도띠라고 하자. 그러면 원자가띠 전체의 총 천숫자는 \(C=C_{+i} + C_{-i}\)로 주어지는데, \(C\)가 0이 아니면 시스템은 양자 홀 부도체가 된다. 이 시스템에서는 총 천숫자 \(C\)말고 거울 천숫자^{mirror Chern number} \(C_{M}=[C_{+i}-C_{-i}]/2\)라는 새로운 위상 숫자도 정의될 수 있다. 총 천숫자가 0이고 거울 천숫자가 0이 아닌 2차원 부도체를 거울 대칭성이 보호하는 2차원 위상학적 결정 부도체^{topological crystalline insulator protected by mirror symmetry}라고 부른다. 이 시스템의 1차원 가장자리 브릴루앙 영역에는 거울 천숫자만큼의 1차원 디락점이 나타나고, 표면 금속 상태를 만들어준다.

위에서 설명한 위상학적 결정 부도체의 개념은 3차원으로도 확장될 수 있다. \(Mz\) 연산자는 \(z\)성분 운동량 \(kz\)의 부호를 바꾸지만, \(kz=0\) 와 \(kz= π\)에 해당하는 2차원 브릴루앙 영역은 각각 \(Mz\)에 대해서 불변이므로, 이 두 평면상에서는 에너지띠들의 거울 천숫자를 2차원에서와 마찬가지로 정의할 수 있다. 시간 역전 대칭성이 있는 3차원 부도체 중 \(kz=0\) 혹은 \(kz= π\) 두 평면 중 어느 하나에서라도 거울 천숫자가 0이 아닌 부도체를 \(Mz\) 거울 대칭성이 보호하는 3차원 위상학적 결정 부도체라고 부른다. 흥미롭게도 SnTe이라는 반도체가 거울 대칭성이 보호하는 3차원 위상학적 부도체라고 2012년에 이론적으로 제안이 되었고, 바로 그다음 해에 실험적으로 증명이 되었다.

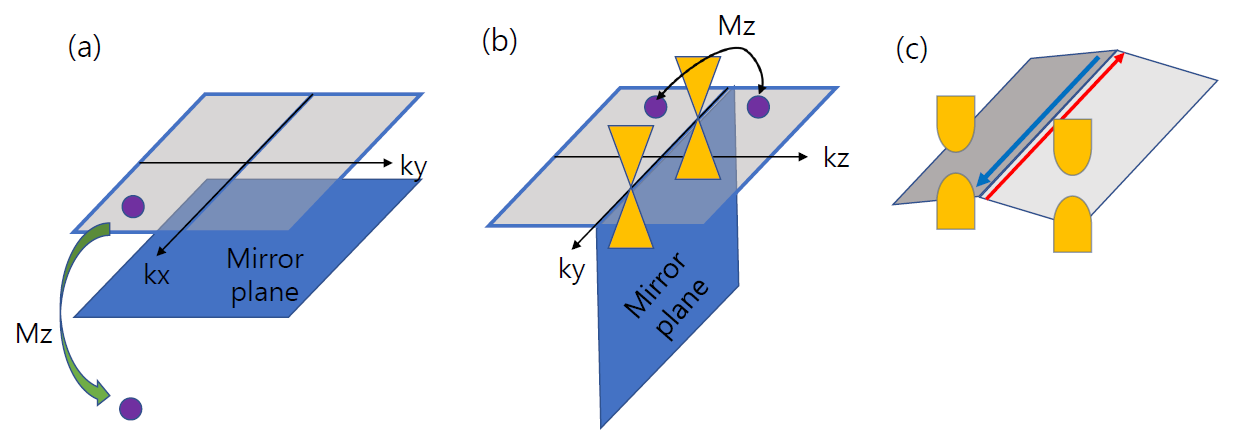
거울대칭성이 보호하는 위상학적 결정 부도체가 실험적으로 확인될 수 있었던 것은 바로 이 시스템이 가지는 독특한 표면 금속상태 때문이다. 앞에서 이야기한 시간 역전 불변성이 보호하는 3차원 위상부도체의 경우 물질의 표면이 어떤 방향을 향하고 있는지에 상관없이 항상 2차원 금속 상태가 존재한다. 반면 위상학적 결정 부도체의 경우는 표면의 방향에 따라 금속 상태가 나타날 수도 있고, 그렇지 않을 수도 있다. 예를 들어, \(Mz\) 거울 대칭성이 보호하는 위상학적 결정 부도체의 경우 \(xy\) 평면에 평행한 표면의 경우에는 표면에서 거울 대칭성이 깨져있는데, 이 경우는 일반적으로 표면 금속 상태가 나타나지 않는다.([그림5-a]) 반면 [그림5-b]처럼 표면이 \(yz\) 평면 혹은 \(xz\) 평면에 평행한 경우는 표면에서도 \(Mz\) 대칭성이 유지되고, 이 경우는 표면 금속 상태가 나타난다.

좀 더 구체적으로 [그림5-b]처럼 \(yz\) 평면에 평행한 표면을 생각해보자. 표면 브릴루앙 영역의 임의의 운동량 \((ky, kz)\)는 \(Mz\) 거울 대칭성에 대해 \((ky,-kz)\)로 대응이 된다. 이 말은 \(kz=0\)와 \(kz= π\)인 \(ky\) 방향 직선위의 운동량은 \(Mz\)에 대해 불변이고, 이 직선 위에서 에너지 띠들은 \(Mz\) 대칭성의 고유값을 가질 수 있다. 사실 이 두 직선은 \(Mz\)에 대해 불변인 2차원 브릴루앙 영역인 \(kz=0\) 혹은 \(kz= π\) 평면의 가장자리에 해당한다. 만약 브릴루앙 영역인 \(kz=0\) 혹은 \(kz= π\) 평면이 0이 아닌 거울 천숫자를 가지게 되면, \(yz\) 평면의 표면 브릴루앙 영역에서 \(kz=0\) 혹은 \(kz= π\) 직선 위에 2차원 디락점이 나타나고, 표면 금속 상태가 나타난다. 이렇게 표면 방향에 따라 표면 금속상태 혹은 표면 디락점 상태의 분포가 달라지는 점을 이용해서 SnTe가 거울대칭성이 보호하는 3차원 위상학적 결정 부도체임이 실험적으로 증명될 수 있었다.

고차 위상 부도체^{Higher order topological insulator}

지금까지 이루어진 위상학적 부도체에 대한 논의를 보면, 위상 부도체는 공통적으로 양자화된 위상 숫자로 특징지어지고, 물질 표면에 금속 상태를 가지고 있다. 특히 후자의 경우는 덩치-가장자리 상관관계^{bulk-boundary correspondence}라고 불리며 2차원 위상 부도체의 1차원 가장자리, 3차원 부도체의 2차원 가장자리에 금속상태가 반드시 존재해야 한다는 중요한 특징을 기술한다. 일반적으로 \(d\)차원의 위상 부도체는 \(d-1\)차원의 표면 금속상태를 가진다.

하지만 최근 들어 이런 전형적인 덩치-가장자리 상관관계를 넘어서는 새로운 위상 부도체가 발견되었다. 그 중 대표적인 예가 고차 위상 부도체^{higher-order topological insulator}이다.[8] 3차원 고차 위상 부도체의 2차원 표면은 에너지 갭이 있는 부도체이지만, 두 표면이 만나는 1차원 모서리^hinge를 따라서 카이랄 금속 상태 혹은 나선형 금속 상태가 나타난다. 즉 \(d\)차원의 위상 부도체의 \(d-1\)차원 가장자리는 부도체 상태이고, \(d-2\)차원 가장자리에 금속 상태가 나타나는 것이다. 이런 고차 위상 부도체의 존재는 결정대칭성이 보호하는 위상 부도체의 독특한 성질이다.

고차 위상 부도체를 얻는 한 가지 간단한 방법을 설명하기 위해, 위에서 언급한 \(Mz\) 거울 대칭성이 보호하는 3차원 위상학적 결정 부도체를 생각해보자. 앞에서 설명한 대로 이 물질의 \(yz\) 표면은 \(Mz\) 대칭성이 있고, \(kz=0\) 혹은 \(kz= π\) 직선 위에 거울 천숫자 만큼의 2차원 디락점을 가지는 금속 상태이다.([그림5-b]) 이 상태에서 [그림5-c]처럼 \(yz\) 표면을 \(Mz\) 대칭성을 유지하면서 살짝 구부려보자. 이때 주의할 점은 구부러진 구조의 양쪽 표면 사이의 경계인 1차원 모서리는 여전히 \(Mz\) 대칭성에 대해 불변이고, \(Mz\) 대칭성이 구부러진 구조의 한쪽 면을 다른 쪽 면으로 대응시켜서 전체 구부러진 구조는 \(Mz\) 대칭성을 유지하는 것이다.

이때 구부러진 구조의 각 면에서는 \(Mz\) 대칭성이 깨진다. \(Mz\)가 하나의 면을 다른 면으로 대응시킨다는 점은 각각의 면에서는 \(Mz\) 대칭성이 깨졌다는 말이 된다. 이 경우 \(Mz\) 대칭성이 보호하는 위상학적 결정 부도체의 일반적인 성질에 의하면 \(Mz\) 대칭성이 깨진 각 면은 [그림5-a])처럼 부도체 상태가 되어야 한다. 하지만 두 면이 맞닿은 1차원 모서리를 따라서는 \(yz\) 평면을 구부리는 변형과정에서 계속 \(Mz\) 대칭성이 유지되므로 모서리 위에 존재하던 1차원 나선형 금속 상태가 계속 존재한다. 1차원 나선형 금속 상태는 \(Mz\) 거울 대칭성에 의해서 보호된다. 이렇게 하여 \(Mz\) 대칭성을 가지는 3차원 부도체가 1차원 모서리를 따라서 나선형 금속 상태를 가지는 고차 위상 부도체가 만들어진다.[8]

위의 설명을 보면 거울대칭성이 보호하는 위상학적 결정 부도체의 경우 유한한 크기의 3차원 구조를 만들 때 표면방향을 어떻게 만드는지에 따라 2차원 표면 금속상태가 생길 수도 있고, 모서리를 따라 1차원 금속 상태가 나타날 수 있다. 이런 이유로 위에서 이야기한 바와 같이 위상학적 결정 부도체로 확인된 SnTe가 고차 위상 부도체의 후보 물질로도 제안되었다. 고차 위상 부도체의 이론적인 제안은 그 후 새로운 위상물질 상태에 대한 많은 연구로 이어졌고, 현재는 모든 고차 위상 부도체의 종류와 각 위상상태를 보호하는 결정 대칭성에 대한 체계적인 분류가 이루어졌다. 실험적으로는 비스무스 (Bi) 결정이 1차원 나선형 금속상태를 모서리에 가지는 최초의 고차 위상 부도체임이 증명되었다. 이 물질의 고차 위상 성질은 시간 역전 대칭성과 3중 회전 대칭성, 그리고 공간 반전 대칭성에 의해 보호된다.

가로막힌 원자 부도체^{obstructed atomic insulator} 및 전기 다중극 모멘트 부도체^{electric multipole insulator}

고차 위상 부도체의 발견으로 \(d\)원 부도체 중 \(d-1\) 차원의 표면 금속 상태를 가지는 기존의 위상 부도체를 1차 위상 부도체, \(d-2\) 차원의 표면 금속 상태를 가지는 새로운 위상부도체를 2차 위상 부도체 등으로 구분해서 부르기 시작했다. 앞에서 언급한 1차원 모서리 금속 상태를 가지는 3차원 위상 부도체는 3차원 2차 부도체이다. 그렇다면 모서리와 모서리가 만나서 생기는 꼭지점에 0차원 금속 상태를 가지는 3차원 3차부도체도 가능한가 하는 질문을 해볼 수 있다.

사실 이렇게 0차원 꼭지점에 금속상태가 나타나는 위상학적 결정 부도체는 위에서 언급한 고차 위상 부도체가 발견되기 조금 더 전에 이론적으로 제안되었다. 0차원 꼭지점 금속상태는 3차원 3차 부도체뿐만 아니라 2차원 2차 부도체, 1차원 1차 부도체에서도 존재한다. 2차원 양자 홀 부도체와 양자 스핀 홀 부도체는 1차원 가장자리 금속을 가지므로 2차원 1차 위상 부도체에 해당하고, 2차원 2차 부도체는 모서리 두 개가 만나는 꼭지점에 금속 상태를 가진다. 1차원 물질의 경우는 가장자리가 원래 0차원이므로 1차원 1차 부도체 자체가 0차원 꼭지점 금속상태를 가진다.

0차원 가장자리 금속상태를 가지는 1차원 위상 부도체는 다음과 같은 방법으로 이해할 수 있다. 원자핵과 전자 1개로 구성된 원자를 규칙적으로 정렬하여 1차원 격자구조를 만들자. 이렇게 만들어진 원자 부도체는 자연스럽게 \(Mx\) 거울 대칭성을 가진다. 여기서 \(Mx\)는 \(x\)좌표를 \(-x\)로 보내는 거울 대칭 연산을 말한다. 그런데 이웃한 원자 사이의 상호작용, 혹은 전자 구름 사이의 겹침을 고려하면, \(Mx\) 대칭성을 만족하는 새로운 형태의 1차원 부도체 상태를 생각할 수 있다. 즉, 각 원자핵에 속박되어 있던 전자가 이웃한 원자핵의 중간 지점에 존재하는 상태가 그것이다.([그림6-a] 참고) 결국 \(Mx\) 대칭성을 만족하는 1차원 부도체는 두 가지가 가능하다. 주어진 원자핵과 가장 가까이 있는 전자 사이의 거리를 기준으로 전기 분극^{electric polarization} \(P\)를 정의한다면, 전자가 원자핵과 같은 위치에 있는 부도체는 \(P=0\), 전자가 이웃한 원자핵 사이에 존재하면 \(P=1/2\)이 된다. 여기서 이웃한 원자핵 사이의 거리를 1이라고 가정했다. 결국 \(Mx\) 대칭성을 가지는 1차원 격자의 전기분극은 \(P=0, P=1/2\) 이렇게 두 가지로 구분이 된다. 이때 후자가 바로 0차원 가장자리 금속상태를 가지는 1차원 위상 부도체가 된다.

\(Mx\) 대칭성이 있는 1차원 부도체를 좀 더 조심스럽게 정의해보자. 부도체를 정의하려면 전자가 꽉 찬 원자가띠와 텅 빈 전도띠의 개념이 필요하다. 즉 최소한 두 개의 에너지띠가 존재해야 하고, 이는 단위세포^{unit cell}에 적어도 두 개의 오비탈 혹은 두 개의 원자가 존재해야 한다는 뜻이다. 실제로 \(P=1/2\)을 보이는 부도체의 대표적인 예인 Su-Schrieffer-Heeger^SSH 모델[9]은 위에서 정의한 원자핵 대신에 두 개의 원자로 구성된 단위 세포를 도입하여 두 개의 에너지띠 구조를 만들어주었다. 이 경우 전자가 단위 세포 중간에 위치하면 \(P=0\), 이웃한 단위세포 경계에 존재하면 \(P=1/2\)이 된다. 여기서 전자의 의미도 좀 더 조심스럽게 생각해보아야 한다. 앞에서 설명했듯이 주기적인 격자에서 전자는 블로흐 파동 형태로 격자 전체에 퍼져서 존재한다. 원자가띠를 꽉 채우고 있는 전자파동을 잘 중첩하면 실공간에서 국소화 된^localized 파동을 만들 수 있는데, 이렇게 실공간에 국소화 된 원자가띠의 전자 파동을 바니어 함수^{Wannier function}라고 부른다.

위에서 이야기한 전자는 바니어 함수 형태의 국소화 된 전자상태를 말하고, 편의상 바니어 함수의 센터^{Wannier center}를 전자가 존재하는 위치로 정의한다. 1차원 부도체에서는 항상 원자가띠 전자가 국소화 된 바니어 함수를 만들 수 있다. 결국 바니어 센터의 위치가 단위세포 중심에 있는지 경계에 있는지가 \(P=0, P=1/2\)을 결정한다.([그림6-a] 참고) 두 경우 모두 국소화 된 전자와 원자핵의 개념을 써서 기술이 가능하므로 원자 부도체에 해당한다. 하지만 \(P=1/2\)의 경우는 전자가 원자핵에 갇혀 있지 않고 이웃한 두 원자 사이에 존재하는 이상한 상태로, 단순한 원자 부도체와는 구분된다. 이런 형태의 독특한 원자 부도체를 가로막힌 원자 부도체^{obstructive atomic limit}라고 부른다. 가로막힌 원자 부도체는 원자 부도체이긴 하지만 단순한 원자의 집합과는 구분된다. 실제로 \(Mz\) 거울 대칭성이 유지되는 한 단순 원자 부도체와 가로막힌 원자 부도체는 연속적인 변형으로 연결될 수 없고, 반드시 중간에 에너지 갭이 0이 되는 위상상전이 과정을 거쳐야 전이가 가능하다.

이제 가로막힌 원자 부도체의 0차원 가장자리 금속 상태에 대해 이야기를 해보자. 이를 위해서 주기성이 있는 SSH 모델을 생각하고 임의의 이웃한 두 단위세포 사이의 경계를 끊어서 가장자리 두 개를 만드는 과정을 생각해보자. \(P=1/2\) 부도체의 경우 전자 1개가 두 단위세포 경계의 중심에 위치하므로 \(Mx\) 대칭성을 유지하면서 SSH 모델을 끊으면 각 모서리에는 전자가 \(1/2\)씩 나뉘어 들어가야 한다. 이렇게 \(1/2\) 전하가 가장자리에 나타나는 현상을 전하의 분수화^{fractionalization}라고 하는데, 사실 이 문제는 좀 더 조심스럽게 다루어야 한다. 사실 전자 1개의 전하를 더 잘게 쪼갤 수는 없기 때문이다. \(P=0\) 그리고 \(P=1/2\) 1차원 부도체의 가장자리 상태를 엄밀하게 이해하려면 유한한 크기를 가지는 시스템의 에너지 스팩트럼에서 상태수^{state number}를 조심스럽게 따져보아야 한다. 두 시스템의 에너지 스팩트럼은 [그림6-b]를 참고할 수 있다.

유한한 크기를 갖는 시스템이 \(2N\)개의 단위세포로 구성되었다고 하면, 총 \(4N\)개의 상태가 존재하고 이중 \(2N\)개가 전자로 채워져 있어야 한다. \(P=0\) 부도체는 \(2N\)개의 상태가 페르미 준위 아래에, 나머지 \(2N\)개의 상태가 페르미 준위 위에 존재하며, 아래쪽의 \(2N\)개의 상태가 정확하게 전자로 꽉 차게 된다. 반면 \(P=1/2\) 부도체는 \(2N-1\)개의 상태가 페르미 준위 위에, \(2N-1\)개의 상태가 페르미 준위 아래에 존재하고, 에너지가 0인 상태가 두 개 나타난다. 이 두 개의 제로 에너지 상태가 양쪽 가장자리에 국소화 된 상태이다. 여기에 2N개의 전자를 낮은 에너지 준위부터 채우면 우선 \(2N-1\)개의 페르미 준위 아래에 있는 상태들이 꽉 차게 되고, 남은 전자 1개는 두 개의 제로 에너지 상태 중의 하나를 채워야 한다.

문제는 둘 중 어느 하나를 채우게 되면 두 가장자리 중 어느 하나에만 전자가 들어가므로 \(Mx\) 대칭성은 반드시 깨지게 된다. 결국 \(Mx\) 대칭성을 유지하면서 \(2N\)개의 전자를 채울 수 있는 방법이 없다. 이런 현상을 채움 이상^{filling anomaly}이라고 부른다. 채움 이상 현상을 해결하는 한 가지 방법은 \(Mx\) 대칭성을 살짝 깨서 전자가 한쪽 가장자리를 차지하게 하는 것으로, 이렇게 하면 전자가 채워진 가장자리는 평균전하보다 전하가 \(1/2\)만큼 더 쌓여있고, 그 반대쪽은 \(1/2\)만큼 전자가 덜 쌓여있게 만들어서 가장자리 분수 전하를 설명할 수 있게 된다. 하지만 이 방법은 \(Mx\)가 정확하게 유지되어 있지 않아서 시스템의 전기분극이 \(P=0, P=1/2\)로 양자화되는 설명과 배치되는 부자연스러움이 있다.

대칭성을 유지하면서 채움 이상 문제를 이해하는 방법은 시스템에 전자 하나를 추가로 넣거나, 뺀 뒤 전체 전하분포를 확인하는 것이다. 전자를 하나 추가하는 경우를 생각하면 제로에너지 상태 두 개가 모두 전자로 채워지면서 전체 시스템의 전자는 \(2N+1\)개가 된다. 이 경우 추가로 넣어준 전자의 전하분포를 조사하면 양쪽 가장자리에 모두 \(1/2\)만큼의 전하가 추가로 나타나게 된다. 여기서 중요한 것은 \(Mx\) 대칭성을 유지하는 한 \(P=0\)인 부도체는 항상 (\(2N\)+짝수) 만큼의 전자가 채워질 수 있고, \(P=1/2\)인 부도체는 항상 (\(2N\)+홀수) 만큼의 전자가 채워질 수 있어서, 두 부도체는 상태수 개수 비교를 통해서 항상 구분이 가능하다.([그림6-b] 참고) 채움 이상은 일반 원자 부도체와 가로막힌 원자 부도체를 구분하는 가장 일반적인 현상으로 어느 차원의 물질에서도 적용이 가능하다.

이번엔 0차원 꼭지점에 국소화 된 전하를 가지는 2차원 부도체 상태를 생각해보자. 1차원에서와 비슷한 가로막힌 원자 부도체 상태를 얻기 위해서는 추가적인 격자 대칭성이 필요한데, 여기서는 2차원 평면에 수직인 축 방향으로 4중 회전 대칭성^{C4 rotation symmetry}이 있는 전자계를 생각해보자.[10] 스핀-궤도 결합은 무시하고 전자가 스핀이 없는 페르미온^{spinless fermion}이라고 하자. 전체 시스템이 사각 격자^{square lattice} 모양이고, 단위 세포 중심에 4개의 오비탈이 놓여있으며, 단위 세포당 2개의 전자가 있다고 하자. 이 시스템은 4개의 에너지 띠를 가지게 되는데, 이중 2개는 전도띠, 나머지 2개는 원자가띠를 만든다고 하자. 단위세포당 2개씩 들어있는 전자는 원자가띠를 꽉 채우고, 전체 시스템은 부도체 상태가 된다. 4중 회전 대칭성을 만족하면서 2개의 전자가 분포되는 방식은 두 가지가 가능하다. 하나는 단위세포 중심에 있는 오비탈과 같은 위치에 국소화 되는 것이고 다른 하나는 4개의 이웃한 단위세포가 만나는 꼭지점에 2개의 전자가 국소화 되는 것이다.([그림6-c] 참고) 전자는 일반 원자 부도체 상태에 해당하고 후자는 가로막힌 원자 부도체 상태에 해당한다. 4중 회전 대칭성이 유지되는 한 두 부도체 상태들이 연속적인 변형을 통해서 연결될 수는 없다.

이 경우 채움 이상 현상은 어떻게 나타날까? 이를 확인하기 위해서 주기적인 2차원 구조를 가지는 사각 격자를 [그림6-c]처럼 4중 회전 대칭성을 유지하면서 수직, 수평방향으로 잘라서 유한한 크기의 격자로 만들어보자. 4개의 이웃한 단위세포가 교차하는 꼭지점에 있는 2개의 전자는 4개의 꼭지점으로 나뉘게 되고, 이는 곧 각 꼭지점에 \(1/2\)의 분수 전하가 존재함을 의미한다. 하지만 4중 회전 대칭성이 유지되는 한 2개의 전자를 4개의 코너에 동등하게 나눠서 넣는 것은 불가능하다.

4중 회전 대칭성을 유지하면서 채움 이상현상을 확인하는 방법은 다음과 같다. 실제로 유한한 크기의 사각 격자가 \(2N\)개의 단위 세포로 구성이 되어있다고 하면, 전체 시스템에는 \(8N\)개의 상태가 존재한다. 일반 원자 부도체 상태에서는 \(4N\)개의 전자가 페르미 준위 아래에, 나머지 \(4N\)개의 전자가 페르미 준위 위에 나타난다. 가로막힌 원자 부도체에서는 페르미 준위 위와 아래에 각각 \(4N-2\)개의 에너지 준위가 존재하고 제로 에너지에 4개의 에너지 준위가 존재한다. 4개의 제로 에너지 상태에 2개의 전자가 채워져야 한다.

채움 이상 문제를 해결하기 위해 이 시스템에 2개의 전자를 더해주자. 이 경우 4개의 제로 에너지 상태는 전자로 꽉 채워지게 되고, 총 \(4N+2\)개의 전자가 페르미 준위 밑에 나타나게 된다.([그림6-d] 참고). 추가로 들어간 2개의 전자는 시스템의 가장자리의 4개의 꼭지점에 1/2만큼의 추가 전하를 만들며 국소화 되어 존재한다. 결국 4중 회전 대칭성을 만족하는 유한한 크기의 시스템에서 페르미 준위 밑에 \(4N\)개의 준위가 전자로 채워지는지, \(4N+2\)개의 전자가 채워지는지를 기준으로 일반 원자 부도체와 가로막힌 원자 부도체의 구분이 가능하다. 후자는 시스템 가장자리의 꼭지점에 국소화된 0차원 금속 상태 혹은 분수화 된 추가 전하가 모인 상태를 구현한다.

여기서 한 가지 재미있는 꼭지점 전하 분포를 추가로 생각해보자. 사각형 형태로 만든 2차원 물질의 4개의 꼭지점에 플러스, 마이너스 전하가 시계 방향으로 교대로 번갈아 나타나는 부도체 구조를 생각해보자. 이런 전하분포는 전기 단일극 모멘트^{electric monopole moment, 혹은 총전하}와 2중극 모멘트^{dipole moment, 혹은 전기 분극}는 모두 0이지만 유한한 4중극 모멘트^{quadrupole moment}를 가지는 구조이다. 이렇게 덩치상태가 4중극 모멘트를 가지면 1차원 가장자리에서는 전기 분극이 나타나고, 두 전기 분극이 만나는 꼭지점에서는 전하가 쌓이는 현상이 나타나는데, 이는 0차원 꼭지점에 국소화 된 전하가 나타나는 아주 자연스러운 방법이 된다.

이렇게 4중극 모멘트를 가지는 2차원 부도체는 전기 4중극 부도체^{electric quadrupole insulator}라고 부르는데, 이 상태가 사실 0차원 모서리 금속 상태를 가지는 부도체 중 첫 번째로 제안된 예이다.[11] 이런 아이디어가 3차원으로 확장되면 정육면세의 8개의 꼭지점에 양전하와 음전하가 교대로 번갈아 나타나는 부도체 구조를 생각할 수 있고, 이런 상태를 전기 8중극 부도체^{electric octupole insulator}라고 부른다. 전기 8중극 부도체는 덩치상태가 8중극 모멘트를 가지고, 2차원 표면에는 4중극 모멘트, 1차원 모서리에는 전기 분극, 0차원 꼭지점에는 전하를 가지는 특징이 있다.

연약한 위상 부도체^{fragile topological insulator}

위에서 언급한 일반 원자 부도체와 가로막힌 원자 부도체는 페르미 준위 밑 에너지 준위(원자가띠)에 해당하는 전자 파동이 실공간에 국소화 된 바니어 함수로 기술이 될 수 있는 경우에 정의된다. 1차원 격자에서는 주어진 에너지띠에 해당하는 전자 파동의 국소화 된 바니어 함수가 항상 존재하지만, 2차원 이상에서는 그렇지 않다. 사실 양자 홀 부도체와 원자 부도체를 구분하는 또 다른 방법이 바로 각 부도체의 원자가띠에 해당하는 바니어 함수가 존재하는지 여부이다.

천숫자가 유한한 2차원 부도체의 경우 원자가띠 전자는 국소화된 바니어 함수를 만들지 못한다. 비슷하게 2차원 양자 스핀 홀 부도체의 경우도 시간 역전 대칭성을 유지하는 바니어 함수가 존재하지 않는다. 이렇듯 국소화 된 바니어 함수가 존재하지 않는다는 것은 위상숫자를 가지는 위상 부도체라는 말과 동등한 의미가 된다. 위상학적 결정 부도체의 경우, 일반적으로 2차원 표면 금속 상태를 가지는 3차원 1차 부도체, 1차원 모서리 금속 상태를 가지는 3차원 2차 부도체 및 2차원 1차 부도체는 원자가띠에 해당하는 국소화 된 바니어 함수가 존재하지 않는다. 반면 0차원 꼭지점에 국소화 된 전자 상태를 가지는 3차원 3차, 2차원 2차, 1차원 1차 부도체는 국소화 된 바니어 함수가 존재하며, 바니어 센터가 원자에 속박되어 있는지 단위세포 경계에 존재하는지를 기준으로 일반 원자 부도체와 가로막힌 원자 부도체로 구분된다.

그렇다면 0차원 꼭지점에 국소화 된 전자상태를 가지는 위상학적 결정 부도체는 항상 바니어 함수로 기술될 수 있는지를 물을 수 있다. 이 질문의 반례에 해당하는 상태가 바로 연약한 위상 부도체^{fragile topological insulator}다.[12] 연약한 위상 부도체는 2차원 및 3차원에 존재하는데, 모두 물질 가장자리 꼭지점에 국소화 된 전자를 가지지만 해당 원자가띠에 해당하는 파동함수는 양자 홀 상태와 마찬가지로 국소화 된 바니어 함수를 만들지 못한다. 즉 원자 상태를 기반으로 해당 위상 성질을 이해할 수 없다는 뜻이다.

연약한 위상 부도체의 가장 독특한 성질은 원자가띠에 위상 성질이 없는 에너지띠를 추가로 집어넣으면 전체 원자가띠에 해당하는 바니어 함수를 만들 수 있게 된다. 이런 성질은 양자 홀 부도체와 같이 안정된 위상성질^{stable topology}를 가지는 부도체와 구분이 된다. 양자 홀 부도체에서는 원자가띠에 위상성질이 없는 에너지띠를 아무리 많이 추가해도, 전체 원자가띠에 해당하는 바니어 함수가 존재하지 않는다. 이런 안정된 위상성질과 대조를 위해 연약한 위상성질^{fragile topology}라는 개념이 도입되었다. 흥미롭게도 이런 연약한 위상성질을 가지는 에너지띠가 최근에 발견된 마술각 뒤들린 두 층 그래핀^{magic angle twisted bilayer graphene}에서 발견이 되었다. 이 시스템의 페르미 준위 근처에 존재하는 평평한 에너지 띠들이 연약한 위상성질을 가지는 위상학적 상태의 최초의 예로 확인이 된 것이다.[13]  

맺음말: 위상 물질의 완벽한 분류^{complete classification of topological phases}

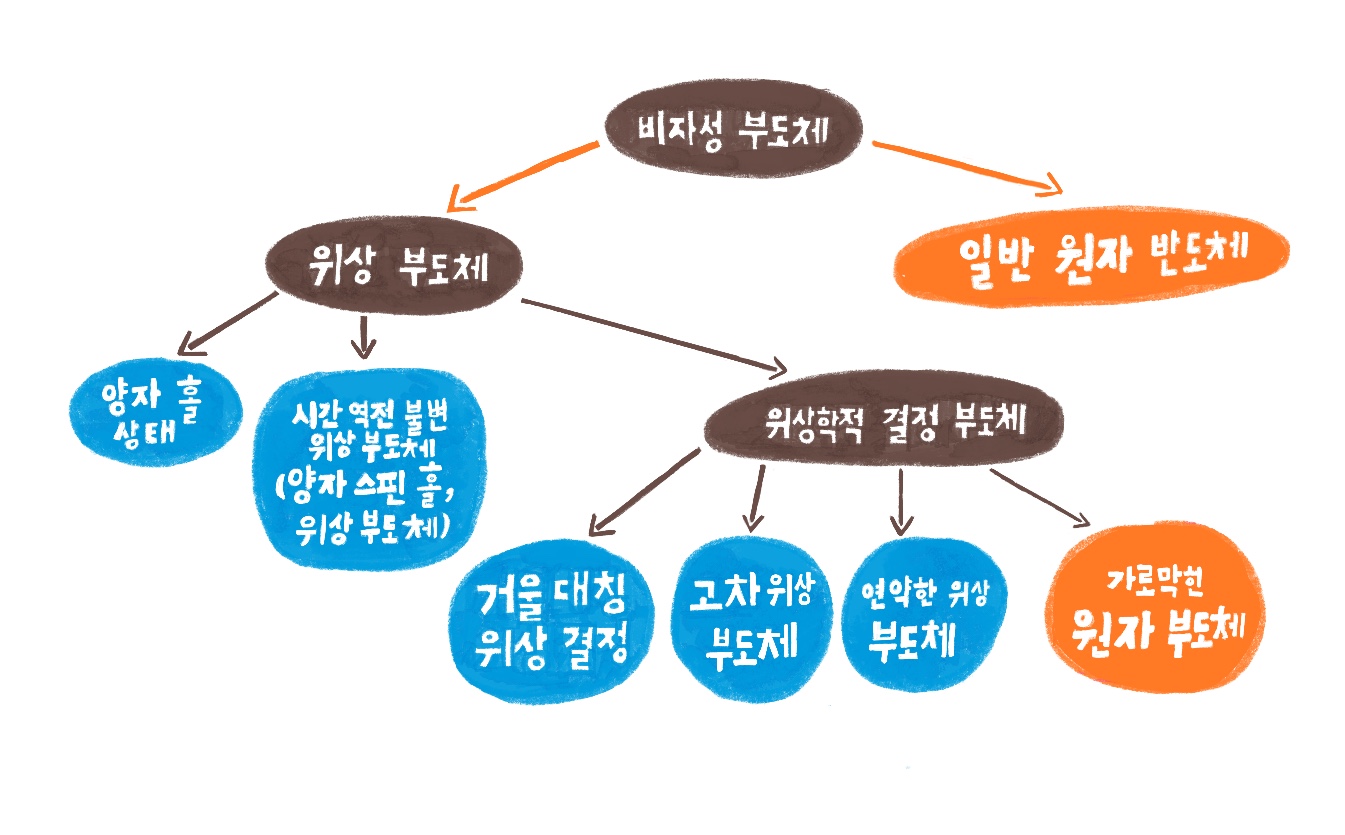
지금까지 최근 15년간 이루어진 위상 부도체 연구의 발전 과정을 간략히 살펴보았다. 2005년 케인 교수와 멜레 교수가 양자 스핀 홀 절연체의 존재 가능성을 이론적으로 예측하기 전까지 부도체를 위상학적으로 분류할 수 있다는 개념은 존재하지 않았다. 당시에 알려졌던 양자 홀 상태는 사실 부도체의 하나라기보다는 자기장 하에서 나타나는 독특한 위상현상으로 부도체 물리와는 별개로 여겨졌다. 양자 스핀 홀 부도체의 발견 이후 대칭성을 기반으로 주기적인 격자 구조를 가지는 시스템의 에너지띠 구조의 위상학적 특성을 분류할 수 있음이 알려졌고, 격자의 결정 대칭성으로 대칭성의 범위가 확장되면서 다양한 형태의 위상학적 결정 부도체가 발견되었다. 본 글에서 살펴본 부도체의 종류는 [그림7]처럼 간략하게 정리할 수 있다.

꽤 여러 가지 종류의 부도체 상태에 대해 이야기를 했지만, 사실 이 글에서 다룬 위상 부도체의 종류는 고체 결정에서 존재 가능한 위상 상태의 일부분에 불과하다. 글을 마무리하기 전에 본 글에서 다루지 않은 위상상태들에 대해서 간략히 언급하고자 한다. 본 글에서 다루지 않은 위상상태 중 하나는 위상 준금속^{topological semimetal} 상태이다. 전도띠와 원자가띠가 에너지 갭으로 분리된 부도체와 달리, 위상 준금속 상태에서는 전도띠와 원자가띠가 브릴루앙 영역의 몇 개의 점, 선, 면에서 맞닿고 있다. 이런 준금속 상태를 각각, 위상 마디점^{nodal point}, 마디선^{nodal line}, 마디면^{nodal surface} 준금속이라고 한다. 마디점에서 2중 혹은 4중 축퇴도를 가지는 바일 준금속^{Weyl semimetal}[14] 및 디락 준금속^{Dirac semimetal}[15]이 대표적인 예이다. 시스템이 가지는 대칭성에 따라 나타날 수 있는 마디점, 마디선, 마디면의 종류와 성질, 그리도 이런 마디들이 나타나는 브릴루앙 영역의 위치가 다르다. 위상 부도체와 마찬가지로 많은 마디선 준금속들이 표면 금속 상태를 가질 수 있고, 여러 가지 다양한 형태의 전자기적 성질을 가지고 있는데, 현재 이에 대한 연구가 활발히 이루어지고 있다.

또한 본 글에서 다룬 위상 부도체는 자성이 없는 물질에 국한하였다. 만약 스핀의 정렬까지 고려하면, 3차원 고체 결정의 공간군 대칭성의 종류는 230개에서 1651개로 늘어난다. 이렇게 다양한 형태의 자성 공간군 대칭성^{magnetic space group symmetry}의 종류는 스핀 정렬을 고려했을 때 나타날 수 있는 위상 부도체, 위상 준금속 상태의 종류 역시 더 다양함을 의미한다.

위상학적 밴드구조에 대한 아이디어는 또한 초전도체^{superconductor}로도 확장이 가능하다. 초전도체와 부도체는 완전히 다른 성질을 가지는 물질 상태이지만 준입자^{quasi-particle}의 에너지 스팩트럼만 고려하면 비슷한 특징을 가진다. 초전도체의 준입자 에너지 스팩트럼은 격자 대칭성과 더불어 입자-반입자 대칭성^{particle-hole symmetry}를 가지는데, 이런 대칭성은 부도체에는 존재하지 않는 대칭성으로, 초전도체는 부도체에는 없는 새로운 위상학적 상태를 구현할 수 있다. 특히 위상 초전도체^{topological superconductor}의 표면에는 마요라나 상태^{Majorana state}라는 표면상태가 존재하는데, 이런 입자는 향후 양자컴퓨터 개발에 응용될 가능성이 높아 최근 많은 주목을 받고 있다.

부도체, 준금속, 초전도체에 자성 공간군 대칭성까지 고려하면, 얼마나 많은 위상 상태를 만들 수 있을까? 고체 격자가 가지는 수많은 대칭성을 고려하면, 가능한 위상 상태를 체계적으로 분류하고 그 성질을 조사하는 것이 근본적으로 가능하기는 한지 하는 의문마저 든다. 많은 위상물질 연구자들이 이런 야심 찬 목표를 이루기 위해 분주히 움직이고 있다. 이미 대칭성 지표^{symmetry indicator}[16] 및 위상학적 양자 화학 ^{topological quantum chemistry}[17] 등의 아이디어를 기반으로 이 복잡한 물질군들을 체계적으로 이해하려는 노력들이 조금씩 결실을 맺고 있다.

위상 물질 연구가 짧은 시간 동안 큰 발전을 이룩한 것은 사실이지만, 동시에 많은 새로운 문제들, 그리고 질문들을 만들어냈다. 모든 물질을 대칭성과 위상 성질을 기반으로 분류하는 일, 각 위상상태의 독특한 물성을 밝히는 일, 상호작용 효과를 이해하는 일, 그리고 서로 다른 위상 상태 사이의 양자 상전이^{quantum phase transition} 현상을 이해하는 일 등 후학들이 해결해야 할 문제들이 산더미처럼 쌓여 있다.