2018년 봄, 로스앤젤레스
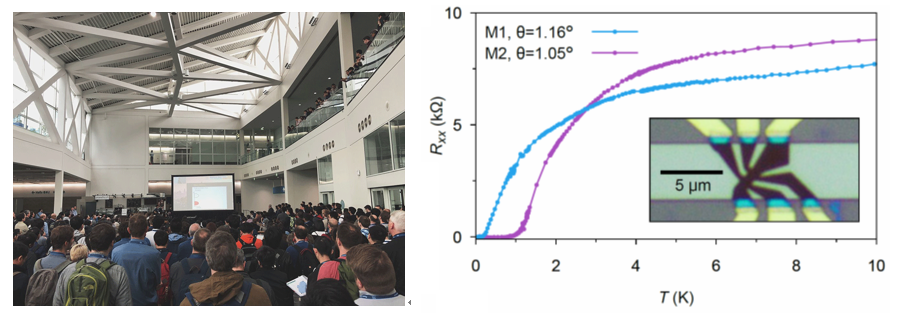
2018년 3월 첫째 일요일, 여느 해와 마찬가지로 인천공항에서 미국행 비행기에 몸을 실었다. 응집물질물리 분야에서 세계 최대 학술행사인 3월 미팅March Meeting에 참석하는 길이었다. 새 학기가 막 개강한 직후라서 강의를 1주일 미루고 출장을 떠나기가 매년 그렇듯이 상당히 부담스러웠다. 하지만, 매년 연구를 진행하기 위해서는 어쩔 수 없는 일정이었다. 미국 물리학회의 3월 미팅은 항상 지나간 1년의 연구 방향을 돌아보고 새로운 연구 방향을 가늠하는 중요한 기점이었다. 2018년 3월 미팅은 한인 교포들이 많이 사는, 기후도 온화한 미국 로스앤젤레스Los Angeles에서 개최되었다.
3월 미팅에서는 응집물질물리학 분야 연구자들이 심혈을 기울인 엄청난 수의 연구 성과들이 군더더기 없이 간결하게 발표된다. 2018년 3월 미팅에서는 1만여 편의 발표가 예정되어 있었다. 한 발표자에게 기본 시간으로 12분씩 주며, 수십 개의 발표장에서 오전 8시에 시작하여 오후 5시 30분까지 연구 발표가 진행된다. 점심 시간도 없이 하루 중 오전에 15분, 오후에 15분, 이렇게 휴식 시간을 딱 2번만 주면서, 집중도를 최대로 끌어올린다. 한국에서 출발하여 개최 도시에 도착하면 시차로 밤낮이 뒤집어진 상태에서 체력 부담도 상당하지만, 3월 미팅에서 관심있는 연구 주제를 찾아 연구 발표를 계속 들으며 지난 1년의 연구 성과를 정리하고 앞으로의 연구 방향을 깊이 생각할 수 있다. 그리고 몇 년에 한 번씩은 아주 놀라운 연구 결과가 발표되어 새로운 연구 주제가 열린다.
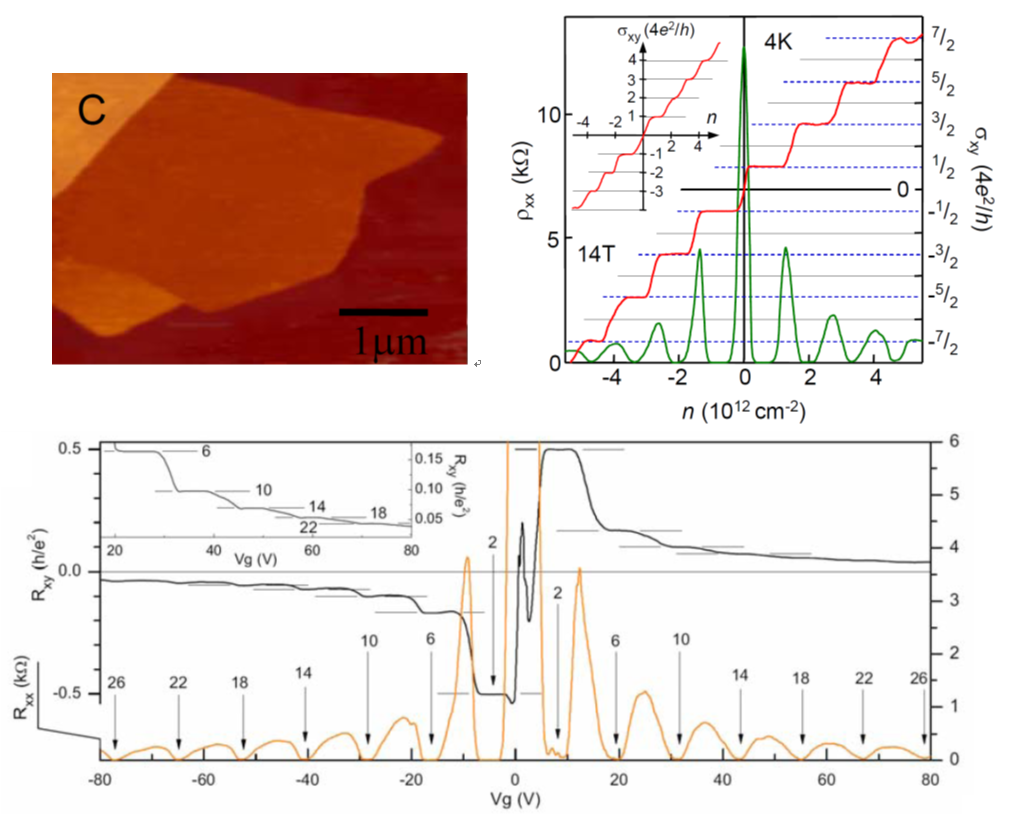
2018년 3월 미팅에서 1일 차인 월요일과 2일 차인 화요일이 지나가고 3일 차인 수요일이 되었을 때 학회장인 로스앤젤레스 컨벤션 센터의 분위기가 술렁이고 있었다. 매사추세츠 공대Massachusetts Institute of Technology, MIT의 파블로 하리요-에레로Pablo Jarillo-Herrero 교수의 발표를 컨벤션 센터의 열린 공간에서 생중계로 중계 방송한다는 것이었다. 하리요-에레로 교수가 어느 발표장에서 발표할 예정인데, 그 발표장에 들어갈 수 있는 인원보다 훨씬 많은 사람들이 하리요-에레로 교수의 발표를 듣고자 할 것으로 예상되어 그 발표장에 중계 카메라를 설치하고 열린 공간에 대형 TV를 놓아 생중계한다는 것이었다. 20년 동안 3월 미팅에 참석하였지만 연구 발표를 생중계하는 경우는 거의 없었던 듯하다. 중요한 발표임을 직감하고 대형 TV에 되도록 가까운 위치에서 발표를 들었다.
하리요-에레로 교수가 발표한 연구 결과는 역시 아주 놀라웠다. 그래핀 위에 다른 그래핀을 놓을 때 두 그래핀의 방향을 1도 정도 다르게 하면 전기가 통하지 않는 부도체가 되게 하거나 전기 저항이 전혀 없는 초전도체가 되게 할 수 있다는 내용이었다.[1,2] 탄소로 이루어진 그래핀 한 장은 전기가 잘 통하는 도체이지만 전기 저항이 아주 없는 물질은 아니다. 중고등학교 때 배운 과학 실력으로 생각하면 그래핀 두 장을 겹치면 전기가 2배로 잘 흘러야 한다. 즉 1+1=2이다. 그런데 하리요-에레로 교수의 발표 내용은 그래핀 두 장을 겹쳐서 전기가 전혀 흐르지 않게 하거나(즉 1+1=0), 또는 전기가 무한대로 잘 흐르게(즉 1+1=무한대) 할 수 있다는 내용인 것이다. 하리요-에레로 교수의 발표가 끝난 후, 근처에서 발표를 들은 최영우 학생이 상기된 표정으로 필자에게 다가왔다. “교수님, 계산해 볼까요?”
탄소: 그래핀의 구성 원소
그래핀은 탄소 원자가 한 층으로 배열되어 이루어진 물질이다. 탄소는 우리의 일상과 아주 밀접하다. 우리 몸을 구성하는 중요한 원소 중의 하나이고, 식물이 광합성으로 태양 에너지를 저장하여 우리에게 전달하는 과정에서도 아주 중요한 성분이다. 음식을 먹으면 탄소가 우리 몸속에 들어와 산소와 결합하면서 생명에 필요한 에너지를 공급한다. 인간이 아주 오랜 옛날에 불을 피워 문명의 길을 시작할 때 불꽃 속에서 산소와 결합하면서 빛과 열을 낸 것도 탄소이다. 옛날 생물들의 유해인 석유와 석탄의 주된 성분이며 우리가 입는 옷과 사용하는 플라스틱 등의 주된 성분이기도 하여, 주위에서 탄소가 들어 있지 않은 것을 찾는 것이 오히려 퀴즈가 될 듯하다. 이렇게 중요한 탄소이지만 아이러니하게도 산소와 결합하여 생기는 이산화탄소는 지구 온난화의 주범으로 지목되어 퇴출 대상이기도 하다.
탄소는 수없이 많은 종류의 물질에서 다양한 역할을 해내고 있다. 탄소가 이럴 수 있는 것은 탄소 원자가 가장 바깥쪽의 전자 껍질에 전자 4개를 가지고 있고 그 안쪽의 전자 껍질에는 s 궤도 함수orbital만 있기 때문이다. 원자의 가장 바깥쪽 전자 껍질에 있는 전자를 최외각 전자라 부르며, 이 전자들은 화학 결합과 전기적 성질에 중요한 역할을 담당한다. 탄소는 최외각 전자 4개를 가지고 주위의 다른 원자 1개 또는 2개 또는 3개 또는 4개와 화학 결합을 할 수 있어서 무수히 많은 구조의 분자와 고체를 만들 수 있다.
다이아몬드와 흑연, 그리고 그래핀
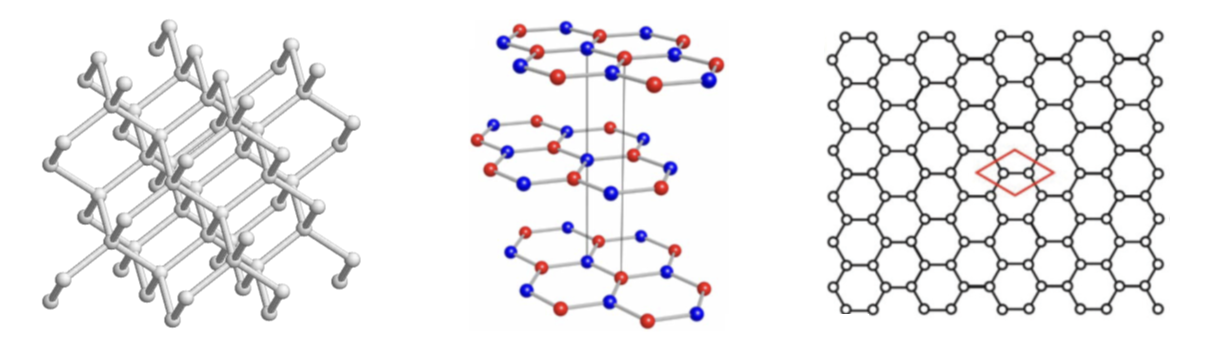
탄소로 만들어진 고체로서 대표적인 것이 다이아몬드와 흑연이다. 다이아몬드는 투명하고 단단하고 귀하다. 다이아몬드에서는 탄소 원자들이 각각 그 주위에 있는 다른 탄소 원자 4개와 공유 결합을 단단히 하고 있는데, 이 공유 결합에 최외각 전자 4개를 모두 사용하여, 자유롭게 이동할 수 있는 자유 전자가 없다. 이리하여 다이아몬드는 단단하고 전기가 흐르지 않는 부도체이다.
이와 달리 흑연은 검고 잘 부서지고 흔하다. 연필심에 들어 있는 것이 다 흑연이다. 흑연은 평면 모양의 탄소 층들이 쌓여 있는 구조이다. 같은 층 안의 탄소 원자들이 강하게 결합하여 탄소 층 각각은 강하지만, 탄소 층 사이의 결합은 약하여 탄소 층들이 서로 쉽게 떨어질 수 있다. 우리가 연필을 종이에 문지르면 연필심이 닳으면서 종이에 검은색이 묻는데 이 검은색이 흑연에서 떨어진 탄소 층들이다. 흑연에서 탄소 원자들은 최외각 전자 4개 중 3개를 사용하여 같은 층에 있는 다른 탄소 원자 3개와 공유 결합을 단단히 하고, 남은 전자 1개는 자유롭게 이동할 수 있는 자유 전자가 된다. 이 자유 전자로 인하여 흑연은 전기가 잘 흐르는 도체이다.
그래핀은 흑연의 탄소 층 하나가 따로 분리되어 있는 경우이다. 그래핀은 단단하면서도 휘어지고, 전기가 잘 통한다. 그래핀의 존재는 20세기 후반에 이미 알려져 있었으나, 그래핀을 쉽게 만들 수 있는 방법은 비교적 최근인 2004년에 전 세계 연구자들에게 알려졌다.[5]
나노미터의 세계
그래핀의 두께는 1나노미터(nm)보다 작다. 1나노미터는 10억분의 1미터(m)이다. 그래핀처럼 원자 한 층으로 이루어진 물질은 엄밀히 말하면 두께가 없다고 할 수도 있지만, 그래핀을 여러 층 쌓으면 그래핀 사이의 간격이 0.33 나노미터가 되므로, 그래핀의 두께는 실질적으로 0.33 나노미터라 할 수 있다. 즉, 그래핀의 두께는 30억분의 1 미터이다. 그래핀은 종이보다 얼마나 얇은 것일까? 프린터에 사용하는 종이 500매 한 묶음을 꺼내어 두께를 자로 재 보았다. 약 5센티미터(cm)이었다. 그러면 종이 한 장의 두께는 즉 1만분의 1 미터이다. 1만의 30만 배가 30억이므로 그래핀은 종이보다 30만분의 1배 얇은 것이다. 여러분의 키가 30만분의 1배로 줄어들면 그래핀이 종이처럼 보일 것이다.
이렇게 작은 세계는 1981년 IBM 취리히 연구소의 게르트 비니히Gerd Binnig 박사와 하인리히 로러Heinrich Rohrer 박사가 주사 터널링 현미경Scanning Tunneling Microscope, STM을 발명하면서 물질적으로 다룰 수 있게 되었다.[6] 주사 터널링 현미경은 아주 뾰족한 금속 바늘을 1 나노미터보다 작은 크기로 움직이면서 바늘 끝을 이용하여 물질의 모양을 측정하거나 물질을 움직일 수 있는 기술이다. 주사 터널링 현미경은 나노 미터 영역의 과학 기술에 엄청난 발전을 불러왔고, 비니히 박사와 로러 박사는 전자 현미경을 설계한 에른스트 루스카Ernst Ruska 박사와 함께 불과 5년 뒤인 1986년에 노벨 물리학상을 수상하였다. 주사 터널링 현미경의 발명이 나노 과학의 세계를 열었다고 할 수 있다.
풀러렌: 나노미터 크기 탄소 축구공
그래핀과 같은 탄소 나노 물질의 선두 주자는 축구공 모양의 풀러렌fullerene이다.[9] 풀러렌은 1985년에 미국 라이스Rice 대학의 로버트 컬Robert F. Curl 교수, 영국 서식스Sussex 대학의 해롤드 크로토Harold W. Kroto 교수, 미국 라이스 대학의 리차드 스몰리Richard E. Smalley 교수의 연구팀이 우주에 있을 수 있는 탄소 물질을 찾던 중에 우연히 합성되었다.[9]
크로토 교수는 그 당시에 우주 공간에 어떤 탄소 물질이 있는지 관심이 많았고, 탄소로 이루어진 기다란 분자가 우주 공간에 있을 것으로 예상하였다. 우주 공간에 어떤 물질이 있는지 어떻게 알아낼 수 있을까? 방법은 우주에서 오는 빛, 적외선, 마이크로파 등 여러 전자기파들을 분석하는 것이다. 우주에서 오는 전자기파들이 우주 공간에 있는 물질을 지날 때, 물질에 따라 특정한 진동수의 전자기파는 물질에 흡수되어 지구에 도달하지 못하고, 다른 진동수의 전자기파는 물질을 그대로 통과하여 지구에 도달한다. 우주에서 오는 전자기파들을 분석하여, 없어진 진동수를 찾고, 어떤 물질이 그런 전자기파를 흡수하는지 알아내면 그 물질이 우주 공간에 있다는 것을 알 수 있다. 한편으로는 우주에서 분자가 생성되는 상황을 실험실에서 흉내 내어 물질을 합성하고, 그 물질이 어떤 진동수의 전자기파를 흡수하는지 실험하여 우주에서 오는 전자기파와 비교하면 그 물질이 우주 공간에 있는지 없는지 알 수 있다.
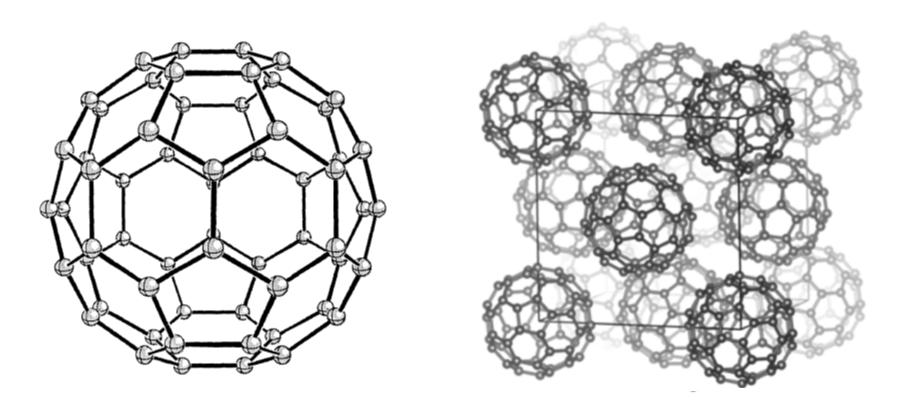
크로토 교수는 스몰리 교수 연구팀에 특별한 합성 장치가 있는 것을 알게 되었고, 1985년 9월 1일에 라이스 대학 스몰리 교수 연구실에 도착하여 공동 연구를 시작하였는데, 컬 교수도 연구에 참여하였다. 이들은 흑연의 표면에 레이저를 비추어 탄소 기체를 만든 후, 이 탄소 기체가 응축할 때 어떤 탄소 분자가 생기는지 실험하였다. 합성된 탄소 분자들의 질량을 분석한 결과, 뜻밖에도 탄소 60개 또는 탄소 70개로 이루어진 탄소 분자가 잘 생기는 것을 발견하였고, 탄소 원자들이 각각 그 주위의 다른 탄소 원자 3개와 결합하여 둥근 풍선과 같게 된 것이라 예상하였다.
이들은 이와 비슷한 모양의 건축물을 설계했던 건축가 버크민스터 풀러Buckminster Fuller의 이름을 따서 합성된 탄소 분자의 이름을 풀러렌fullerene이라 하였고, 1985년 9월 12일에 논문 작성을 마무리하였다. 특히, 탄소 60개로 이루어진 분자는 축구공과 같이 5각형 12개와 6각형 20개로 이루어진 다면체 모양의 꼭지점에 탄소 원자들이 놓인 구조일 것이라 예상하고 논문에 축구공 사진을 넣었다.[9] 탄소 원자로 이루어진 풍선 모양의 구조가 과학계에 처음 보고된 것이었으며 컬, 크로토, 스몰리 교수는 풀러렌을 발견한 공로로 1996년에 노벨화학상을 받았다.
풀러렌 고체
풀러렌 연구 초기에는 합성된 풀러렌의 양이 적어서 주로 분자 상태의 연구가 진행되었는데, 풀러렌을 합성하는 방법이 발전되면서 풀러렌을 많이 만들 수 있게 되었고 풀러렌으로 고체를 만들어 연구할 수도 있게 되었다.[10] 풀러렌이 모여 만들어지는 고체는 면심입방구조faced centered cubic를 가지고 있으며[10], 풀러렌 고체에 알칼리 금속을 첨가하면, 알칼리 금속에서 전자가 떨어져 나와 풀러렌 고체 속을 흐르는 도체가 된다.[11] 첨가되는 알칼리 금속의 양이 풀러렌 분자 1개 당 알칼리 금속 원자 3개의 비율이 되면 낮은 온도에서 풀러렌 고체의 전기 저항이 완전히 사라지는 초전도체가 되고[12], 첨가되는 알칼리 금속의 종류를 바꾸면 초전도성이 발생하는 최대 온도가 달라진다.[13]
필자가 풀러렌을 처음 본 것은 1990년대 초이다. 서울대의 박영우 교수님 실험실에서 대학원 선배들이 풀러렌으로 실험하는 것을 옆에서 볼 수 있었다. 이때는 필자가 실험실의 신참내기로 여러 실험을 보고 배우던 때이다. 선배가 압력을 가할 수 있는 작은 통에 풀러렌 분말을 아주 조심하여 넣고 압력을 세게 가하였다. 압력을 받은 풀러렌 분말은 고체 덩어리가 되었는데 이 고체를 펠렛pellet이라고 불렀다. 그 다음 과정은 못 본 듯한데, 문헌을 찾아보니 풀러렌 펠렛에 알칼리 금속을 첨가하고 온도를 아주 낮은 온도부터 상온까지 변화시키면서 전기전도도와 열전력thermopower 특성을 측정하여 보고한 논문을 찾을 수 있었다.[14]
풀러렌 박막
필자가 풀러렌을 본격적으로 연구한 것은 미국 캘리포니아California 대학 버클리Berkeley 캠퍼스에서 박사후 연구원으로 있었던 2000년대 초이다. 필자는 당시 핫이슈 중 하나였던, 홀 도핑된hole doped 풀러렌 박막의 초전도 특성을 연구하였다. 1990년대에는 전자 도핑된 풀러렌 고체의 초전도 특성이 큰 관심을 받았었는데, 2000년 11월에 미국 벨Bell 연구소의 얀 헨드릭 쇤Jan Hendrik Schön 박사가 전자 대신에 홀을 도핑하여 풀러렌 박막의 초전도 특성을 더 강하게 만들었다는 놀라운 실험 결과를 발표하였다.[15]
필자는 2001년 거의 1년 동안 붕화 마그네슘MgB2의 초전도 특성 계산에 몰입되어 있었는데[16], 다음 연구 주제로 홀 도핑된 풀러렌 박막의 초전도성을 선택하였다. 쇤 박사의 실험 논문을 보면, 전자 도핑된 풀러렌 고체보다 홀 도핑된 풀러렌 박막에서 초전도 특성이 더 강하므로, 필자는 전자 도핑의 경우와 홀 도핑의 경우를 비교하는 방향으로 연구를 진행하였다. 필자가 3개월의 시간을 들여 집중 계산한 결과, 실험 결과와 반대로 전자 도핑된 풀러렌보다 홀 도핑된 풀러렌에서 초전도 특성이 더 약하다는 결론에 도달하였다. 즉, 쇤 박사의 실험 결과는 표준적인 초전도 이론으로 설명할 수 있는 것이 아니었다. 필자는 이에 대해 논문을 쓰지 않고 이 주제에 대한 연구를 종료하였는데, 이후 1년이 채 되기 전에 쇤 박사의 실험 결과들이 사실이 아닌 조작된 것일 수 있다는 이야기가 돌았다. 이에 대해 벨 연구소에서 공식으로 조사한 결과, 사실이 아닌 것으로 판명되었다.[17]
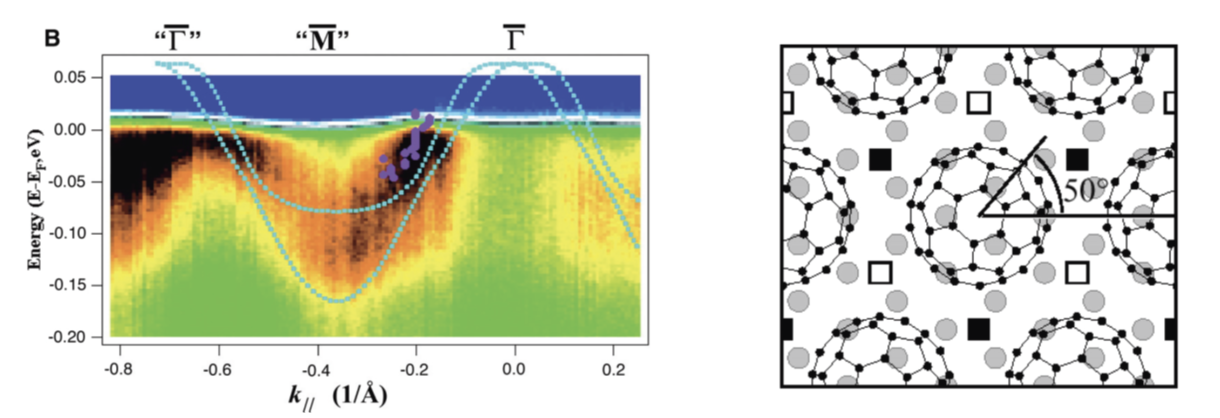
홀 도핑된 풀러렌의 초전도 특성에 대해서는 논문을 쓰지 않고 연구를 종료하였지만, 이때 탄소 원자로 이루어진 다양한 나노 구조에 대해 효율적으로 계산할 수 있는 역량을 갈고 닦을 수 있었다. 이 역량은 곧이어 스탠포드Stanford 대학의 쉔Z. X. Shen 교수 연구팀과 풀러렌 박막의 전자 구조에 대해 공동 연구를 할 때 큰 도움이 되었다. 쉔 교수 연구팀은 은111 표면 위에 풀러렌C60 단일층을 만들고 칼륨을 도핑한 후에 각분해 광전자 방출 분광angle-resolved photoemission spectroscopy, ARPES을 이용하여 칼륨 도핑된 풀러렌C60 단일층에 있는 전자의 에너지-운동량 관계를 측정하였다. 칼륨에서 빠져나온 전자는 풀러렌 단일층이 가지는 전도 띠conduction band의 아래쪽을 채우게 되는데, 칼륨에서 온 전자로 채워진 전도 띠의 에너지 부분이 약 100 밀리 전자 볼트meV로 측정되었고, 필자의 계산으로는 약 170 밀리 전자 볼트이었다.[18] 측정값과 계산값의 차이는 전자와 원자 진동의 상호작용에 의한 것으로 해석되었다.
탄소 나노튜브: 나노미터 굵기 탄소 빨대
1990년대 초 풀러렌을 연구하던 사람들 사이에 소문이 하나 돌았는데, 바로 풀러렌을 합성하는 방법과 비슷한 방법으로 탄소 대롱도 만들어졌다는 것이었다. 소문은 곧 확인되었는데, 1991년 일본의 이지마Iijima 박사가 아크 방전arc discharge 방법으로 탄소 나노튜브를 합성하고 전자현미경 사진을 찍어 학계에 보고하였다.[19] 탄소 나노튜브는 [그림5]와 같이 탄소 원자로 이루어진 빨대 모양의 고분자 물질이다. 탄소 나노튜브의 지름은 1나노미터 정도로 작을 수 있고 길이는 1 마이크로미터μm 정도로 길 수 있다. 1 마이크로미터는 1백만분의 1미터이다.
수학에서 점은 0차원, 선은 1차원, 면은 2차원, 공간은 3차원이다. 이를 따르면 풀러렌은 0차원, 탄소 나노튜브는 1차원, 그래핀은 2차원, 흑연과 다이아몬드는 3차원이다. 탄소 나노튜브를 그래핀과 비교하면, 탄소 나노튜브는 그래핀이 둥글게 말려 원통 모양이 된 것과 같다. 탄소 나노튜브에서 전자들이 원통 둘레 방향으로 운동하면 처음 위치로 돌아오므로 전자의 양자역학적 파동 함수가 원통 둘레 방향으로는 정상파를 이루어 운동량이 양자화된다. 한편, 탄소 나노튜브의 축 방향으로는 운동량이 양자화되지 않아 운동량이 연속적으로 변한다. 탄소 나노튜브는 여러 가지 구조가 가능한데, 원통면에서 탄소 원자들이 만드는 육각형의 꼭짓점 방향이 나노튜브의 축방향과 이루는 각도에 따라 도체가 되기도 하고 반도체가 되기도 한다.[20,22,23]
1990년대 중후반, 탄소 나노튜브를 사용하여 전기 회로를 만드는 실험은 나노 회로 기술을 발전시키는 중요한 계기가 되었다. 앞에서 이야기한 것과 같이 탄소 나노튜브의 지름은 1 나노미터 정도로 작고 길이는 1 마이크로미터 정도로 커서, 아주 작은 도체 도선 또는 반도체 도선과 같다. 1990년대 중반은 나노 회로 기술이 태동하는 상황이어서 탄소 나노튜브 1개에 금속 도선을 연결하여 저항값을 측정할 수 있으면 그 결과를 세계적인 학술지에 논문으로 발표할 수 있었다.[24] 탄소 나노튜브는 학계와 산업계에 지금도 큰 영향을 주고 있으며, 최초로 발견한 이지마 박사가 노벨상 후보로 여러 차례 거론되었으나, 2010년에 그래핀 실험에 노벨상이 수여되면서 탄소 나노튜브에 대해 노벨상이 주춤하고 있는 모양새이다.
탄소 나노튜브의 전기 전도도 계산
필자는 박영우 교수님 연구실에서 고체 실험으로 석사 과정을 마친 후에 박사 과정을 고체 이론으로 하여 임지순 교수님 연구실에 들어갔고 박사 과정 학생이었던 1990년대 중후반에 탄소 나노튜브를 집중적으로 연구하였다. 탄소 나노튜브가 모여 다발이 되는 경우에 전자의 상태가 어떻게 달라지는지 연구하였고[21], 나노 물질의 전기전도 특성에 대한 양자역학적 계산법을 세계에서 처음으로 개발하여 탄소 나노튜브의 전기전도 특성을 정밀하게 연구하였다.[25] 나노 물질의 전기전도 특성 계산법을 개발하는 과정은 두 단계로 이루어졌다. 첫번째 단계는 3차원 나노 구조에서 전자 흐름을 계산할 수 있는 방법론을 개발한 것이었고[26], 두번째 단계는 이 방법론을 탄소 등 나노 구조의 성분 원소를 정확히 고려할 수 있도록 발전시킨 것이었다.[27]
3차원 나노 구조 속에서 전자는 파동적 성질이 강하게 발현되어 파동이 퍼지는 것처럼 나노 구조 속에서 이동한다. 이것은 전자기파가 금속 관 속을 이동할 때와 매우 유사하다. 필자는 학부 양자역학 시간에 배웠던 1차원 장벽 문제를 3차원으로 확장한 방정식을 유도하였고, 이 방정식을 푸는 프로그램을 작성하였다. 이 프로그램에서는 자연계의 인과율에 맞는 순서로 미지수의 값들이 정해지도록 하여 계산결과가 안정적으로 산출될 수 있게 하였다.[26]
이렇게 개발된 방법은 3차원 나노 구조에서 전자의 위치 에너지가 주어졌을 때 전자의 흐름을 계산하는 방법이었지만, 3차원 나노 구조를 원자 수준에서 고려할 수 있는 것은 아니었다. 이러한 수준이 되려면 넘어야 하는 고비가 남아 있었다. 물질의 구조를 원자 수준에서 고려하려면 개별 원자를 나타내는 유사 포텐셜pseudopotential이 비국소적nonlocal 함수라는 것을 고려할 수 있어야 했다. 3차원 나노 구조에서 전자의 흐름을 연구할 때는 전자의 위치 에너지가 국소적local 함수라고 생각하여 국소적 슈뢰딩거 방정식의 해를 구한 것인데, 비국소적 슈뢰딩거 방정식의 해를 구할 수 있도록 방법론을 확장하여야 하는 것이었다. 이에 대해 처음에는 필요한 계산 요소들이 서로 곱셈의 관계가 되어 결과적으로 계산량이 너무 많아서 불가능할 것이라고 생각하였으나 얼마 후 필요한 계산 요소들이 덧셈의 관계가 되어 계산량이 가능한 크기라는 것을 깨닫게 되었다.[27]
나노 물질의 전기전도 특성을 양자역학적으로 계산할 수 있는 프로그램은 당시에 세계의 많은 이론 연구자들이 손에 넣길 원했던 최첨단 연구 기술이었다. 이를 직접 개발함으로써 이후 한동안 탄소 나노튜브의 전기전도 특성 연구에서 가장 앞서 갈 수 있었다. 프로그램의 알고리즘을 자세히 설명한 논문을 발표하였고, 다른 연구자들이 멀지 않아 비슷한 프로그램을 개발할 수 있었는데 이들은 개발 성공을 보이기 위해 필자의 연구 결과를 재현하여 발표하였다.
그래핀: 탄소 원자 층의 재발견
그래핀 이야기로 다시 돌아가자. 2004년 영국 맨체스터Manchester 대학의 안드레 가임Andre Geim 교수와 콘스탄틴 노보셀로프Konstantin Novoselov 박사가 스카치 테이프를 이용하여 흑연으로부터 그래핀을 제작하였다고 학계에 보고하였다.[5] 노보셀로브 박사는 가임 교수의 지도를 받아 2004년에 박사 학위를 받았는데, 스카치 테이프를 이용하여 그래핀을 제작한 것은 박사 학위를 받기 전이었을 것으로 추측된다. 흑연에서 탄소 한 층을 떼어내는 실험이었고, 기계적 박리에 의한 그래핀 제작이라 표현하였다.
흑연과 스카치 테이프를 구하여, 스카치 테이프를 흑연에 붙인 후에 떼면 스카치 테이프에 검은색 흑연 부스러기에 남게 되는데, 붙였다가 떼는 것을 반복하면 아주 미세한 검은색이 스카치 테이프에 붙게 된다. 스카치 테이프를 이산화규소 기판 위에 문지르면 스카치 테이프에 붙었던 검은색 먼지들이 기판에 옮겨 붙는데, 그 검은색 먼지들이 그래핀이다. 아주 저예산의 실험이다. 준비물은 이산화규소 기판, 흑연, 그리고 스카치 테이프이다.
흑연과 스카치 테이프를 이용하여 그래핀을 매우 값싸게 만들 수 있게 되면서 세계적인 연구 열풍이 불었다. 그래핀은 자유 전자들이 상대론적 특성을 가지고 있고, 화학적으로 안정하여 다양한 특성이 예측되었고 실험되었다. 특히, 한국인 과학자들이 그래핀 연구에 크게 기여하여 김필립 교수뿐만 아니라 홍병희 교수, 안종현 교수, 손영우 교수가 세계적으로 큰 파급력 있는 연구 결과들을 발표하였다. 가임 교수와 노보셀로프 박사는 2010년에 그래핀에 대해 중요한 실험을 한 공로로 노벨 물리학상을 수상하였다. 한편, 그래핀과 같은 탄소 원자 층이 가임 교수와 노보셀로프 박사에 의해 최초로 실험된 것은 아니어서, 노벨 물리학상이 수여된 후, 노벨상 수여 이유서에 표현된 그래핀 연구의 역사가 너무 협소하다는 의견이 제기되었다.[30]
그래핀으로 유명한 하버드Harvard 대학 김필립 교수는 박사 과정 학생일 때 탄소 나노튜브 연구를 하였고 1999년 박사 학위 후에 캘리포니아 대학 버클리 캠퍼스에서 박사 후 연구원을 하였다. 필자가 버클리 캠퍼스에 있었던 기간과 상당히 겹친다. 당시 김필립 박사는 탄소 나노튜브를 주로 연구하면서 흑연에서 탄소 원자층을 떼어내는 연구도 관심이 많았다. 필자는 김필립 박사가 탄소 원자층에 대해 언급하는 것을 보면서 저런 연구도 있구나 생각하였는데, 그래핀 연구의 중요성을 그 때에 깨닫았으면 그래핀 연구를 좀더 일찍 시작했을 것으로 생각된다. 당시에 필자는 붕화 마그네슘MgB2의 초전도성 연구에 푹 빠져 있었다.
한편, 김필립 박사는 2002년에 뉴욕에 있는 컬럼비아Columbia 대학의 교수로 부임하여 흑연에서 탄소 원자층을 떼어내는 연구를 하였는데 나노 연필nanopencil이라 명명된 기술집약적 방법으로 2004년에 원자 3층 두께에 도달하였다. 이때 스카치 테이프를 사용하는 값싼 방법이 학계에 보고되면서 그래핀 연구가 세계적으로 급속히 확산되었다. 연구 방법에는 정도가 없고, 연구의 중요도와 연구의 난이도는 서로 관계가 없을 수 있고, 연구 방법은 쉬울수록 좋다는 것을 다시 한번 되새기는 계기가 되었다. 김필립 교수 연구팀에서는 스카치 테이프를 사용하는 방법을 듣게 된 바로 그 다음날부터 스카치 테이프 방법을 사용하기 시작하였다고 한다. 매우 본받을 점이라고 생각한다.
2004년 기계적 박리에 의한 그래핀 제작이 보고된 후 그 다음해인 2005년에 노보셀로프 박사와 가임 교수의 연구팀, 그리고 김필립 교수의 연구팀에서 각각 그래핀에서 발생하는 특이한 양자 홀 효과Hall effect를 보고하였다.[28,29] 그래핀에 전류를 흘리면서 그래핀 면에 수직한 방향으로 자기장을 가하고 전류와 자기장에 수직한 방향으로 전압을 측정하는 홀 효과 실험이었으며, 실험 결과는 보통의 양자 홀 현상과 차이가 있는, 특이한 양자 홀 현상이었다.
그래핀의 제작 과정은 풀러렌이나 탄소나노튜브와 달리 화학 반응을 이용한 것이 아니라, 흑연을 가져다 놓고 스카치 테이프로 떼는 것이다. 스카치 테이프를 사용한 그래핀 연구가 세계적으로 막 확산되던 시기에 연세대 물리학과의 학부생인 김종환 학생(현재 포스텍 신소재공학과 교수)이 미국 캘리포니아 대학 버클리 캠퍼스에 교환학생을 갔다. 김종환 학생은 버클리 캠퍼스에 있는 동안 물리학과의 팽 왕Feng Wang 교수 연구팀에 참여하였는데, 스카치 테이프로 그래핀을 떼어 실험에 필요한 시료를 제작하는 것을 하였다. 이 후, 김종환 학생이 교환 학생을 마치고 연세대로 돌아온 후에 물리학과 대학원생들에게 그래핀의 시료를 제작하는 노우-하우know-how를 전해주었고, 연세대 물리학과 연구실들의 그래핀 및 2차원 물질 연구를 촉진하였다.
그래핀의 원자 구조와 전자 구조
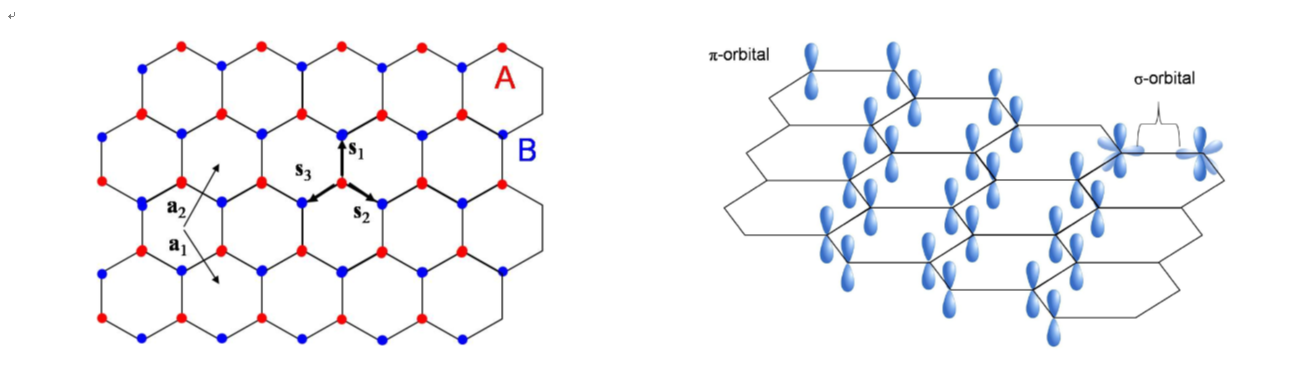
그래핀은 탄소 원자층 하나로 되어 있는데 각각의 탄소 원자가 이웃한 3개의 탄소 원자와 공유 결합을 한다. 이웃한 탄소 원자들을 선분으로 이으면 [그림8]과 같이 육각형이 반복되는 벌집honeycomb 모양이다. 이웃한 탄소 원자 사이의 거리는 약 0.14 나노미터이다. 탄소 원자 하나를 빨간색으로 표시한 후, 빨간색으로 표시된 탄소 원자에 이웃한 탄소 원자를 파란색으로, 파란색으로 표시된 탄소 원자에 이웃한 탄소 원자를 빨간색으로 표시하는 것을 반복하자. 이렇게 하면 빨간색으로 표시된 탄소 원자들이 주기적으로 반복되는데 이를 A부분 격자sublattice라고 하고, 파란색으로 표시된 탄소 원자들도 주기적으로 반복되는데 이를 B부분 격자라고 한다. 이렇게 탄소 원자들을 부분 격자 2개로 나눌 수 있는 것은 그래핀의 중요한 특징이다.
탄소 원자는 앞에 이야기한 것과 같이 최외각 전자 4개를 가지고 있다. 최외각 전자 4개는 2s 궤도함수에 전자 2개, 2p 궤도함수에 전자 2개이다. 탄소 원자가 모여 그래핀을 이루면 2s 궤도함수 1개와 2p 궤도함수 2개가 sp2 혼성궤도함수를 만들고 이 혼성궤도함수에 전자가 3개 들어가면서 이웃한 탄소 원자의 sp2 혼성궤도함수와 단단한 공유 결합을 형성한다. 이 공유 결합에 이용된 전자 3개는 그래핀 안에서 자유롭게 돌아다니지 못하고, 공유 결합에 사용되지 않은 전자 1개는 그래핀 안에서 자유롭게 돌아다니는 자유 전자가 된다.
그래핀 안의 자유 전자에 대해 좀더 자세히 살펴보자. 2p 궤도함수 3개 중 그래핀 면에 나란한 방향인 2px와 2py 궤도함수는 sp2 혼성궤도함수에 참여하고 그래핀 면에 수직한 2pz 궤도함수는 따로 남게 되는데, 그래핀의 자유 전자는 2pz 궤도함수에 있게 된다. 그래핀에서는 2pz 궤도함수가 모여 가전자 띠valence band와 전도 띠를 형성하는데, 그래핀의 가전자 띠와 전도 띠가 딱 두 개의 운동량에서 만나는 특이한 구조를 가지고 있다. 가전자 띠와 전도 띠가 만나는 운동량을 디락 점Dirac point이라고 부른다. 디락 점 부근에서는 전자 상태의 에너지가 운동량에 대해 1차 함수가 되어, 전자 상태의 에너지를 운동량에 대해 그리면 깔때기 모양이 되어 이를 디락 콘Dirac cone이라고 부른다.
에너지가 운동량에 비례하는 것은 빛과 같이 질량이 없는 물체, 또는 질량이 있지만 빛의 속력에 아주 가깝게 운동하는 물체의 성질이다. 그래핀에서는 전자의 속력이 광속의 약 0.3%에 불과하지만, 에너지가 운동량에 비례하는 특별한 성질을 가지고 있다. 이러한 특별한 성질은 그래핀의 탄소 원자들을 부분 격자 2개로 나눌 수 있는 것과 관련되어 있으며, 부분 격자 2개에서 전자가 가지는 물질파 위상의 차이로부터 유사 스핀pseudospin이라는 물리량을 정의할 수 있다. 유사 스핀의 방향은 디락 점 부근에서 운동량의 방향에 따라 달라진다.
그래핀의 재발견: 비틀린 이중층 그래핀
2018년 3월 미팅에서 필자와 최영우 학생을 놀라게 한 비틀린 이중층 그래핀은 그래핀 한 장 위에 다른 그래핀 한 장을 1도 정도 돌려서 겹쳐 놓은 것이다. 그래핀 2장을 방향이 똑같게 겹쳐 놓으면 그냥 이중층 그래핀이라고 부르며, [그림10]과 같이 한 장에 대해 다른 장이 회전되어 두 장의 방향에 차이가 있는 경우에 비틀린 이중층 그래핀이라고 부른다. 이렇게 그래핀 두 장이 약간 비틀려 겹쳐지면 눈에 아른아른한 모양이 생기는데 그 모양을 자세히 보면 상대적으로 밝게 보이는 부분과 어둡게 보이는 부분이 일정한 간격으로 반복되는 것을 알 수 있다. 밝게 보이는 부분은 위쪽 그래핀과 아래쪽 그래핀에서 탄소 원자가 만드는 육각형이 겹쳐지면서 육각형을 통과하는 부분이 보이기 때문에 밝게 보이는 것이고, 그렇지 않은 부분은 육각형이 겹치지 않아 약간 어둡게 보인다. 이렇게 격자 구조 두 개가 겹쳐서 큰 주기로 반복되는 구조가 나타날 때 이것을 모아레moiré 초격자라고 한다.
마법각 비틀린 이중층 그래핀: 이론적 예측과 실험적 성공
그래핀 두 장을 포개 놓으면 두 장의 그래핀 사이를 자유 전자가 옮겨 다닐 수 있게 되면서 자유 전자의 운동 상태가 영향을 받게 되는데, 2011년 미국 텍사스Texas 대학 오스틴Austin 캠퍼스의 라피 비스트리처Rafi Bistritzer 박사와 앨런 맥도널드Allan H. MacDonald 교수는 그래핀 두 장을 포개 놓을 때 어떤 특별한 경우에는 자유 전자의 속력이 0이 될 것이라 예측하였다.[34] 비스트리처 박사와 맥도널드 교수는 [그림10]과 같이 포개진 그래핀 두 장 중에 하나는 고정하고 다른 하나는 포개진 상태에서 회전시키는 경우(이렇게 하는 것을 비튼다twist라고 표현함)를 고려하였는데, 비트는 각도에 따라 자유 전자의 속력이 변하다가 어떤 특정한 각도일 때는 자유 전자의 속력이 0이 되는 것을 발견하였다. 그 각도를 마법각magic angle이라고 하였고, 마법각 중 가장 큰 각도는 1.05도로 예측되었다.[34]
이후 비튼 각도가 마법각과 같은 이중층 그래핀을 마법각 비틀린 이중층 그래핀이라 부른다. 일반적으로, 자유 전자의 속력이 0에 아주 가깝게 되면 전자의 상태 밀도가 아주 커지면서 자유 전자의 상태가 불안정해지고 특이한 상태로 상전이가 발생할 가능성이 매우 커진다. 이러한 이유로 마법각 비틀린 이중층 그래핀에서 특이한 물리 현상이 발생할 것으로 예상되었다.
마법각 비틀린 이중층 그래핀을 만들기 위해서는 그래핀 두 장의 각도 차이를 정밀히 조절할 수 있는 기술이 필요하다. 그래핀 두 장의 각도를 정확히 조절하는 기술은 2015년에 개발되었는데, 그래핀 한 장을 두 부분으로 자른 후에 한 부분을 들어 올려서 다른 부분 위에 놓는 방법으로 성공하였다.[35] 2017년에 매사추세츠 공대 하리요-에레로 교수 연구팀에서 비틀림 각도가 1.05도, 1.08도, 1.16도인 비틀린 이중층 그래핀 시료들을 제작하여 도핑에 따라 부도체적 특성과 초전도 특성이 발생하는 것을 실험적으로 발견하였다. 이러한 연구 결과들은 이 글의 맨 앞에 소개한 것과 같이 2018년 3월 미팅에 맞추어 공개되었다.[1,2]
비틀린 그래핀 다중층: 초전도 발생 원인
표준적인 초전도 이론에서는 원자의 진동이 전자와 전자 사이에 서로 끌어당기는 효과를 발생시키고, 이 효과에 의해 전기 저항이 없어지는 초전도 현상이 발생한다. 2018년 3월 미팅 직후에 최영우 학생과 함께 마법각 비틀린 이중층 그래핀에서 원자 진동의 효과가 초전도 현상을 일으킬 정도의 크기인지 연구하기로 하였다. 최영우 학생은 곧바로 비틀린 이중층 그래핀 연구를 시작하였는데, 마법각 비틀린 이중층 그래핀은 모아레 초격자 단위에 1만개가 넘는 탄소 원자가 있어서 표준적인 방법인 밀도범함수 이론density functional theory을 사용하면 계산량이 너무 커지므로 그 대신에 개별 탄소 원자를 고려하는 모델링 방법을 찾기로 하였다.
최영우 학생은 비틀린 이중층 그래핀의 원자 구조와 전자 구조에 대해 이미 확립되어 있는 모델링 방법론들을 결합하였고, 원자 진동과 전자의 상호 작용을 계산할 수 있도록 발전시켰다. 연구가 놀라운 속도로 진행되어 계산 결과를 보니, 초전도의 표준적인 발생 원인인 원자 진동의 효과가 마법각 비틀린 이중층 그래핀에서 충분히 커서, 실험에서 관측된 초전도의 발생 원인이 될 수 있었다. 즉, 비틀린 이중층 그래핀의 초전도성이 표준적인 초전도성에 가까울 수 있다는 것을 알 수 있었다. 이 연구 결과에 대해 논문을 빨리 작성하였고 2018년 9월에 학술지에 투고할 수 있었다.[36] 연구를 시작한지 단지 6개월 뒤였다.
비틀린 이중층 그래핀에서는 위상적 특성과 자성 특성도 발현되었고, 비정상 홀 현상도 실험적으로 보고되었다. 또한, 겹쳐 놓은 그래핀이 두 장인 경우뿐만 아니라 세 장인 경우와 네 장인 경우도 실험되었는데, 그래핀 세 장을 겹쳐 놓을 때 첫째 장과 셋째 장의 방향을 같게 하고 가운데에 끼인 둘째 장의 방향을 약 1.6도 어긋나게 하는 경우에 초전도가 발생하였다.[37]
최영우 학생은 비틀린 이중층 그래핀 연구 후에 그래핀이 네 장 겹쳐진 비틀린 이중 이중층 그래핀double bilayer graphene에서의 초전도 발생 가능성을 연구하였는데, 처음 예상과 달리 이중 이중층 그래핀에서는 원자 진동과 전자 사이의 상호작용이 오히려 약하여 초전도성이 발생하기 어렵다는 결과이었다. 이 결과에 대해 재검토 및 확인 작업이 이루어진 끝에, 상호작용의 강약을 결정짓는 요소를 이해하면서 계산 결과가 맞다는 결론을 낼 수 있었다.
이중 이중층 그래핀에서는 위쪽 두 장과 아랫쪽 두 장이 각각 흑연에서와 같은 버널 층쌓기Bernal stacking 구조를 가지고 있는데, 이러한 구조에서는 전자의 파동함수가 그래핀의 부분 격자 2개 중 한 개에 집중되면서 전자와 원자 진동 사이의 상호작용이 약하게 되었다. 이와 달리, 그래핀 세 장이 비틀려 겹쳐진 경우에는 비틀린 이중층 그래핀에서와 마찬가지로 전자의 파동함수가 그래핀의 부분 격자 2개에 모두 퍼지면서 전자와 원자 진동 사이의 상호작용이 매우 강하였다. 전자 파동함수의 부분 격자 대칭성이 초전도성에 큰 영향을 줄 수 있는 중요한 요소이었다.[38]
탄소 물질의 미래
위에서 필자가 소개한 탄소 나노 물질들은 공통된 특징이 있다. 탄소 원자 한 개가 주위의 다른 탄소 원자 세 개와 공유 결합을 하고 있다. 풀러렌, 탄소 나노튜브, 그래핀, 비틀린 이중층 그래핀 등이 모두 동일한 특징을 가지고 있다. 탄소 중에서도 흑연의 재발견이라 할 수 있다. 흑연의 동소체인 다이아몬드의 경우에는 탄소 원자 한 개가 주위의 탄소 원자 네 개와 공유 결합을 하고 있다. 다이아몬드의 경우에도 나노 다이아몬드 등 나노 물질 연구가 활발하다.
탄소는 우리의 생명에 아주 중요한 원소이며, 인류 문명 발전에 크게 기여하였다. 그러나 최근 탄소가 산소와 결합한 이산화 탄소가 지구 온난화의 주범으로 지목되어, 탄소 화합물을 연료로 쓰는 내연 기관 자동차가 멀지 않은 장래에 수소 자동차 또는 전기 자동차로 대체될 예정이고, 연료를 사용하지 않는 풍력 발전과 태양광 발전이 추진되고 있다. 이러한 친환경 상황에서도 탄소는 계속 중요한 역할을 담당할 것이다. 탄소 물질은 전기 자동차의 핵심 부품인 리튬이온 축전기에 중요한 요소로 사용되고 있으며, 태양광으로부터 고효율로 전기를 생산하는 페로브스카이트 물질에도 탄소를 포함한 유기물이 중요한 성분으로 사용되고 있다. 또한, 탄소를 포함한 생체 물질들은 백신 및 의약품과 관련되어 집중 연구되고 있다. 이러한 탄소 물질들은 나노미터 수준의 연구가 필요하며 미래에도 중요한 물질로서 계속 재발견 될 것이다.
참고문헌
- Unconventional superconductivity in magic-angle graphene superlattices. Y. Cao, V. Fatemi, S. Fang, Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Nature 556, 43 (2018); arXiv:1803.02342
- Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, 556, 80 (2018); arXiv:1802.00553.
- High-resolution angle-resolved photoemission studies of quasiparticle dynamics in graphite. C. S. Leem et al., Physical Review B 79, 125438 (2009).
- Graphyne: Hexagonal network of carbon with versatile Dirac cones. B. G. Kim and H. J. Choi, Physical Review B 86, 115435 (2012).
- Electric field effect in atomically thin carbon films. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Zhang, S. V. Dubonos, I. V. Grigorieva, A. A. Firsov, Science 306, 666 (2004); arXiv:0410550.
- Tunneling through a controllable vacuum gap. G. Binnig, H. Rohrer, Ch. Gerber, and E. Weibel, Applied Physics Letters 40, 178 (1982).
- Structure and dynamics of solid C60. Q.-M. Zhang, Jae-Yel Yi, and J. Bernholc, Physical Review Letters 66, 2633 (1991).
- First-principles study of the binding energy between nanostructures and its scaling with system size. J. Tao, Y. Jiao, Y. Mo, Z.-H. Yang, J.-X. Zhu, P. Hyldgaard, and J. P. Perdew, Physical Review B 97, 155143 (2018).
- C60: Buckminsterfullerene. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl, and R. E. Smalley, Nature 318, 162 (1985).
- Solid C60: a new form of carbon. W. Kratschmer, L. D. Lamb, K. Fostiropoulos, and D. R. Huffman, Nature 347, 354 (1990).
- Conducting films of C60 and C70 by alkali-metal doping. R. C. Haddon et al., Nature 350, 320 (1991).
- Superconductivity at 18 K in potassium-doped C60. A. F. Hebard, M. J. Rosseinsky, R. C. Haddon, D. W. Murphy, S. H. Glarum, T. T. M. Palstra, A. P. Ramirez and A. R. Kortan, Nature 350, 600 (1991).
- Superconductivity at 33 K in CsxRbyC60. K. Tanigaki, T. W. Ebbesen, S. Saito, J. Mizuki, J. S. Tsai, Y. Kubo, and S. Kuroshima, Nature 352, 222 (1991).
- Thermoelectric power and conductivity of the alkali metal-doped bulk fullerenes, KxC60 and NaxC60. E. B. Park, J. W. Shim, H. Park and Y. W. Park, Synthetic Metals 44, 363 (1991).
- Superconductivity at 52 K in hole-doped C60, J. H. Schön, Ch. Kloc, and B. Batlogg, Nature 408, 549 (2000). This paper was retracted in 2003.
- The origin of the anomalous superconducting properties of MgB2. H. J. Choi, D. Roundy, H. Sun, M. L. Cohen, and S. G. Louie, Nature 418, 758 (2002).
- Report of the investigation committee on the possibility of scientific misconduct in the work of Hendrik Schön and coauthors. M. R. Beasley, S. Datta, H. Kogelnik, H. Kroemer, and D. Monroe, (doi:10.1103/aps.reports.lucent) (2002).
- Band structure and Fermi surface of electron-doped C60 monolayers. W. L. Yang, V. Brouet, X. J. Zhou, H. J. Choi, S. G. Louie, M. L. Cohen, S. A. Kellar, P. V. Bogdanov, A. Lanzara, A. Goldoni, F. Parmigiani, Z. Hussain, and Z.-X. Shen, Science 300, 303 (2003).
- Helical microtubules of graphitic carbon. S. Iijima, Nature 354, 56 (1991).
- Are fullerene tubules metallic? J. W. Mintmire, B. I. Dunlap, and C. T. White, Physical Review Letters 68, 631 (1992).
- Broken symmetry and pseudogaps in ropes of carbon nanotubes. P. Delaney, H. J. Choi, J. Ihm, S. G. Louie, and M. L. Cohen, Nature 391, 466 (1998).
- New one-dimensional conductors: Graphitic microtubules. N. Hamada, S.-i. Sawada, and A. Oshiyama, Physical Review Letters 68, 1579 (1992).
- Electronic structure of chiral graphene tubules. R. Saito, M. Fujita, G. Dresselhaus, and M. S Dresselhaus, Applied Physics Letters 60, 2204 (1992).
- Electrical conductivity of individual carbon nanotubes. T. W. Ebbesen, H. J. Lezec, H. Hiura, J. W. Bennett, H. F. Ghaemi, and T. Thio, Nature 382, 54 (1996).
- Defects, quasi-bound states, and quantum conductance in metallic carbon nanotubes. H. J. Choi, J. Ihm, S. G. Louie, and M. L. Cohen, Physical Review Letters 84, 2917 (2000).
- Going beyond the mean-field approximations of alloys and alloy superlattices: a few puzzles solved? D. S. Kim et al., Journal of the Optical Society of America B 13, 1210 (1996).
- Ab initio pseudopotential method for the calculation of conductance in quantum wires. H. J. Choi and J. Ihm, Physical Review B 59, 2267 (1999).
- Two-dimensional gas of massless Dirac fermions in graphene. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov, Nature 438, 197 (2005); arXiv:0509330.
- Experimental observation of the quantum Hall effect and Berry's phase in graphene. Y. Zhang, Y.-W. Tan, H. L. Stormer, and P. Kim, Nature 438, 201 (2005); arXiv:0509355.
- Letter to the 2010 Nobel Committee. W. de Heer, (2010).
- 그래핀. 손영우, 물리학과 첨단기술 2008년 10월호 40쪽.
- The electronic properties of graphene. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, Review of Modern Physics 81, 109 (2009); arXiv:0709.1163.
- Theory of emergent Josephson lattice in neutral twisted bilayer graphene. G. Baskaran, arXiv:1804.00627.
- Moiré bands in twisted double-layer graphene. R. Bistritzer and A. H. MacDonald, PNAS 108, 12233 (2011).
- van der Waals heterostructures with high accuracy rotational alignment. K. Kim et al., Nano Letters 16, 1989 (2016).
- Strong electron-phonon coupling, electron-hole asymmetry, and nonadiabaticity in magic-angle twisted bilayer graphene. Y. W. Choi and H. J. Choi, Physical Review B 98, 241412 (2018).
- Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. J. M. Park, Y. Cao, K. Watanabe, T. Taniguchi, and P. Jarillo-Herrero, Nature 590, 249 (2021).
- Dichotomy of electron-phonon coupling in graphene moiré flat bands. Y. W. Choi and H. J. Choi, Physical Review Letters 127, 167001 (2021).