온도와 양자역학
아이작 뉴턴Isaac Newton, 1642-1726이 정립한 역학은 당대의 가장 큰 문제였던 천체 운동을 설명하는 데 있어 대단히 성공적이었다. 19세기 중반에는 제임스 맥스웰James Maxwell, 1831-1879이 전자기장의 운동을 맥스웰 방정식 형태로 정리해 발표하면서, 물리학자들은 다른 학문 분야에서는 찾아보기 드문 보편적 법칙universal law에 기반한 세계관을 공유하게 되었다. 뉴턴의 역학과 맥스웰의 전자기학으로 대표되는 고전 물리학이 19세기 말과 20세기 초에 접어들어 여러 방향에서 동시다발적으로 허점을 노출하기 시작했고, 그 결과 상대성이론과 양자역학이 등장했다.
양자역학이라고 하면 흔히 원자 같은 미시적인 개체에만 적용되는 물리 법칙이라고 생각하기 쉽다. 위키피디아는 양자역학을 ‘원자나 그보다 작은 입자들의 자연 현상을 기술하기 위한 물리학 이론’이라고 정의하고 있다. 그러나 막상 양자역학 이론이 가장 먼저 성공적으로 적용된 사례는 우리 눈에 보이는 거시적인 물체가 내뿜는 빛의 스펙트럼 밀도(파장에 따라 방출되는 빛의 양을 표현하는 물리량)를 이론적으로 설명한 막스 플랑크Max Planck, 1858-1947의 흑체 복사 법칙이니, 거시적인 물체라고 해서 양자역학이 적용되지 않는 것은 아니다. (플랑크의 흑체 복사 법칙이 무엇인지 궁금한 사람들은 “[과학의 결정적 순간들] 1900년 베를린, 플랑크의 ‘양자 혁명’”과 “양자 물질의 역사 [7]: 빛도 물질이다”를 참고하자.) 다만 흑체 복사의 경우를 제외하면 일상에서 양자역학적 효과가 눈에 잘 띠지 않을 뿐이다.
왜 그럴까? 이를 이해하기 위해 ‘상자 안의 입자a particle in a box’라고 부르는 간단한 양자 역학 문제를 하나 풀어보자. 평평한 1차원 공간의 양 끝에 벽을 세워놓고, 입자 한 개를 그사이에 넣는다. 두 벽 사이에서 운동하는 입자의 에너지는 고전 물리학에 따르면 아무 에너지나 다 가능하다. 입자는 두 벽 사이에서 임의의 속력 \(v\)로 왕복 운동을 할 수 있고, \(\frac{1}{2}mv^{2} \)으로 주어지는 운동 에너지를 갖는다.
양자역학적인 답은 사뭇 다르다. 양자역학적 입자는 벽 사이를 단순 왕복 운동을 하는 대신에 특정 위치에서 발견될 확률 분포로 존재한다. 이 확률 분포를 기술하는 것이 양자역학의 파동 함수이고, 입자의 상태를 파동 형태로 표시할 수 있다는 게 바로 입자-파동의 이중성이다.
꽉 막힌 벽 사이에 존재하는 입자의 파동 함수를 풀어보면 [그림1]과 같이 양쪽이 고정된 고무줄의 진동 형태와 같은 모양이 나온다. 고무줄의 길이가 \(L\)이라고 하면, 파장의 길이가 \(2L, \frac {2L}{2}\),\(\frac {2L}{3}\),\(\frac {2L}{4}\),…즉, 길이 \(2L\)을 정수로 나눈 파장의 정상파 형태만 존재 가능하다. 불연속적인 파장의 파동만 상자 속에 존재할 수 있다는 건 (파동-입자의 이중성에 따라) 입자가 가질 수 있는 에너지 역시 띄엄띄엄, 불연속적임을 의미한다. 상자의 크기, 즉 \(L\)이 작아질수록 입자가 가질 수 있는 에너지 값 사이의 간격이 커진다는 점도 양자역학의 특징이다.
띄엄띄엄한 양자역학적 에너지 준위의 효과가 드러나게 하려면 어떤 조건이 필요할까? 여기서 등장하는 중요한 고려 대상이 바로 온도다. 모든 물리학적 대상(‘물리계’라고 부른다)은 주변 환경과 상호작용 할 수밖에 없는데, 상호작용 중 하나는 주변 환경과 에너지를 주고받는 일이다. 물리계가 주변 환경과 주고받는 에너지의 양은 온도가 높을수록 많아진다. 절대 온도 \(T\)에 비례하는 열적 에너지의 교환이 일어난다. 온도가 아주 낮을 때는 주변 환경으로부터 받아들이는 에너지의 양도 적다 보니 입자는 물리계가 허용하는 양자역학적 에너지 준위 중 가장 낮은 몇 개 정도만 점유하게 된다.
반면 온도가 아주 높아지면 물리계의 에너지도 덩달아 높아지면서 수많은 양자역학적 에너지 준위에 입자들이 골고루 분포한다. 매우 많은 양자역학적 에너지 준위에 입자가 다 차 있다 보면 에너지 준위 하나하나의 정확한 값은 더이상 중요하지 않고, 에너지 준위가 불연속적이란 사실도 큰 의미가 없다. 작은 가구를 조립할 때는 1mm의 오차도 허용이 안 되겠지만 커다란 건축물을 세울 때는 그 정도 차이를 무시할 수 있는 것과 비슷한 이치다.
물리학자가 온도가 낮은지 높은지 판단하는 기준은 결국 온도에 따른 열적 에너지와 물리계가 갖고 있는 고유한 양자역학적 에너지 준위의 간격을 비교함으로써 얻을 수 있다. 예를 들어 원자 속 전자가 갖는 에너지 준위의 차이는 대략 수백mm 전자 볼트지만 상온인 300K에 해당하는 열적 에너지는 이보다 열 배쯤 작다. 그렇기 때문에 상온에서도 원자 속 전자의 개별적 에너지 준위로 인한 양자역학적 현상은 중요하다. 우리가 일상에서 보는 물건이 다 뚜렷한 색깔을 가질 수 있는 이유도 이와 무관하지 않다. 훨씬 뜨거운 온도에서는 전자가 온갖 종류의 에너지 준위를 다 가질 수 있기 때문에 에너지 차이도 제각각, 따라서 원자가 방사하는 빛의 색깔로 제각각이 될 것이고 세상은 온통 무지개빛(?)으로 변할 것이다.
물리계의 크기가 커짐에 따라 양자역학적 에너지 준위 사이의 간격이 줄어들고 매우 많은 양자역학적 에너지 준위가 물질의 거동에 관여하게 되기 때문에 개별적인 에너지 준위의 의미와 중요성이 사라진다. 온도가 높다고 해서 물질이 갖고 있는 양자역학적 본질 자체가 달라지는 것은 아니지만, 우리가 관측할 수 있는 물성이나 물질의 거동에서는 그 모습을 드러내지 않게 된다.
이런 거시적인 물리계의 양자역학적 현상을 복구하기 위해서는 온도를 낮춰야만 한다. 그런 의미에서 이전 글 “액체의 재발견 [1]: 액화의 역사”에 소개했던, 세상에 존재하는 모든 기체를 액체로 만들고자 했던 한 무리의 과학자들은 양자역학에 대해 아무것도 몰랐지만 결과적으로 양자역학적 비밀을 풀어낼 단초를 제공한 셈이다. 헬륨 기체를 액화하는 데 성공한 카멜링 온네스는 거시적 물리계에서 나타나는 양자역학적 현상을 두 가지나 발견하였는데, 그중 하나가 초전도체이고 다른 하나는 얼지 않는 액체다.
저항이 없는 도체
초전도체는 영어 “superconductor”를 직역한 용어로 최고의 전도체conductor, 즉 전기 저항이 전혀 없는 전도체를 말한다. 온네스가 이를 발견한 과정은 우연과 행운으로 가득 차 있다. 그 당시는 절대 영도란 개념이 정립된 지 얼마 안 된 시기였고 도체의 온도를 절대 영도에 가깝게 낮추면 전기 저항이 어떻게 변할지가 학계의 주요 관심사였다. 이에 대해 크게 세 가지 예측이 있었는데 우선 실험적 관측을 바탕으로 아우구스투스 매티슨Augustus Matthiessen, 1831-1870이 제안했던 매티슨 규칙Matthiessen’s rule이 있다.
매티슨 규칙의 핵심은 고체의 저항값 중 일부는 고체 자체의 내재적 특성으로 결정되지만, 고체 속에 섞여 들어간 불순물impurities과 결함defects이 결정하는 부분이 있다는 것이다.1 도체 내의 전자들끼리 서로 충돌하여 발생하는 순수한 도체의 전기 저항은 온도를 낮추다 보면 점점 줄어들더라도, 불순물과 결함은 온도를 낮춘다고 새로 생겨나거나 사라지지 않기 때문에 이로 인한 전기 저항은 온도와 무관할 것이다. 따라서 실제 금속처럼 불순물이나 결함이 존재하는 불완전한 물질은 아주 낮은 온도에서도 불순물과 결함으로 인한 저항이 남아 있을 것이라는 게 매티슨의 생각이었다.
반면 제임스 듀어James Dewar, 1842-1923(수소 액화에 최초로 성공한 바로 그 듀어다!)는 매티슨 규칙이 적용되지 않는 도체를 만들 수 있을 것이고 온도를 충분히 낮추면 전기 저항도 결국 완벽히 사라질 것이라고 생각했다. 그와 정반대로 켈빈 경William Thomson, 1st Baron Kelvin, 1824-1907처럼 온도를 낮추면 도체 내의 전자들도 얼어붙어서 고체가 될 것이고, 그러면 전자가 움직일 수 없으니까 전기 저항이 오히려 커져야 한다고 생각한 이들도 있었다.
각각의 주장은 충분히 그럴듯했고, 온네스는 세상에서 가장 낮은 온도에 도달할 수 있는 기계를 갖고 이런 문제에 도전해볼 특권을 갖고 있었던 셈이다. 전기 전도도가 좋기로 잘 알려진 구리, 금, 은이나 귀금속인 백금으로 실험을 했을 때에는 매티슨 규칙을 벗어나지 않는 결과를 얻었다. 듀어가 상상했던 완전무결한 금속이나 켈빈이 상상했던 전자가 고체로 얼어버리는 물질의 상태는 존재하지 않는 듯했다.
1911년 수은을 이용하여 실험을 하였더니 아무도 상상 못 한 일이 벌어졌다. 섭씨 −269도(흥미롭게도 헬륨의 액화하는 온도와 매우 비슷하다)에서 갑자기 전기 저항이 정확히 0으로 떨어지는 현상이 관측되었다. 최초의 초전도체 발견이었다. 왜 하필 수은이었을까? 수은은 전기 전도도가 특별히 좋은 금속도 아니었다. 게다가 수은은 상온에서 액체 상태로 존재하기 때문에 유리관에 액체 수은을 담아서 저온 실험을 수행해야 하는데, 냉각 과정에서 유리관이 수축하다가 그만 깨질 수도 있고, 진공을 만드는 과정에서 유리관 속의 수은 증기가 새어나올 여지도 있었다. 애초에 고체로 존재하는 다른 금속에 비해 훨씬 실험이 난해함에도 불구하고 굳이 수은을 선택한 이유는 무엇이었을까?
매티슨 규칙과 듀어의 주장 사이에 그 답이 숨어 있다. 매티슨 규칙이 가정한 불순물 효과를 제거하려면 금속에 섞여 있는 불순물을 줄여야 한다. 이에 대한 온네스의 응답은 녹는점이 낮은 금속을 이용하자는 것이었다. 금속을 정제(불순물을 제거)하려면 우선 금속을 녹여야 하는데 녹는 점이 높은 금속은 용해 과정에서 필연적으로 산소 등의 기체가 녹아 들어간다. 뒤집어 말하면, 다른 물질은 녹지 않는 온도에서 이미 액체 상태로 존재하는 금속이라면 상대적으로 정제가 쉽고, 높은 순도의 금속을 얻을 수 있다는 논리였다. 매티슨 규칙을 벗어날 수 있는 가장 유리한 물질은 상온에서도 액체 상태로 존재하는 유일한 금속, 수은이었다!
이렇게 선택된 수은의 초전도 발현 온도가 하필 섭씨 −269도였던 것 역시 행운이 아닐 수 없다. 단일 원소로 된 금속 중 대기압에서 초전도 현상이 나타나는 물질은 29가지가 있는데, 이 중에서 15개의 물질은 초전도 발현 온도가 −271도보다 낮아서 그 당시의 온네스조차 도달할 수 없었던 온도다. 수은은 29가지 물질 중 초전도 발현 온도가 다행히도 8번째로 높은 물질이니, 다른 많은 중요한 발견과 마찬가지로 우연에 우연이 겹쳐 초전도체의 발견이 이뤄진 셈이다. 수은의 초전도 발현 온도가 조금만 더 낮았더라면 초전도체 발견은 훨씬 더 뒤로 미뤄졌을지도 모를 일이다. 초전도체에 대해서는 향후에 ‘초전도체의 재발견’을 통해 자세히 소개될 예정이니 본 글의 주제인 액체 이야기로 다시 돌아가 보자.
얼지 않는 액체
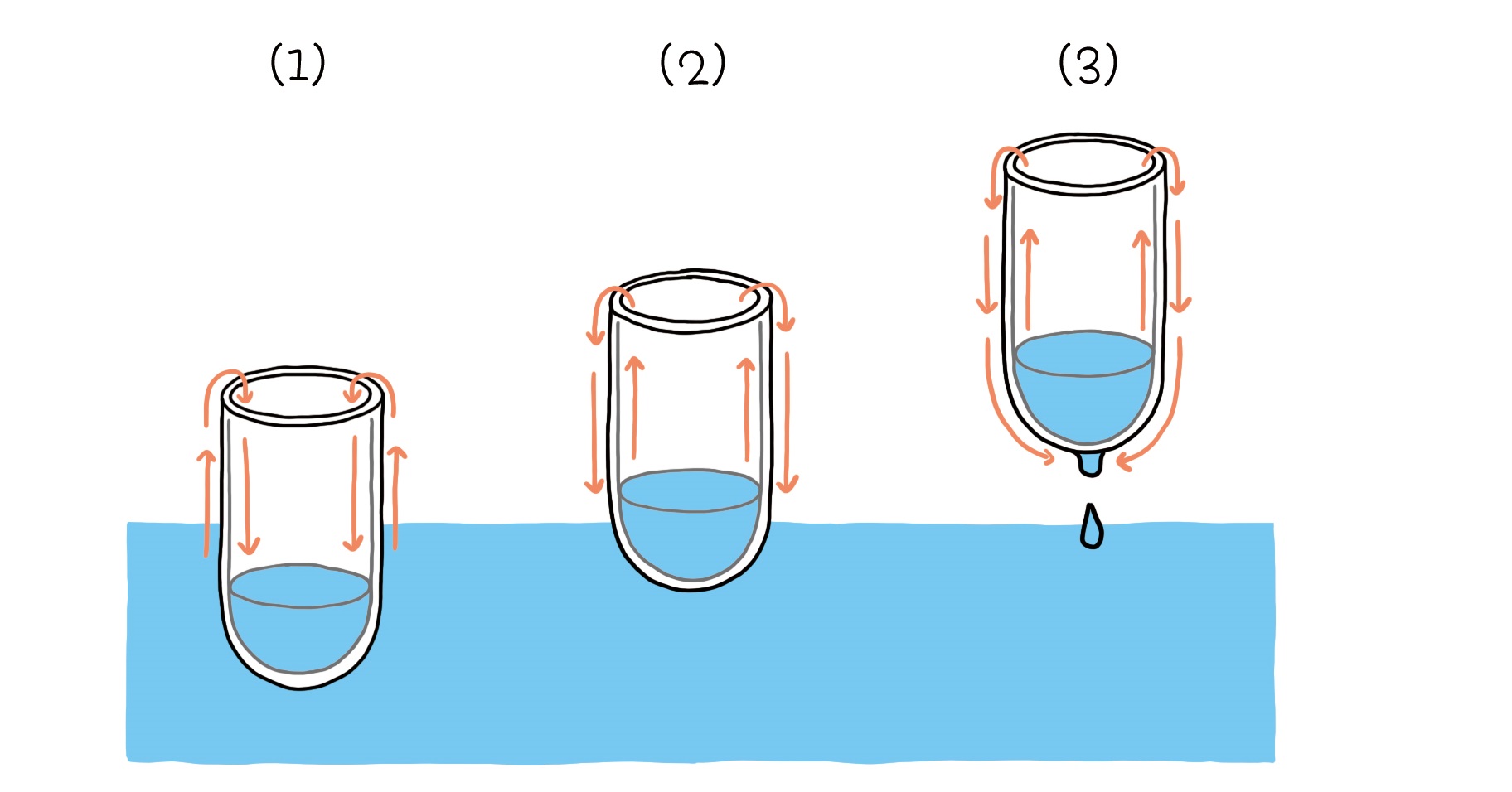
모든 기체는 충분히 차갑게 만들면 액체로 변한다. 마찬가지로 모든 액체는 충분히 차갑게 만들면 고체로 변한다. 하지만 액체 헬륨의 온도를 아무리 낮춰도 여전히 고체 헬륨이 만들어지지 않는다. 비록 영구 기체는 자연에 존재하지 않지만 영구 액체는 존재하는 셈이다. 초전도체 발견에는 온네스의 ‘다른 관심사’가 중요한 역할을 했다. 수은의 초전도 발현 온도는 액체 헬륨의 액화점 온도와 거의 같기 때문에 헬륨을 액화점 이하로 충분히 낮춰야만 수은의 저항이 0으로 떨어지고, 계속 저항이 0인 상태를 안정적으로 유지한다는 사실을 확인할 수 있다.
이런 극저온 실험이 가능했던 이유는 온네스가 액체 헬륨을 ‘얼리는’ 일에 관심을 가졌기 때문이다. 다른 모든 물질과 마찬가지로 헬륨도 기화 냉각을 하다 보면 액체-기체 공존선을 따라 가다 삼중점을 만나 얼어붙을 것이란 것이 온네스의 예측이었다. 공교롭게도 −271도 아래로 온도를 내려도 헬륨은 얼지 않았다. 하지만 그 덕분에 −269도 아래로 충분히 냉각을 할 장치를 얻었고 수은의 초전도 현상도 발견할 수 있었다.
온네스가 발견한 얼지 않는 헬륨의 이면에는 중요한 특성이 숨어 있다. 우주에 존재하는 물질 중 절대 영도까지 온도를 낮춰도 얼지 않는 유일한 물질이 헬륨이다. 헬륨이 이토록 특이한 성질을 가질 수 있는 건 두 가지 조건이 맞아떨어지기 때문이다. 하나는 주기율표에서 두 번째로 등장하는 매우 가벼운 원자가 모여 만들어졌다는 점, 다른 하나는 주기율표 가장 우측 열에 존재하는 비활성 물질, 즉 원자와 원자 사이의 상호작용이 매우 약한 물질이란 점이다.
양자역학의 불확정성 원리로 인해 입자는 가장 낮은 에너지 상태에서도 가만히 있지 못하고 영점 운동zero-point motion이란 것을 한다. 헬륨 원자는 매우 가볍다 보니 양자역학적인 영점 운동이 매우 큰 반면 원자간 상호작용은 작아서 영점 운동을 구속할만한 다른 힘이 없다. 그 결과 절대영도에서조차 헬륨 원자들을 제자리에 묶어둘 수가 없고 고체 대신 액체 상태로 존재한다. 양자역학적 특성인 영점 운동이 절대영도 근방의 특성을 지배하는 액체라는 의미로 액체 헬륨을 양자 액체 또는 양자 유체라고 한다. (헬륨이 절대로 고체가 되지 않는다는 뜻은 아니고, 절대영도에서 약 30기압의 높은 압력을 가해서 헬륨 원자의 영점운동을 강제로 억제하면 고체로 만들 수 있다.)
양자 액체의 특성은 단순히 절대영도에서도 고체가 되지 않는다는 사실에 그치지 않았다. 액화를 통해 헬륨을 절대온도 4.2K까지 냉각하는 데 성공한 온네스는 기화 냉각을 통해 온도를 더욱 낮추면서 액체 헬륨의 밀도와 유전율, 비열 등 다양한 특성을 측정하였다. 그 과정에서 특이한 현상을 관측하였는데 이런 물리량이 모두 절대온도 2.2K 근방에서 뾰족한 최대값을 가진다는 점이었다. 온네스는 이게 특이하다고 생각했고, 빌렘 키솜Willem Keesom, 1876-1956과 미에치스와브 볼프케Mieczysław Wolfke, 1883-1947는 액체 헬륨이 이 온도에서 모종의 상전이를 거친다는 결론을 내렸다.
그렇지만 이미 액체가 되어버린 헬륨이 또 다른 액체로 상전이 한다는 게 어떤 의미인지 정확히 파악하지 못했고 그저 막연하게 상전이 온도 위의 액체를 헬륨 I, 그 아래 온도에 존재하는 액체를 헬륨 II라고 불렀다. 비열의 경우 상전이 온도 근방에서 거의 발산하다시피 급격히 증가하는 양상을 보이는데, x축을 온도, y축을 비열로 놓고 그린 그래프의 개형이 그리스 문자 람다\(λ\)를 닮았다고 하여 액체 헬륨의 상전이 온도를 람다점\(\lambda\) point이라고도 한다.
그다음 질문이 무엇인지는 사실 자명하다. 2.2K에서 과연 무슨 일이 벌어지는 걸까? 이에 대한 정확한 해답을 주는 건 아니지만, 한 가지 단서를 주는 개념이 드브로이의 물질파 개념이다. 광전효과를 통해 빛에 대한 입자-파동의 이중성이 증명된 이후에, 루이 드브로이Louis de Broglie, 1892-1987는 빛만이 아니라 물질도 입자와 파동의 이중성을 띌 수 있다고 제안하였다. 호기심 많은 독자를 위해 물질파의 파장을 계산하는 공식을 소개하면 \(\lambda_{th}= \sqrt{ \frac{2 \pi \hbar^2}{mk_BT} } \)이다.
온도가 낮아질수록 드 브로이의 물질파장이 길어진다. 액체 헬륨을 구성하는 헬륨 원자 사이의 평균 거리를 이 파장과 비교해 볼 수 있다. 온도가 높으면 입자간 거리에 비해 드브로이 물질파가 짧기 때문에 물질의 파동성에 기반한 양자역학적 특성을 고려하지 않아도 된다. 하지만 온도가 낮아지면 드브로이 파장이 길어지면서 입자간 거리와 비슷해지거나 이보다 길어지게 되고 물질의 특성을 기술할 때 양자역학이 중요해진다.
글의 초반에 물질의 에너지 준위를 예로 들면서 온도가 낮을수록 물질의 양자역학적 특성이 중요해진다고 한 주장과도 일맥상통한다. 드브로이 물질 파장의 공식에 헬륨 원자의 질량값을 대입해보면 약 3K에서 드브로이 물질파장이 액체 헬륨의 헬륨 원자간 거리와 비슷해진다. 이로부터 2.2K에서 나타나는 액체 헬륨의 상전이가 액체 헬륨의 양자역학적 특성이 중요해지기 때문에 벌어지는 현상일 것이라고 짐작할 수 있다.
헬륨 II의 정체가 제대로 밝혀진 것은 1937년이다. 모스크바에 있는 물리 문제 연구소Institute for Physics Problems의 수장 표트르 카피차Pyotr Kapitsa, 1894-1984와 토론토 대학의 존 앨런John F. Allen, 1908-2001과 도날드 마이즈너Donald Misener, 1911-1996가 독립적으로 좁은 틈을 통해 액체 헬륨을 통과시키는 실험을 했고 2.2K 이하의 온도에서는 액체 헬륨의 점성이 사라진다는 사실을 알아냈다. 저항이 없이 흐를 수 있는 액체를 발견한 것이다!
저항이 없다는 점이 초전도체와 닮았다고 생각한 카피차는 이를 초유체superfluid라고 불렀다. 관점에 따라서는 온네스의 연구실에서 초전도체와 초유체를 모두 발견하였다고 볼 수도 있지만, 역사는 온네스가 그 발견의 씨앗을 심은 것으로 간주하고 있을 뿐, 실제 발견의 공로는 카피차와 알렌, 마이즈너의 몫으로 기록하고 있다. 다만 노벨 위원회의 생각은 조금 달랐는지 1978년 카피차에게만 노벨상을 수여하였다. (카피차의 단독 수상은 아니었고, 다소 엉뚱하게도 우주 배경 복사를 발견한 아르노 펜지어스Arno Penzias, 1933-현재와 로버트 윌슨Robert Wilson, 1936-현재과의 공동 수상이었다.)
카피차가 초유체를 발견하게 된 과정도 흥미롭다. 올해로부터 정확히 100년 전인 1921년 스페인 독감으로 아내와 두 아이를 잃은 카피차는 영국 캠브리지 대학으로 건너가서 어니스트 러더포드Ernest Rutherford, 1871-1937와 일을 시작한다. 카피차는 캠브리지에서 세계 최초의 펄스 자석을 개발하는 등 실험에 남다른 재능이 있었다. 1934년 소련에 일시 귀국했던 카피차는 소련 정부의 출국금지 명령에 따라 영국으로 돌아가지 못하고 소련에 남게 된다. 그를 출국금지 시킨 소련 정부는 물리 문제 연구소를 설립하고 카피차를 소장으로 임명했으니 그의 능력을 조국이 충분히 알아본 셈이다. 다만 영국에서 하던 연구를 계속할 만한 시설이 없었기 때문에 연구 분야를 바꿔야만 했는데, 카피차가 새로 선택한 게 액체 헬륨을 연구하는 저온 물리학이었다. 그 결과 노벨상까지 받았으니 카피차로서는 인생만사 새옹지마란 생각을 했을 듯하다.
초유체 현상은 왜 나타날까? 헬륨 원자를 찬찬히 뜯어보자. 일단 헬륨 원자 속에는 원자핵과 두 개의 전자가 있다. 헬륨의 원자핵은 다시 양성자 두 개, 중성자 두 개로 구성된다. 전자와 양성자, 중성자는 스핀 값이 \(\frac {1}{2}\)인 입자다. 여섯 개의 스핀 \(\frac {-1}{2}\) 입자가 모여서 만들어진 헬륨 원자의 총 스핀은 0이다. (\(\frac {1}{2}\)을 여섯 개 더했는데 왜 0이 나올까 궁금하다면 양자역학 교과서를 공부해보도록 추천한다.) 입자의 스핀이 0, 1, 2 같은 정수로 주어지는 입자를 보즈Bose 입자 또는 보손boson이라고 하고, 입자의 스핀이 반정수\((\frac {1}{2}, \frac {3}{2}, \frac {5}{2},…)\)로 주어지는 입자를 페르미 입자 또는 페르미온이라고 한다. 페르미온은 “양자 물질의 역사 [3]: 파울리 호텔”에 소개된 파울리의 배타 원리를 따르는 데 반해서 보존은 같은 양자 상태에 들어갈 수 있는 입자의 개수에 제한이 없다.
다수의 보손으로 구성된 물질의 온도를 서서히 낮추다 보면 어떤 일이 벌어지는지 한번 생각해 보자. [그림4]와 같이 무한히 많은 에너지 상태에 유한한 개수의 입자를 집어 넣어 보자. 아주 온도가 높아서 입자들이 충분한 열에너지를 가질 수 있다면, 입자들은 수많은 에너지 상태에 골고루 분포할 수 있다. 이때는 입자들이 점유할 수 있는 에너지 상태의 수가 입자수보다 많으므로 각 에너지 상태에는 평균적으로 1개 이하의 입자가 들어간다. 반면에 절대영도에서는 물질이 자신에게 허용된 가장 낮은 에너지 상태에 있어야 한다. 보손은 같은 에너지 상태에 들어갈 수 있는 입자 수의 제한이 없으므로 모든 입자들이 동일한 상태에 옹기종기 모여있을 것이라 쉽게 상상할 수 있다.
신기한 일은 지금부터 벌어진다. 온도를 낮추면서 보손 입자가 차츰차츰 기저 상태로 내려오는 게 아니다. 일정 온도까지는 높은 에너지의 보손 입자들이 점진적으로 낮은 에너지 상태를 찾아가는 게 맞지만, 특정 온도 이하로 내려가는 순간 대부분의 보손 입자가 기저 상태로 급격하게 모여드는 현상이 벌어진다. 이는 기체의 액화 현상과도 유사하다. 기체를 압축하다 보면 특정 압력에서 기체 입자들이 갑자기 서로 뭉치기 시작하면서 액체로 바뀐다. 이를 기체-액체 상전이라고 했다. 물질의 밀도가 작은 상태(기체)에서 큰 상태(액체)으로 불연속적으로 바뀌는 것처럼, 기저 에너지 상태를 차지하는 입자의 밀도가 작은 상태에서 큰 상태로 불연속적으로 변한다. 이런 변화 역시 물질의 상전이 현상으로 이해할 수 있다.
이런 가능성을 이론적으로 제안한 사람은 다름 아닌 사티엔드라 보스Satyendra Bose, 1894-1974와 알베르트 아인슈타인Albert Einstein, 1879-1955이고, 이들의 이름을 따서 이 현상을 보스-아인슈타인 응축 현상이라고 한다. 초유체 현상이 보고된 지 얼마 지나지 않아 프릿츠 런던Fritz London, 1900-1954은 액체 헬륨이 보스-아인슈타인 응축을 거치며 나타내는 한 가지 증상이 초유체 현상임을 알아냈다.
점성이 없는 액체는 우리 주변에서 좀처럼 관찰할 수 없다는 점에서 대단히 독특하고 신기하지만, 고전적인 유체 이론만 보더라도 점성이 없는 액체는 얼마든지 기대할 수 있었다. 초유체가 보즈-아인슈타인 응축에 의한 양자유체라는 보다 확실한 증거는 없을까? 물론 저온에서는 거시적인 물질도 양자역학의 지배를 받을 수 있다거나, 드브로이 물질파장이 원자 사이의 간격과 비슷해지는 온도가 하필 초유체 현상이 발현되는 온도와 비슷하다거나, 헬륨 원자는 보손이므로 보스-아인슈타인 응축 상전이 현상이 일어날 수도 있다는 등의 정황 증거는 많지만 초유체 헬륨이 보스-아인슈타인 응축에 의한 양자역학적 상전이라는 직접적인 증거라고 보기에는 무리일 수도 있다. 추후에 이에 대한 실험 증거들이 속속들이 모였지만, 본 글에서는 그중에서도 가장 중요한 특성 한 가지만 이야기해 보자.
초유체가 보즈-아인슈타인 응축에 의한 현상이라면 초유체를 구성하는 입자인 헬륨 원자들은 모두 동일한 기저 상태에 모여 있을 것이다. 이 기저 상태를 기술하는 파동 함수가 있다면, 이 한 개의 파동 함수로 시스템을 기술하는 것이 가능하다. (양자역학적 파동 함수에 대해 보다 자세히 알고 싶은 독자들은 “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”을 참조하자.) 이렇게 파동 함수 한 개로 초유체를 표현하게 되면 나타나는 중요한 특징 중 하나는, 액체를 회전시킴에 따라 소용돌이가 점진적으로 커지는 대신에 용기의 크기와 모양에 따라 결정되는 특정 회전 속도의 정수배가 될 때마다 소용돌이의 회전량 역시 \(\frac {h}{m}\)의 정수배로 커진다는 것이다. 즉, 액체의 회전이 양자화된다.
이 아이디어를 처음 제시한 사람은 라르스 온사거Lars Onsager, 1903-1976였는데, 곧이어 리처드 파인만Richard Feynman, 1918-1988은 초유체에서는 한 개의 소용돌이가 \(\frac {h}{m}\)의 정수(\(n\))배의 회전량을 갖는 대신에 정확히 \(\frac {h}{m}\)의 회전량을 갖는 \(n\)개의 단위 소용돌이로 조각날 것이라는 예측을 내놓았고, 이를 양자 소용돌이라고 한다. 양자 소용돌이는 1979년에 버클리 대학의 물리학자들에 의해 실험적으로 검증되었다. 거시적인 양자 파동함수 한 개로 기술할 수 있는 물질 상태로서의 초유체가 실험적으로 명백하게 확인된 순간이었다. 온도를 낮추다보면 ‘우리가 전혀 알지 못하는 새로운 액체’가 나타나리라 상상했던 라부아지에조차도 이런 액체를 상상하지는 못했을 것이다.
세상에서 가장 신기한 액체
이쯤에서 새롭고 신기한 액체를 찾아나가던 우리의 여정이 끝을 향해 가고 있다고 느끼는 독자도 있을 것이다. 그렇지만 자연은 한 가지 비밀을 더 숨겨두고 있었는데, 그것은 헬륨의 동이원소 중 하나인 헬륨-3이다. 우리에게 익숙한 헬륨-4의 원자핵은 앞서 이야기한 바와 같이 양성자 2개, 중성자 2개로 이루어져 있어서 질량수 4를 갖는다. 여기서 중성자를 하나 뺀 것이 질량수 3의 동위 원소인 헬륨-3이다.
대기의 성분을 보면 헬륨-4는 대기 분자 백만 개 중에 5개 정도에 불과하다. 그런데 헬륨-3의 비율은 그보다도 백만배 이상 낮아서, 대기 분자 1조개 중에 1개 정도이다. 당연히 발견이 쉽지 않았고, 1939년이 되어서야 그 존재가 처음으로 확인되었다. 제2차 세계대전 중 원자폭탄을 개발하는 과정에서 삼중수소가 방사성 붕괴를 하면 헬륨-3가 된다는 사실이 밝혀지면서 인위적인 생산이 가능해졌다. 이런 이유로 다량의 헬륨-3에 대한 연구는 1947년부터 본격적으로 시작되었다.
액체 헬륨-4도 충분히 신기하지만, 동위원소인 헬륨-3 원자로 액체를 만들면 더욱 이상한 일이 벌어진다. 몇 가지 예를 들자면, 저온고압에서 액체 헬륨-3의 온도를 올리면 고체 헬륨-3이 된다. 보통 액체에는 오직 종파의 진동만 존재할 수 있는데 헬륨-3은 액체임에도 불구하고 횡파가 진행할 수 있다. 뿐만 아니라 액체 헬륨-3 속에는 입자와 반입자를 구분할 수 없는 마요라나 입자2가 존재하기도 한다. 헬륨-3를 평생 연구해온 필자의 주관적인 의견이긴 하지만, 자연이 인류에게 마지막까지 숨겨 두었던 액체인 헬륨-3은 이 세상에서 가장 신비로운 액체다.
이 모든 신비로움은 헬륨 원자핵에 들어간 중성자 개수 하나 때문에 벌어진다. 헬륨-4는 보손이지만 여기서 중성자가 하나 빠진 헬륨-3 원자는 페르미온이다. 보손과 페르미온을 지배하는 양자역학은 근본적으로 다르다. 보손은 동일한 양자역학적 상태를 동시에 점거할 수 있는 입자 수에 제한이 없지만 페르미온은 동일한 양자역학적 상태에 두 개 이상의 입자가 들어갈 수 없다. 아주 높은 온도에서는 어차피 입자들이 수많은 에너지 상태에 골고루 퍼지면서 각 에너지 상태를 점거하는 입자수가 어차피 한 개 미만이기 때문에 보손과 페르미온의 차이가 드러나지 않는다. 하지만 온도가 낮아지면 상황이 전혀 달라진다. 높은 온도에서 잘 드러나지 않던 양자역학적 특성이 온도가 낮아지면서 두드러지는 현상이 헬륨-3과 헬륨-4 액체의 성질 차이에서 다시 한 번 드러난다.
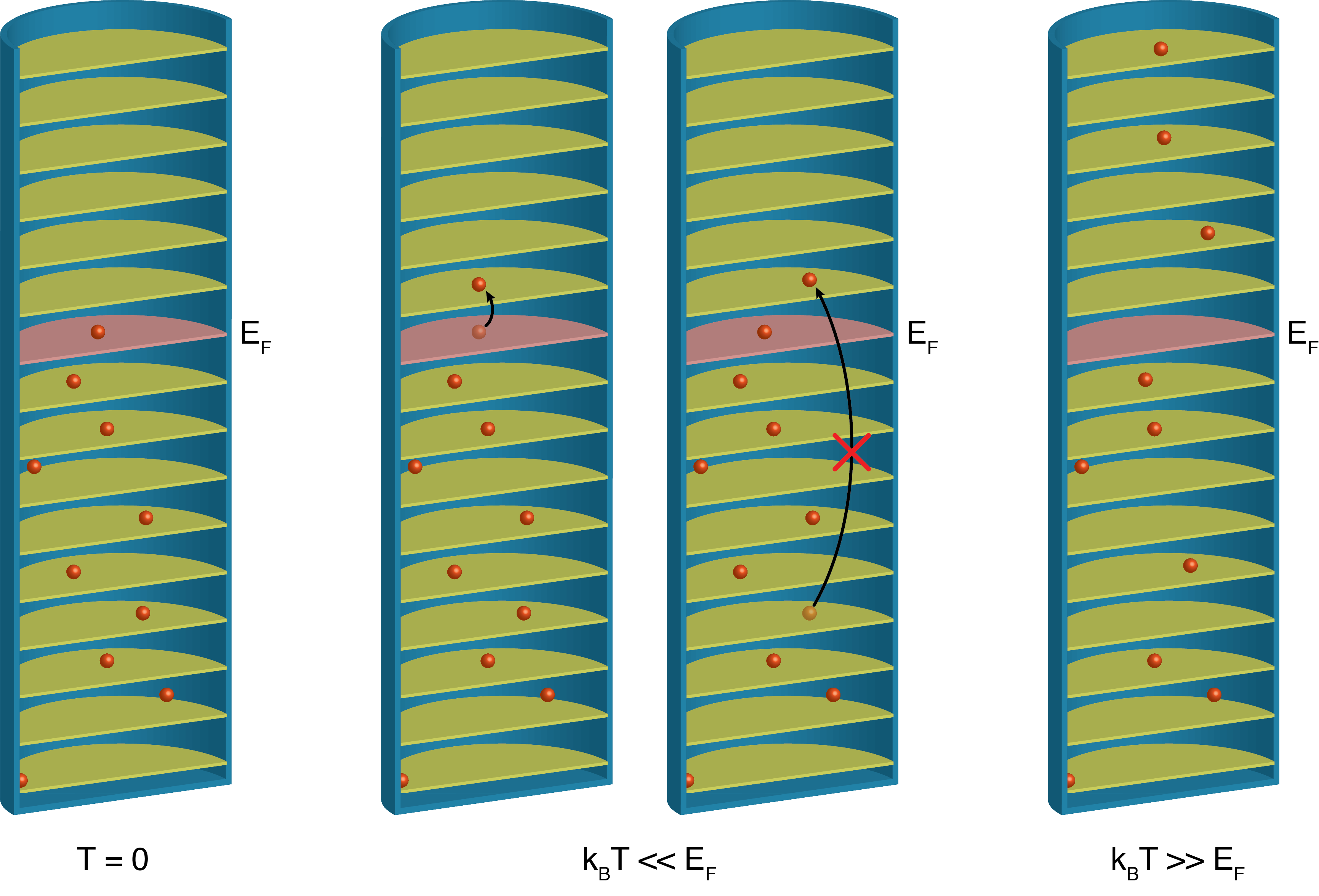
절대영도 근방에서 정확히 어떤 차이가 있을까? 입자간 상호작용이 없는 이상적인 페르미온으로 이루어진 기체를 페르미 기체라고 하는데, 한 개의 입자가 가장 낮은 에너지의 기저 상태를 점거하는 순간, 다른 입자들은 그 외의 에너지 상태를 찾아 들어가야 한다. 따라서 \(N\)개의 입자가 있다면 이들이 모두 동일한 기저 상태에 몰려 들어가는 대신에 [그림 5]와 같이 낮은 에너지 순서로 \(N\)개의 에너지 상태를 차례로 채워나가게 된다. 이때 마지막 \(N\)번째 입자의 에너지를 페르미 에너지(\(E_F\))라고 한다. 이런 상황에서는 보즈-아인슈타인 응축이나 초유체 현상이 도저히 일어날 수 없다. 프릿츠 런던이 헬륨-4의 초유체 상전이 현상이 보즈-아인슈타인 응축이라고 생각했던 이유도 그 당시에는 아직 헬륨-3에서는 비슷한 현상이 발견되지 않았기 때문이다.
고체 속에 존재하는 전자도 페르미온이고 헬륨-3도 페르미온이다. 전자는 원자가 규칙적으로 정렬된 고체라는 구조 속에 존재한다. 헬륨-3 액체에는 그런 결정 구조가 없다. 그럼에도 불구하고 전자와 헬륨-3은 페르미온이라는 공통점을 공유한다. 소련의 탁월한 이론 물리학자 레브 란다우Lev Landau, 1908-1968가 1962년 노벨 물리학상을 받은 이유도 페르미 액체라는 개념을 도입해 액체 헬륨-3과 고체 속 전자의 상태를 통합적으로 이해할 이론적 틀을 제공했다는 것이었다.
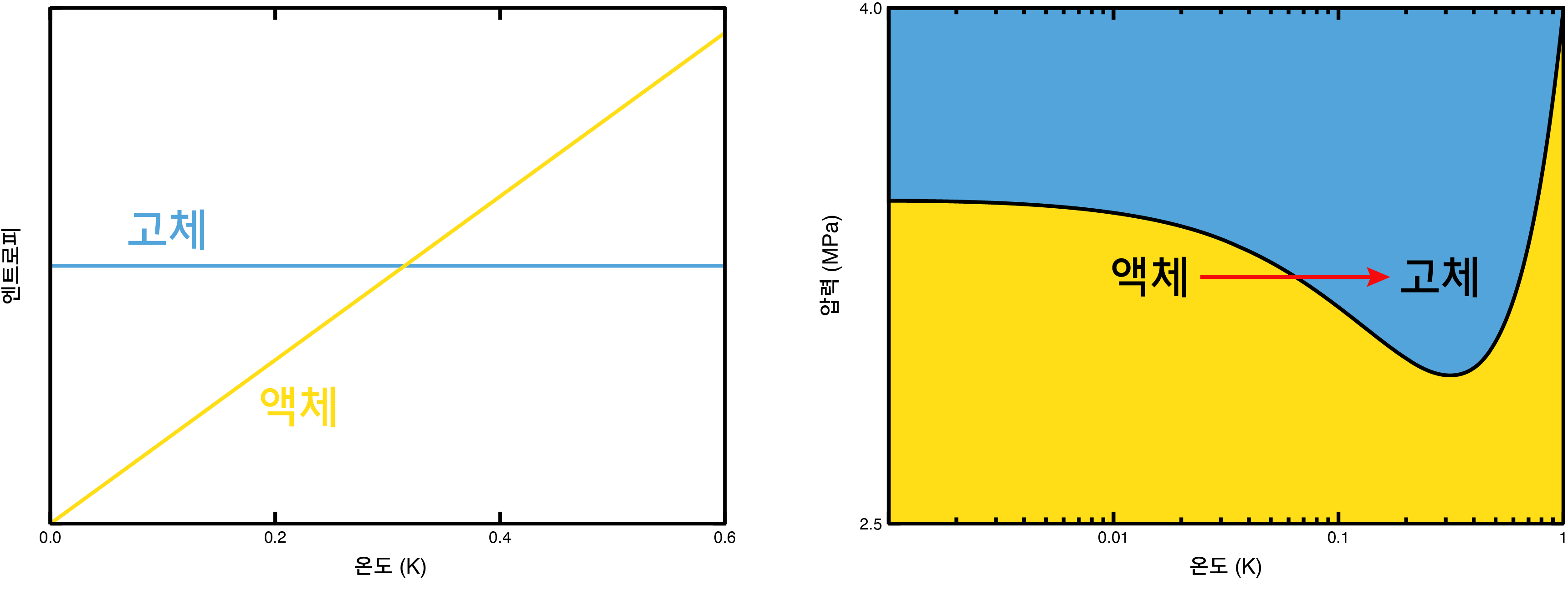
고체 속 전자계의 성질과 액체 헬륨-3의 물리적 성질은 상당히 유사하다. 액체 헬륨-3의 엔트로피는 전자계의 엔트로피와 유사한 방식으로 계산할 수 있고 온도에 비례해서 줄어든다. 헬륨-3 액체에 30기압 이상의 압력을 가하면 고체로 변하는 이유를 이해할 수도 있다. 고체 헬륨-3의 엔트로피를 잘 따져보면 온도에 의존하지 않는 일정한 값을 얻는다. 온도에 따라 증가하는 액체 헬륨-3의 엔트로피와 온도에 무관한 고체 헬륨-3의 엔트로피를 한 그래프에 그려보면 [그림6]처럼 보인다. 충분히 낮은 온도가 되면 액체의 엔트로피가 고체보다 낮아진다. 엔트로피가 물질의 무질서를 나타내는 물리량이라고 한다면, 특정 온도 아래에서는 “고체가 액체보다 무질서해진다!” 고체는 입자들이 정해진 자리에 잘 정렬된 데에 반해서, 액체들은 입자들이 자유롭게 움직일 수 있기 때문에 액체가 고체보다 무질서한 것이 상식이지만, 헬륨-3의 세계에서는 상식적으로 이해할 수 없는 일이 벌어진다는 게 양자역학의 매력이기도 하다.
헬륨-3의 고체-액체 상전이 그림을 살펴보면 절대영도에서는 액체였는데 온도를 올리면서 고체로 바뀌는 온도 구간이 존재한다. 절대영도에서 액체 상태로 존재하는 것만해도 신기한데, 헬륨-3는 온도를 올려서 액체를 고체로 바꿀 수 있는 유일한 물질이기도 하다. 이 신기한 현상은 액체 헬륨-3에서 새로운 물질 상태를 발견하는 수단이 되기도 했다. 대부분의 물질에서 액체-기체 상전이선을 따라 팽창을 통해 기화 냉각을 할 수 있었던 것과 정 반대로 헬륨-3에서는 고체-액체 상전이선을 따라 압축 냉각이 가능하다는 뜻이다. 헬륨-3의 경우 특히 고체-액체 상전이선의 기울기가 매우 완만하기 때문에 비교적 작은 압력을 가해주는 것만으로 크게 온도를 낮출 수 있어서 냉각에 유리하다. 이 방법을 이용하면 0.3K부터 1mK 정도까지 온도를 낮추는 게 가능하다. 액체 헬륨을 2.5mK 이하로 냉각할 수 있었던 덕분에 1971년 액체 헬륨-3의 초유체 상전이가 발견되었다. 여담이지만 올해가 초유체 헬륨-3 발견 50주년이다.
헬륨-4 액체의 초유체 상전이를 보즈-아인슈타인 응축으로 이해할 수 있다고 설명했다. 하지만 보손에서나 가능한 보즈-아인슈타인 응축이 어떻게 페르미온인 헬륨-3에서도 가능한 걸까? 앞서 헬륨-3와 고체 속 전자의 거동이 유사하다고 설명했었는데, 그 유사성은 고체의 전자계가 보여주는 초전도체 상전이와 헬륨-3 액체가 보여주는 상전이 사이에도 계속된다. 두 경우 모두 스핀 \(\frac {-1}{2}\)인 페르미온 입자가 어떻게 상전이를 일으킬 수 있는가하는 문제로 귀결된다.
이런 궁금증을 일시에 해결한 이론이 바딘John Bardeen, 1908-1991-쿠퍼Leon Cooper, 1930-현재-슈리퍼John Schrieffer, 1931-2019가 만든 BCS 초전도 이론이다. 헬륨-4가 보존이라고 하지만, 사실 따지고 보면 헬륨-4 원자 자체는 기본 입자가 아니다. 원자를 구성하는 모든 기본 입자(쿼크와 전자)는 모조리 스핀\(\frac {-1}{2}\)의 페르미온이고, 다만 짝수개의 페르미온 기본 입자가 모여 보손처럼 거동하는 원자를 만들었을 뿐이다. 페르미온을 보손으로 묶어주는 강력이냐, 전자기력이냐는 중요하지 않다. 페르미온인 전자 두 개를 묶어 쿠퍼쌍Cooper pair으로 불리는 전자쌍을 만드는 힘과 헬륨-3 원자 두 개를 묶어 속박된 상태로 만드는 힘은 서로 다르지만 결과적으로 페르미온 두 개를 묶어 보손을 만들어냈다. 그리고 보손은 보스-아인슈타인 응축이라는 상전이를 할 자격을 갖고 있다.
그런 현상이 전도체에서 일어나면 우리는 그것을 초전도체라고 부르고, 헬륨-3 액체에서 일어나는 그것을 초유체라고 부를 뿐이다. 온네스에 의해 페르미온인 전자쌍에 의한 초전도 현상이 초유체 헬륨-4보다 먼저 발견된 것부터가 역설적인 일이지만, 결국 초유체 헬륨-4의 이해를 통해 다시 초전도체를 이해할 수 있는 단초가 제공된 걸 보면, 과학의 발견과 발전은 좀처럼 직선적인 법이 없다는 걸 알 수 있다.
세상에서 가장 순수한 액체
헬륨-3은 금속 초전도체와 마찬가지로 두 개의 헬륨-3 원자가 쿠퍼쌍을 만들어서 발생하는 초유체이지만, 상전이 온도는 초유체 헬륨-4의 상전이 온도나 보통 초전도체의 상전이 온도에 비해 대략 천 배쯤 낮다. 그것 말고도 헬륨-3에 대해 주목할만한 점이 몇 가지 있다. 그중에서 필자의 연구 이력과 밀접한 관계가 있는 헬륨-3의 순도에 대해 이야기를 해보자.
헬륨-3 액체는 10mK 이하의 극저온에서 존재할 수 있는 온 우주에서 가장 순수한 물질이다. 이 세상에서 가장 순수한 금속이 있다면 수은일 것이라고 생각한 온네스의 판단과도 일맥 상통한다. 그 이유는 간단하다. 헬륨-3과 헬륨-4를 제외한 모든 물질은 절대영도에서 고체로 변한다. 헬륨에 불순물이 섞여 있다 하더라도 온도를 충분히 내리면 저절로 고체 덩이로 변해서 헬륨 액체로부터 떨어져 나간다. 헬륨의 정제가 자동으로 되는 셈이다.
10mK 이하의 극저온에서 서로 섞는 게 가능한 액체 물질이 있다면 헬륨-3과 헬륨-4를 서로 섞은 액체가 있을 뿐이다. 실제로 두 물질을 섞을 수도 있지만, 10mK 이하의 온도에서는 액체 헬륨-4에 헬륨-3을 대략 6.6%까지 섞을 수 있을 뿐이다. 그 이상의 헬륨-3를 액체 헬륨-4에 섞으려고 하면, 마치 기름이 물에 뜨듯 액체 헬륨-3가 헬륨-3/헬륨-4 혼합액 위에 둥둥 떠 버린다. 그리고 이렇게 위에 떠 있는 액체 헬륨-3은 불순물이 거의 없어서, 1몰의 액체 헬륨-3에 헬륨-4 원자 1개가 섞여 있을 뿐이다. (이는 현실적으로 측정 가능한 수준의 불순물 농도가 아니고 이론적으로 그럴 것이라고 예측된 값이다.) 역으로 헬륨-3 액체에 헬륨-4를 섞으려고 하면 헬륨-4 액체는 저절로 아래에 가라 앉는다. 헬륨-3은 스스로 불순물을 밀어낸다는 점에서, 많은 물리학 이론이 가정하는 ‘이상적인 상황’에 가장 근접한 물질이다. 이런 이유 때문에 초전도체와 같은 페르미온 양자 액체를 이해하기 위한 이상적인 물질로서 초유체 헬륨-3에 대한 연구도 필요하다.
다른 한 편으로는 세상에 존재하는 (액체 헬륨-3를 제외한) 모든 물질은 불순물을 포함하고 있는 만큼, 액체 헬륨-3에 불순물을 조금이라도 섞을 수 있다면 실재하는 다른 물질에 대한 이해를 도울 수도 있을 것이다. 세상의 모든 고체 물리학자들이 조금 더 깨끗한 시료를 만들기 위한 투쟁을 하는 동안, 액체 헬륨-3 연구자들은 1990년대에 들어서면서 액체 헬륨-3에 불순물을 억지로라도 섞을 방법이 없을까 하는 (얼핏 보기에 배부른) 고민을 하기 시작했다. 그리고 1995년 코넬 대학과 노스웨스턴 대학에서 거의 동시에 에어로젤이라고 하는 다공성 유리를 이용하여 액체 헬륨-3에 적절한 양의 불순물을 주입하는 데 성공한다. ‘더러운 초유체 헬륨-3’을 발견하고, 그에 대한 이론적 해석을 내놓은 공로로 코넬 대학의 지박 파피아Jeevak Parpia, 실험와 필자의 지도 교수인 노스웨스턴 대학의 윌리엄 핼퍼린William Halperin, 실험, 제임스 솔스James Sauls, 이론는 2017년 프릿츠 런던상을 수상하였다.
다들 식품 포장지 안에 들어 있는 실리카젤을 뜯어 본 적이 있을 텐데, 육안으로는 보면 지름 1mm 정도의 투명하고 동그란 구슬 같다. 그렇지만 이를 자세히 들여다보면 직경 수 나노미터 크기의 아주 미세한 구멍들이 송송 뚫려 있는 유리다. 아주 미세한 유리silica알이 서로 뭉쳐서 젤 구조를 형성했다고 해서 실리카젤이라고 한다. 보통의 실리카젤은 전체 부피 중 30% 정도가 유리이고, 약 70%가 비어 있는데, 초유체 헬륨-3에 사용되는 에어로젤이라는 물질은 이보다 밀도가 10배 이상 낮아서, 전체 부피의 1~2% 정도가 유리이고, 98~99% 정도가 비어 있다.
에어로젤에 대해 이야기하자면 이 글을 새로 한 편 쓸 수 있겠지만 (실제로 마크 미오도닉의 책 『사소한 것들의 과학』에서 저자는 에어로젤에 한 단원을 할애하고 있다) 여기서는 그저 약 3~4nm 정도의 작은 유리알이 프랙탈 구조를 이루며 엉겨 붙어서 생성된 물질이라고 해두자. 이 빈 공간에 액체 헬륨-3을 채워 넣으면 3~4nm 크기의 유리알에 헬륨 원자가 충돌하게 되고, 액체 헬륨-3 입장에서는 마치 불순물을 만난 것과 같아진다.
훨씬 흔하디흔한 실리카젤도 같은 이유로 액체 헬륨-3 입장에서 불순물의 역할을 할 수 있는 거 아닌가? 왜 굳이 에어로젤이어야 했을까? 이에 대한 답을 얻기 위해 질문을 조금 바꿔보자. 액체 헬륨-3에 불순물을 섞으면 무슨 일이 벌어질까? 초유체 상전이 온도보다 높은 온도에서는 상당히 많은 양의 불순물을 섞여 있는 헬륨-3이라도 불순물이 없을 때에 비해 별다른 일이 일어나지 않는다. 대부분의 금속은 상당한 양의 불순물을 포함하고 있지만 여전히 드루드 모델이나 페르미 액체 이론과 같은 비교적 단순한 전자 이론으로 그 거동이 설명 가능한 것과 비슷한 맥락이라고 볼 수 있다.
하지만 초유체 상에서는 이야기가 전혀 달라진다. 앞서서 페르미온으로 초유체를 얻기 위해서는 쿠퍼쌍을 만들어야 한다고 했는데, 초유체 헬륨-3의 쿠퍼쌍은 액체 헬륨-3의 원자 간 거리보다 200배에서 1000배 정도 크다. 따라서 불순물이 섞인 상태에서도 이렇게 큰 쿠퍼쌍을 만들 수 있는지 여부가 중요해진다. 불순물 입자들의 평균적인 거리가 쿠퍼쌍의 크기보다 훨씬 크면 불순물의 존재를 거의 무시해도 되겠지만, 불순물이 너무 많아서 불순물 원자 사이의 거리가 쿠퍼쌍의 크기보다 평균적으로 훨씬 짧다면 쿠퍼쌍을 생성할 공간이 충분히 확보되지 않아 초유체 형성 자체가 억제될 수 있다. 불순물의 농도가 쿠퍼쌍의 크기와 비슷해지면 초유체가 생성되긴 하지만 그 특성은 달라질 수 있다.
그리고 전체 부피의 98~99%가 비어 있는 다공성 에어로젤의 경우 유리알들 사이의 빈 공간이 액체 헬륨-3의 쿠퍼쌍 크기와 비슷하거나 그보다 조금 큰 정도라서 초유체 헬륨-3에 새로운 특성들이 나타날 수도 있는 조건을 알맞게 갖추었다. 에어로젤 속에 갇힌 헬륨-3 액체가 보인 첫 번째 특징은 불순물의 농도, 즉 에어로젤의 유리 농도를 높일수록 초유체 상전이 온도가 낮아진다는 점이었다. 불순물이 전혀 없으면 초유체 상전이가 잘 일어나지만 불순물이 너무 많으면 초유체 상전이가 완전히 억제된다는 사실을 생각해 보면, 적당한 양의 불순물이 섞여 있을 때 초유체 상전이 경향이 조금씩 억제될 거라고 예측할 수 있으니, 상당히 자연스러운 결과라고 하겠다.
2001년 필자가 대학원에 진학했을 때 노스웨스턴 대학에서는 이런 ‘더러운 초유체 헬륨-3’의 상전이 그림을 완성하고는 그 외에 불순물의 효과로는 어떤 것들이 있을까에 대한 연구가 한창이었다. 당시 필자가 선택한 연구 주제는 “‘더러운 초유체 헬륨-3’의 비열은 순수한 초유체의 비열과 어떻게 다른가”라는 것이었다. 새로운 물질의 상전이를 발견하면 그 열역학적 특성을 파악하기 위해 비열 측정을 필수적으로 수행하기 마련인데, 1995년에 발견된 ‘더러운 초유체 헬륨-3’의 비열을 6년이 넘도록 아무도 측정하지 않았다는 것이 의외라고 생각할 수도 있다.
상전이 온도가 1mK 근처인 초유체 헬륨-3 실험은 원래부터 실험 사이클이 길고 어렵기로 악명이 높았는데 (당시에 노스웨스턴 대학 물리학과에서는 핼퍼린 교수님 연구실에 들어가서 6년 안에 졸업하지 못하면 10년 후에나 졸업한다는 흉흉한 소문이 있었다), 그중에서도 비열 측정 실험은 난이도가 높은 실험이다 보니 좀처럼 의미 있는 결과가 나오지 않았다. 실제로 필자가 수행한 실험도, 필자가 연구실에 합류하기 전에 이미 졸업한 연구실 선배가 시작했고, 필자의 실험실에서 일했던 박사후 연구원을 거쳐 필자까지 내려온 무려 10년 가까이 3대(?)에 걸쳐 결과를 얻는 대장정이었다.
각고의 고생 끝에 성공한 ‘더러운 초유페 헬륨-3’의 비열 측정을 통해 우리는 무엇을 알아냈을까? 보통의 초전도체나 순수한 초유체 헬륨-3의 비열은 온도가 낮아짐에 따라 지수함수적으로 감소하여 저온에서의 비열이 극도로 작아진다. 이런 관측을 통해 초전도체에서는 페르미 에너지 근처에 입자들이 들어갈 수 있는 에너지 준위들이 없다는 것을 알 수 있는데, 이런 식으로 에너지 준위가 사라져버림으로써 생긴 에너지 간격을 초전도 간극이라고 한다.
대단히 흥미롭게도 ‘더러운 초유체 헬륨-3’는 절대영도 근처에서 일반적인 페르미 액체처럼 비열이 온도에 선형적으로 비례해 감소하는 양상을 띄었다. 이는 헬륨-3 초유체의 페르미 에너지 근방에는 초전도 간극이 존재하지 않는다는 점을 의미했다. 그 당시에는 페르미 에너지 근방에 불순물과 결합한 새로운 에너지 준위들이 생겨났다는 식으로 결론을 내리고 말았는데, 최근에는 이런 페르미 에너지 근방에 형성된 에너지 준위가 마요라나 (준)입자라는 새로운 이름표를 달고 재조명되고 있다. 과감하게 이야기하자면, 비록 그 당시에는 그 의미를 깨닫지 못했지만, 초유체 헬륨-3에서 마요라나 준입자의 흔적을 최초로 발견했다고 이야기할 수 있다.
초전도 간극이 없다는 것과 마요라나 입자가 무슨 상관인지 궁금해하는 이들도 있을 텐데, 이것도 대단히 재미있는 이야기지만, 이는 지난 10년간 응집물질물리 분야에서 가장 주목받고 있는 연구주제 중 하나라는 정도로만 정리해두자. 실제로 필자도 교수로 임용된 후에 연구실 자원의 상당 부분을 초유체 헬륨-3에서 마요라나 준입자를 보다 구체적으로 (재)발견하고 제어하기 위한 실험을 수행하는 데 투입하고 있다. 나름대로는 좋은 아이디어를 갖고 시작한 실험이라고 생각하지만 아직까지는 별다른 결실이 없다. 원대한 포부와 희망을 안고 실험을 시작하지만, 자연이 던지는 난관에 부딪칠 때면 항상 마이크 타이슨의 한 마디를 떠올리게 된다. “누구나 그럴싸한 계획을 갖고 있다. 한대 처맞기 전까지는.” 그렇지만 또 한 편으로는 그렇게 자연에게 얻어맞으면서 새로운 것을 발견해 나가는 것이 과학의 묘미 아니겠는가.
글을 마치며
19세기 중반부터 수많은 과학자들이 지구상의 모든 기체를 액체로 만들기 위한 노력을 기울이기 시작했을 때, 인류는 헬륨의 존재를 알지도 못했다. 1895년 윌리엄 램지가 헬륨을 발견한 이후에 듀어나 온네스 같은 과학자들이 이를 액화하기 위한 노력을 기울이기는 했지만, 사실 헬륨이란 물질이 대단히 심심한 물질이고, 당시에는 인류가 액화하지 못한 마지막 기체 이상의 의미는 없었다. 주기율표의 최상단 최우측에 자리 잡은 헬륨은 우주에서 가장 안정적인 원소로 화학자들이 가장 재미없어하는 물질이다. 그렇지만 화학자들로 하여금 흥미를 잃게 만드는 그런 특성들이 지난 100년 이상의 시간 동안 물리학자들에게는 끊임없이 새로운 발견의 여지를 주었다.
헬륨을 제외하면, 단일 원소의 물질 중에서 이렇게 다양하고 풍부한 물리학적 현상이 발현된 물질은 최근에 엄청나게 각광을 받고 있는 탄소로 된 그래핀 정도만이 있을 뿐이다. 그래핀에 대해서도 우리가 감탄할 이유는 대단히 많지만 (“양자 물질의 역사 [5]: 그래! 핀다!”, “그래핀 무아레 무늬의 마법”, “믿기 힘든 양자 Incredible Quantum [10]: 더 높은 차원으로” 참조), 이 글의 주제는 액체인 만큼 액체 헬륨의 중요성을 새삼 강조해보자면, 그래핀 연구의 상당수도 4K 이하에서 행해지고 있고, 액체 헬륨이 있었기에 가능했다는 사실을 잊지 말자.
액체 헬륨이 물리학 연구에 끼치는 영향력은 그래핀에서 멈추지 않는다. 최근 IBM, 구글 등이 경쟁적으로 달려들고 있는 초전도 소자를 이용한 양자 컴퓨터 연구, 위상 물질을 비롯한 다양한 양자 물질을 발견하기 위한 노력의 배경에는 헬륨을 이용한 저온 냉각 기술이 자리 잡고 있다. 놀라운 사실은 이런 기초 연구를 위한 사용량은 전체 액체 헬륨 사용량의 20% 정도밖에 되지 않는다는 점이다.
액체 헬륨의 가장 큰 소비자들은 놀랍게도 오늘날 우리 삶에 필수적인 의료산업과 반도체 산업이다. 병원에서 진단도구로 사용하는 MRI 기계와 반도체 산업의 핵심인 실리콘 웨이퍼 제작을 위해서는 강하고 안정적인 자기장을 필요로 하는데, 이를 위해 액체 헬륨 온도에서 동작하는 초전도체로 만든 전자석이 사용되기 때문이다. 영하 269도라는 온도는 쉽게 상상도 되지 않는 낮은 온도이지만, 이 낮은 온도와 이 온도에서만 존재하는 엉뚱하다면 엉뚱한 액체가 우리 삶에 이렇게나 가까이 있다. 이 글을 여기까지 읽은 독자라면, 다음에 어디선가 헬륨을 품고 하늘로 떠올라가는 풍선을 보거든, 그렇게 풍선과 함께 하늘로 떠나간 헬륨으로 또 무엇을 할 수 있을까 한 번쯤 공상의 나래를 펼쳐 보면 좋겠다.