우리는 빛과 물질을 통해 자연을 인식합니다. 인류가 자연과학을 발전시킨 역사는 물질을 발견하고, 새로운 물질 현상을 발견하고, 이를 이해하는 과정으로 압축하여 설명할 수 있을 겁니다. 그동안 “물질의 재발견” 연재를 통해 여러 물질의 새로운 면모를 ‘재발견’한 이야기를 나눠 왔습니다.
이번 글에서는 대단히 친숙한 물질 상태인 기체에 관해 살펴보려고 합니다. 기체하면 가장 먼저 떠오르는 것은 공기입니다. 지구는 공기에 둘러싸여 있고, 우리는 태어난 순간부터 지금까지 쉬지 않고 호흡하며 살아왔습니다. 공기는 우리에게 가장 친숙한 물질 상태라고 할 수 있지요. 우리는 경험적으로 공기에 대해 많은 것을 알고 있습니다. 공기는 차가울 수도 따뜻할 수도 있고, 냄새를 품고 색깔을 갖기도 합니다. 공기가 없으면 촛불이 꺼지는데, 이로써 공기 중에 연소에 꼭 필요한 무언가가 있다는 것을 알 수 있습니다. 공기는 소리를 전달하는 데 필요하고, 바람이 되어 위력을 발휘하기도 합니다. 기체는 특정한 부피를 갖는 용기에 담을 수 있고 또한 압력을 행사할 수 있습니다. 풍선, 진공청소기를 살펴보면 이러한 압력의 행사가 아주 가시적으로 나타납니다. 건물 한 채만 한 비행기가 빠른 속도로 공기를 가를 때, 그 육중한 동체가 공기의 도움으로 공중에 뜹니다.
이렇듯 기체는 우리 일상에서 다양하고 중요한 역할을 하지만 동시에 너무나 친숙한 나머지 특별할 것이 없어 보인다는 착각을 주기도 합니다. 물론 진공청소기를 제작하고 비행기 동체를 디자인할 때 공기의 흐름에 대한 정교한 이해가 필요하고, 이런 이해는 비록 더디기는 하지만 지금도 꾸준히 진행 중이라는 점도 인정합니다. 또한, 엄청나게 다양한 기체가 있다는 것도 압니다. 기체를 구성하는 원자나 분자의 종류를 바꾸면 되니까요.
그렇지만 이미 화학자들이 몇 세기에 걸쳐 다양한 기체를 다 분류하고 그 특성을 이해했습니다. 이제 와서 특별히 새로운 성질이 발견될 것 같지는 않습니다. 기체가 재발견되었다고 할 때, 대체 무엇이 새롭게 발견되었다는 것일까요? 기체가 차가워지면 액체나 고체가 될 것이고, 아주 뜨거워지면 기체 분자를 구성하는 전자와 핵이 분리되어 플라즈마가 될 것이라는 예상 정도는 충분히 할 수 있습니다. 그 이상 기체의 숨겨진 면모가 또 무엇이 있을지 궁금할 것입니다.
최근 기체를 액화되지 않은 상태에서 아주 낮은 온도로 냉각하여 독특한 양자 현상을 연구하는 과학자들이 생겼습니다. 물리학에는 이른바 ‘물질파matter wave’라는 개념이 있습니다. 입자들의 집합으로 여겨 왔던 물질이 때로는 파동적인 성질을 보일 때가 있다는 것인데, 이것은 20세기 초 양자역학의 중심 개념으로 받아들여진 후부터 많은 물리 현상을 이해하는 데 길잡이가 되었습니다. 절대 영도에 접근하는 극도로 냉각된 기체는 입자의 집합체라기보다 거대한 물질파의 모습으로 변신합니다. 이러한 기체를 요즘은 ‘양자 기체’라고 부릅니다. 이번 글에서는 아주 차가운 기체, 양자 기체를 소개하려고 합니다. 최근에는 이런 기체 속 원자들을 정교하게 제어하여 다른 새로운 쓸모를 찾으려는 노력도 많이 이루어지고 있답니다.
기체의 고전적 이해
우선 기체에 대한 일반적인 이해를 짧게 정리해 보는 것이 좋겠습니다. 기체 상태는 초중등 과학 교육과정에서 일찌감치 배우는 물질 상태입니다. 그만큼 간단하고 이해하기가 쉽다는 뜻이지요. 기체는 자유롭게 움직입니다. 너무 자유로워서 어느 용기에 담아두어야 하는데, 이 때문에 기체의 부피가 결정됩니다. 기체 상태를 설명하는 다양한 물리량이 있습니다. 바로 밀도, 압력, 온도입니다. 밀도는 부피당 기체의 질량이고, 압력은 기체가 용기를 밀어내는 단위 면적당 힘을 뜻하고, 온도는 기체의 따뜻하고 차가운 정도로 이해할 수 있습니다.
기체의 밀도, 압력, 온도 사이의 관계는 수백 년 전부터 연구됐습니다. 다양한 압력계와 온도계가 제작되었고, 이를 통해 경험 법칙들이 얻어졌지요. 온도가 일정할 때, 부피가 줄어들면 압력이 증가하는 보일의 법칙이 있고, 압력이 일정할 때 기체의 온도를 올리면 부피가 증가하는 샤를의 법칙 등이 있습니다. 이런 물리량들 사이의 관계를 표현한 식을 기체 상태 방정식이라고 합니다.
기체 상태 방정식에 대한 이해는 소위 기체 분자 운동론이 등장하면서 구체화되었습니다. 이 이론에서는 기체가 자유롭게 움직이는 분자들로 구성되어 있다고 보고, 압력은 이러한 구성 분자들이 벽에 부딪히고 튕겨 나오면서 벽에 주는 힘의 합으로 이해합니다. 기체 속 분자 하나하나는 특별한 모양이나 구조가 없고, 분자들끼리는 서로 충돌하는 일도 거의 일어나지 않은 채 존재하는 기체를 이상 기체Ideal gas라고 부르지요. 이상 기체에 대해 이론을 전개하면 이른바 이상 기체 방정식이라는 게 산출되는데, 놀랍게도 대부분의 실재하는 기체의 상태가 이상 기체 방정식을 잘 따릅니다.
기체가 작은 입자들로 이루어졌다는 사실이 처음부터 자명하게 알려진 것은 아니었습니다. 기체의 구성 요소에 대한 본격적인 이해는 19세기 화학의 시작과 함께 형성되었습니다. 아보가드로 법칙, 즉 모든 기체는 같은 온도, 같은 압력에서 같은 부피 속에 같은 개수의 입자를 포함한다는 것이 밝혀지면서 기체가 작은 분자들로 구성되어 있다는 게 명확해졌습니다. 물질이 원자들로 구성되어 있다는 사실을 알아낸 것은 인류가 자연을 탐구하면서 이뤄낸 엄청난 산출물입니다. 물질을 구성하는 입자들의 종류와 이들이 모여 조직되는 방식, 또 입자들 사이의 상호작용에 따라 다양한 모습으로 그 상태를 드러내는 게 바로 물질이지요. 유명한 물리학자 리차드 파인만은 이러한 원자 개념의 중요성을 다음과 같이 표현한 바 있습니다.
“모든 과학 지식이 다 사라진다 해도 물질이 원자로 구성되어있다는 사실만은 전수되어야 한다는 이야기인데, 설득력이 있습니다. 물론 계속되는 탐구를 통해 원자 자체가 무엇으로, 어떻게 구성되었는지 살펴보는 것도 매우 중요한 일입니다. 하지만 거시적인 세계에 존재하는 물질의 성질을 이해하려고 할 때는 원자 자체를 실질적인 중심 개념으로, 출발점으로 삼아도 괜찮습니다. 우주의 탄생 과정이나 입자 가속기 속에서 입자가 충돌하고 생성되는 과정이 아니라 우리가 흔히 인지할 수 있는 수준의 현상을 이해하고자 할 때는 그렇습니다.”
“If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis (or the atomic fact, or whatever you wish to call it) that all things are made of atoms—little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied. (The Feynman Lectures on Physics, Vol. I, chapter 1)”
기체 분자 운동론은 이상 기체 방정식을 제시함으로써 기체의 부피와 압력, 온도 사이에 존재하는 실험적 관측 사실을 잘 설명한다는 점에서 대단히 성공한 이론입니다. 그러면서 동시에 이를 넘어서는 특별한 물리학적 의미도 지닙니다. 다름이 아니라 수많은 입자로 구성된 거시적인 물리계의 성질을 구성 입자들의 미시적인 움직임과 연결하는 데 성공했다는 점입니다.
이전까지의 물리학은 한 입자의 움직임만을 기술하고 살피는 것이 주 임무였다면 기체 분자 운동랑이 나오면서부터는 많은 수의 입자들로 구성된 물리계의 성질도 체계적으로 이야기할 수 있게 된 것입니다. 다수의 입자로 구성된 물질의 거동을 다루는 역학을 뉴턴 역학과 구분 지어 통계 역학이라고 부릅니다. 뉴턴 역학이 단일 물체의 동역학을 집중적으로 다루었다면, 통계 역학은 많은 수의 구성원으로 이루어진 다체계 물질을 구성하는 개별 입자의 동역학을 바탕으로 전체 계의 성질을 밝혀내고자 합니다. 기체 분자 운동론은 통계 역학의 시작점이었다고 할 수 있습니다.
그저 따뜻하고 차가운 정도를 표현하는 것으로 이해했던 온도라는 개념에 대한 물리학적 이해도 기체 분자 운동론을 통해 확실해졌습니다. 온도라는 것은 본래 매우 주관적이고 직관적인 개념이었습니다. 한 손은 차가운 물에, 다른 손은 뜨거운 물에 넣었다가 두 손을 모두 미지근한 물에 담그면 차가운 물에 있었던 손은 따뜻하게, 뜨거운 물에 넣었던 손은 시원하게 느낍니다. 기체 분자 운동 이론에 따르면 온도는 분자들의 평균 운동 에너지와 연관되어 있습니다. 좀 더 정확히 말하면 온도는 기체 속 분자들이 갖는 운동 에너지의 평균값, 그 자체라는 겁니다. 온도의 물리학적 의미가 드디어 드러나게 된 것입니다. 켈빈Kelvin, K이라는 온도 단위를 사용하면 (섭씨 영도는 273.15K에 해당함) 분자의 운동 에너지가 온도에 정비례한다는 걸 증명할 수 있습니다. 방 안 공기가 섭씨 20도라고 할 때, 공기에 포함된 질소 분자들의 평균 속력은 대략 500m/s 정도 됩니다. 지금도 분자들은 이렇게 엄청난 속도로 움직이며 서로 충돌하고 있습니다.
물론 분자가 움직이는 평균적인 빠르기가 수백 m/s 라는 것일 뿐이고, 개별 분자는 제각각의 속도로 움직입니다. 이런 상황에서 궁금한 건 분자의 운동 속도 분포라는 양입니다. 어떤 분자는 평균 속력보다 빠르게, 어떤 분자는 그보다 느리게 움직일 텐데, 그 비율이 각각 어떻게 주어지는지를 결정하는 분포 함수가 궁금하다는 의미지요. 분자 사이에 전혀 상호작용이 없다면 분자의 운동 속도 분포는 애초에 기체가 만들어질 때의 값 그대로 유지될 겁니다. 설령 기체가 벽에 부딪히더라도 운동하는 방향만 바뀔 뿐 빠르기는 달라지지 않습니다. 실제 분자들은 아주 작지만 유한한 크기를 갖고 있고, 짧은 시간 동안이나마 서로 만나고 충돌하면서 에너지를 교환합니다. 너무 빠른 분자들은 조금 느려지고, 너무 느리게 움직이던 분자는 충돌을 통해 에너지를 얻어 조금 빨라집니다.
충분히 많은 시간이 지난 후에, 그러니까 이런 분자 사이의 충돌이 충분히 많이 일어난 후에 분자들이 보여주는 속도 분포는 어떻게 될까요? 이 흥미로운 문제에 대한 답은 19세기의 탁월한 물리학자 맥스웰이 처음 제안했고, 이후 또 다른 시대의 물리학자 볼츠만이 이런 속도 분포가 형성되는 과정에 대해 더 상세히 설명했습니다. 이렇게 해서 얻어진 결과를 맥스웰-볼츠만 분포라고 부릅니다. 좀 전문적으로 이야기하자면 맥스웰-볼츠만 분포는, 분자의 총 에너지가 일정한 값으로 고정되었다고 가정한 상황에서 기체가 갖는 엔트로피가 최대가 되게끔 해주는 분포라고 생각할 수 있습니다. 좀 더 간단히 이야기하면 총 에너지가 주어진 상황에서 기체에 허용되는 물리적으로 가장 복잡한 상태라고 할 수 있습니다. 맥스웰-볼츠만 속도 분포는 기체 속에서 분자가 확산하거나 열을 전달하는 과정 등을 이해하는 길을 열어 줍니다. 예를 들어 어떤 냄새는 다른 냄새보다 빠르게 퍼지는데, 왜일까요? 각 냄새에 해당하는 분자의 질량이 서로 다르기 때문에 각 분자가 움직이는 평균 속도가 달라지기 때문입니다.
온도가 기체를 구성하는 분자 움직임의 평균 속도와 관련된다고 한다면, 자연스럽게 모든 입자가 정지한 가장 조용한 상태도 상상해 볼 수 있습니다. 이런 상태의 온도를 절대 영도라고 합니다. 이미 샤를의 법칙에서 기체의 부피가 0이 되는 온도로서 절대 영도가 한 번 등장했던 적이 있습니다. 기체의 부피가 음수 값을 갖지는 못할 테니까요. 입자의 움직임이 가장 적어진 상태, 궁극의 바닥 상태, 이것이 절대 영도입니다.
절대 영도에 도달한 기체를 만들 수 있을까요? 언뜻 생각하면 불가능해 보입니다. 기체의 온도가 줄어들면 부피도 함께 줄어들어 기체를 구성하는 입자의 밀도가 올라갑니다. 그럼 입자들끼리 충돌하는 사건도 점점 더 자주 발생합니다. 점차 입자들 사이의 상호작용 효과가 중요해진다는 뜻이지요. 이런 문제를 해결하는 데 뛰어난 업적을 남긴 과학자가 판데르발스입니다. 그는 분자에 유한한 부피가 있다는 점, 그리고 분자 사이에는 서로 당기는 힘도 작용하기 때문에 압력이 변할 수 있다는 점 등을 고려해서 이상 기체 방정식을 변형한 새로운 기체 상태 방정식을 제안했습니다.
이를 통해 기체가 액체로 변하는 상전이 현상을 자세히 연구할 수 있었고, 상전이 과정에서 발생하는 잠열이란 것도 설명할 수 있었습니다. 기체가 액화할 때 발생하는 잠열에 대한 이해를 통해 비로소 냉장 기술의 발전이 가능했습니다. 판데르발스는 이런 업적 덕분에 1910년 노벨 물리학상을 받았지요. 냉장 기술의 발전은 액체 헬륨을 실험실에서 얻을 수 있는 길을 열어 주었는데, 궁금한 독자는 “액체의 재발견[1]: 액화의 역사”, “액체의 재발견[2]: 영원히 얼지 않는 액체 헬륨 이야기”를 살펴보기 바랍니다. 흥미진진한 액화 실험의 역사가 잘 서술되어 있습니다.
절대 영도의 기체, 과연 불가능할까요? 이미 몇십 년 전부터 아주 낮은 밀도의 기체가 액체로 변하지 않고 준안정적인 상태를 유지하면서 절대 영도에서 불과 수십 나노 켈빈 정도 떨어진 아주 낮은 온도로 냉각되는 일이 실험실에서 구현되고 있습니다. 이런 극저온 기체를 만들려면 레이저 냉각법이라고 불리는 기술을 사용해야 합니다. 먼저 그 작동 원리를 살펴보도록 하지요.
원자 기체의 레이저 냉각
원자는 전자와 핵으로 구성되어 있는데, 전자와 핵은 서로 반대 전하를 갖고 전자기력으로 묶여 있습니다. 빛은 전기장과 자기장의 교차 유도 현상이고, 전하는 빛을 흡수하거나 방출할 수 있습니다. 전하로 구성된 원자도 빛을 흡수하고 방출합니다. 빛을 흡수하거나 방출할 때마다 원자는 에너지를 얻거나 잃습니다. 이런 에너지 변화는 원자의 내부 상태 변화를 동시에 가져옵니다. 달리 말하면 원자에 흡수 또는 방출되는 빛의 에너지 분포, 즉 색깔 분포를 잘 들여다보면 원자의 내부 상태를 간접적으로 들여다볼 수 있다는 의미입니다.
현대 물리학에서는 이러한 연구를 분광학이라고 합니다. 수소는 양성자 하나와 전자 하나로 구성된 가장 간단한 원자입니다. 수소 원자의 분광 구조를 관측하고 설명하는 과정에서 20세기 초 양자역학이 태동했고, 물질에 대한 양자역학적 이해의 틀이 정립되었습니다. 전하를 갖는 입자와 빛의 상호작용을 다루는 양자전기역학은 역사상 가장 성공한 이론으로 손꼽히고 있습니다. 전자의 스핀 자기 모멘트를 0.00000001% 수준에서 정확히 예측하였고, 이것이 실험으로 측정되었기 때문입니다. 이론도 이론이지만 이 정도의 정밀도로 측정하는 실험도 놀랍습니다.
원자에 관한 분광학 연구가 계속되면서 차츰 물리학자들은 원자의 내부 상태를 좀 더 자세히 연구하기 위해 빛을 이용해 원자를 제어하는 방법을 생각하게 됩니다. 원자의 운동이 맥스웰-볼츠만 속도 분포를 갖고 있듯, 원자의 내부 상태도 어떤 분포를 따릅니다. 같은 기체 속에 있더라도 어떤 원자의 내부 상태는 A, 다른 원자의 내부 상태는 B, 이렇게 주어진다는 뜻이지요. 이 때문에 원자 기체에서 나오는 분광 신호도 다양한 내부 상태에 대한 신호의 합으로 주어집니다. 상태 분포가 복잡하면 신호도 복잡해지고, 명확한 분석이 어려워집니다.
만일 빛을 이용하여 특정한 내부 상태로 모든 원자를 정렬할 수 있다면 분광학 관점에서 대단히 유용할 겁니다. 이런 기술을 광학 펌핑optical pumping이라고 부르는데, 이런 기술 덕분에 원자의 내부 구조를 더 정확히 연구할 수 있게 됐습니다. 더불어 원자를 특정한 내부 상태로 다 정렬시킨 경우, 수많은 원자가 동일한 빛을 낼 텐데, 이런 원리를 바탕으로 만들어진 게 우리가 익히 들어왔고 생활과 산업 곳곳에서 다양하게 사용되는 레이저입니다. 레이저 개발 이야기는 아주 흥미진진하지만 여기서는 더 깊이 들어가지 않겠습니다. 현대 물리학에서 빛의 재발견이라고 하면 레이저의 이해와 개발이 아닐까 싶네요. 광학 펌핑 기술을 개발한 알프레드 카스틀러Alfred Kastler는 1966년 노벨 물리학상을 받았습니다.
레이저의 개발 덕분에 분광학 연구의 정밀도는 점점 더 높아졌고, 이제는 원자의 운동이 분광 신호에 미치는 영향까지 측정하는 수준에 이르게 됩니다. 소방차가 우리를 향해 올 때와 우리에게서 멀어질 때 내는 소리의 높이가 다르다는 걸 잘 알고 있을 겁니다. 이를 도플러 효과라고 하는데 원자에서 나오는 빛도 원자가 어느 속도로 움직이는지에 따라 우리가 볼 때 그 색깔이 달리 보인다는 것입니다. 이는 원자의 내부 상태, 다른 말로 하면 에너지 준위를 더욱 정확하게 알고 싶은 물리학자의 끝없는 바람에 장벽이 되지요. 대략 수백 m/s로 움직이는 원자가 가시광 대역의 빛을 방출할 때, 원자의 움직임으로 인해 GHz (109Hz) 정도의 주파수 변화가 발생합니다.
어떤 물질 속 원자는 주어진 온도에 비례하는 운동 에너지를 갖습니다. 원자가 계속 움직인다는 뜻이지요. 이걸 한 마디로 열적 요동이라고 합니다. 그리고 열적 요동으로 인해 분광 신호가 넓어지는 현상을 도플러 퍼짐Doppler broadening이라고 하지요. 분광학 연구가 발전하면서 도플러 퍼짐을 교묘하게 피하는 다양한 방법들이 등장했지만, 이제는 이걸 넘어서는 뭔가 새로운 걸 해 보고 싶다는 생각이 물리학자들 마음속에 생겼습니다. 그동안은 원자의 내부 상태를 잘 제어해 봤으니, 이제는 원자의 외부 움직임까지 제어할 수는 없을까? 물리학자들의 호기심과 자연을 제어하고픈 욕구는 정말 멈출 줄 모릅니다.
원자는 빛을 흡수하고 방출하면서 에너지를 얻고 잃을 뿐만 아니라 빛으로부터 힘도 받습니다. 순수한 전자기장 파동으로 여겨지던 빛이 알고 보니 에너지와 운동량을 지닌 빛 알갱이(광자photon)였다는 깨달음이 20세기 초 양자역학의 서막이었습니다. 광자라는 개념은 물체에서 나오는 빛의 색깔 분포를 이해하려는 방안으로 막스 플랑크가 처음 어렴풋이 제안했고, 이후에는 물체에 빛을 쏘여주면 특정 주파수 이상에서만 전자가 튀어나오는 광전 효과, 전하를 띤 입자와 빛이 산란을 일으키는 콤프턴 산란 등의 관측을 통해 극명하게 확인되었습니다.
만일 원자에 움직이는 방향과 반대로 진행하는 레이저 빔을 쏘아주고 원자로 계속해서 이 빛을 흡수하고 방출하도록 한다면 어떤 일이 벌어질까요? 광자를 흡수할 때마다 (운동 반대 방향으로 힘을 받은) 원자의 속도는 조금씩 느려지게 될 것이고 결국 완전히 운동이 멈출 수도 있을 겁니다. 마치 날아가는 야구공에 수만 개의 탁구공을 반대 방향으로 충돌 시켜 야구공의 움직임이 느려지도록 하는 것과 비슷합니다. 원자가 광자를 흡수하고 방출하는 데 걸리는 시간은 대략 수백 나노nano(10-9)초로 아주 짧으니, 비록 광자의 운동량이 지극히 적다 하더라도 빠른 시간 안에 원자를 감속시킬 수 있을 겁니다.
이제 원자의 운동을 전후좌우, 그리고 위아래 모든 방향으로 느리게 하는 방법을 생각해 보지요. 원자에게 전후좌우 아래위, 이렇게 여섯 개의 방향에서 레이저 빔을 쏴 주고, 게다가 레이저 빔의 색깔을 원자가 좋아하는, 즉 잘 흡수하는 색깔에 비해 약간 더 빨간 쪽(주파수가 낮은 쪽)으로 맞췄다고 합시다. 이런 상황에서 원자는 여섯 개의 레이저 중 어느 쪽의 광자를 더 잘 흡수할까요?
도플러 효과를 생각하면 답이 간단히 나옵니다. 원자는 자신의 움직이는 방향과 반대쪽으로 진행하는 레이저 빔을 다른 다섯 개의 레이저 빔에 비해 약간 파란 색으로, 즉 주파수가 더 높은 쪽으로 봅니다. 본래 레이저의 주파수가 원자가 흡수하기에 딱 좋은 값보다 살짝 작았으니까, 도플러 효과까지 고려하면 이제 흡수하기 딱 좋은 주파수의 레이저 빛이 되는 셈이지요. 따라서 원자가 움직이는 방향과 반대 쪽으로 진행하는 레이저로부터 광자를 흡수할 확률이 더 높고, 따라서 원자는 감속할 겁니다. 원자가 어느 방향으로 움직이든 마찬가지 이유로 움직이는 속도와 반대 방향의 힘, 즉 마찰력과 비슷한 힘을 느끼게 될 테니 이는 원자의 속도가 점차 줄어든다는 의미입니다.
광자의 선택적 흡수를 유발하여 원자의 속도를 줄이는 기술을 레이저 냉각 기술이라고 합니다. 최적화된 조건에서 원자의 속도는 수 cm/s까지 줄어들 수 있는데, 이를 온도로 환산하면 대략 수백 마이크로micro(10-6)켈빈에 해당합니다. 수백 켈빈의 원자 기체 시료가 수백 마이크로 켈빈으로 냉각된 것이지요. 기왕에 절대 영도까지 냉각할 수는 없을까요? 냉각 한계는 광자 하나가 갖는 운동량에 기인합니다. 정지한 원자가 광자 하나와 충돌을 한 후 얻는 운동 에너지가 대략 마이크로 켈빈에 해당합니다. 즉 마이크로 켈빈 정도가 되면 원자는 광자의 충돌 효과를 아주 거칠게 느끼게 되고 더 조용해질 수가 없는 것이지요.
여기서 중요한 질문이 있습니다. 왜 기체가 수백 마이크로 켈빈까지 냉각되었는데, 액체 혹은 고체로 변하지 않는 걸까요? 이렇게 낮은 온도에 존재하는 원자들이라면 당연히 고체 상태를 이루는 게 안정적입니다. 수증기를 유리 상자 안에 담고 냉각시키면 어느 온도부터 상자의 한쪽 구석에서 응결이 일어나고, 더 낮은 온도에서는 얼음이 만들어지는 게 자연스럽습니다. 그런데 또 생각해 보면 응결이 일어나려면 원자가 조밀하게 한 곳에 모여야 하고, 그러기 위해서는 적어도 세 개의 원자가 동시에 충돌하는 사건이 자주 일어나야만 합니다.
왜냐하면, 두 개의 원자만 충돌할 경우 에너지 보존 법칙에 따라 두 원자는 서로 붙어 분자를 만들기 어렵고, 단순히 운동량과 에너지만을 교환한 뒤 다시 멀어지게 되기 때문이지요. 반면 세 개의 원자가 동시에 충돌하는 경우에는 충돌 직후 두 개의 원자는 서로 달라붙고 나머지 한 개의 원자가 잉여의 운동 에너지를 모두 갖고 달아나는 것이 가능해집니다. 응결이 진행될 수 있는 것이지요. 일단 이런 응결 씨앗이 한 번 만들어지면 다른 원자들이 와서 달라붙는 게 더 쉬워집니다.
레이저 냉각으로 준비된 저온 원자 기체는 그 밀도가 대략 1010~1013cm-3 로 방 안 공기의 밀도보다 약 1000만 배 이상 낮습니다. 아주 희박한 기체입니다. 이 때문에 고체가 되기 위해 필요한 세 원자 충돌 사건이 매우 드물게 일어나고, 원자들은 수백 마이크로 켈빈의 온도에서 기체 상태를 계속 준안정적으로 유지하게 됩니다. 물론 이러한 저온 원자 기체 실험은 고진공이란 환경을 인공적으로 만들어 준 실험 챔버chamber 안에서 진행되고, 기체 시료는 상온의 다른 물체와 물리적인 접촉을 전혀 하지 않으면서 생성됩니다.
보스-아인슈타인 응축
기체 냉각을 이보다 한층 더 진행해 볼 수는 없을까요? “액체의 재발견[2]: 영원히 얼지 않는 액체 헬륨 이야기”에서 살펴본 것처럼 기체를 계속 낮은 온도로 냉각하다 보면 뭔가 새롭고 극적인 일이 벌어질 것만 같습니다. 이 기대에 부응하는 현상이 바로 보스-아인슈타인 응축Bose-Einstein condensation입니다.
자연계의 모든 입자는 스핀spin(입자의 고유한 양자적 특성)의 크기에 따라 두 종류, 즉 보손과 페르미온으로 구별됩니다. 정수의 스핀 값을 갖는 입자를 보손, 반정수의 스핀 값을 갖는 입자를 페르미온이라고 하는데, 페르미온은 파울리 배타원리의 지배를 받아 동일한 에너지 상태에 두 개 이상의 동일한 입자가 존재할 수 없는 반면, 보손은 동일한 에너지 상태에 여러 동일한 입자가 함께 존재할 수 있는 큰 차이가 있습니다. 왜 꼭 이렇게 되어야 하는지 묻는다면 입자의 스핀과 관련한 비밀스러운 설명이 있지만, 꽤 복잡합니다. 자연이 정한 원칙으로 받아들이도록 하지요.
동일한 입자는 서로 구별할 수 없다는 원칙도 있습니다. 가령 전자 열 개가 있으면 그중에 어떤 전자를 다른 전자로 맞바꾸어도 전혀 티가 나지 않습니다. 보손도 마찬가지입니다. 이런 이유로 보손의 경우에는 흥미로운 경우의 수 문제가 발생합니다. 예를 들어 살펴봅시다. 스키장에 슬로프가 3개 있고 3명의 보더가 슬로프를 타고 있다고 합시다. 이 보더들이 모두 같은 슬로프에 있을 확률은 어떻게 될까요? 일반적으로 따져보면 이렇습니다. 보더들이 세 개의 슬로프에 분포하는 모든 경우의 수는 3x3x3으로 27가지입니다. 이 중 모든 보더가 같은 슬로프에 있는 경우는 3가지이니, 확률로 따지면 \( \frac{1}{9}\)가 되겠지요.
자, 이제 보더들을 인간이 아닌 보손들로 대치하겠습니다. 자연이 부여한 원칙에 따라 보더들은 서로 구별이 안 됩니다. 이런 경우, 확률을 따지는 방법이 바뀝니다. 가능한 경우의 수가 27가지 대신 10가지로 바뀝니다. 한 슬로프에 3명 모두가 있는 경우가 3가지, 한 슬로프에 2명 다른 슬로프에 1명이 있는 경우가 6가지, 그리고 각 슬로프에 1명씩 있는 경우가 1가지, 이렇게 총 10가지 경우만 있습니다. 이 중에서 한 슬로프에 모든 보더가 있는 경우는 3가지이니 확률로 보면 \(\frac{3}{10}\)이 됩니다. 이전 경우, 즉 보더가 서로 구분 가능하다고 했을 때와 비교하면 확률이 무려 3배 정도 증가했습니다. 놀랍지 않습니까? 보더를 구분할 수 있는지 없는지에 따라서 확률 분포가 크게 바뀐다는 것이고, 이를 용감하게 일반화하면 보손은 구별 가능한 고전적인 입자에 비해 한 곳에 함께 모이려는 경향이 강하다고 주장할 수 있겠네요. 파울리의 배타 원리는 페르미온들이 한 곳에 함께 있을 수가 없다는 것을 이야기하는데, 보손의 경우는 이와 완전히 반대이지요. 만일 보더들이 보손이라는 것을 안다면 사고 위험이 더 크니 보험율을 좀 더 높게 책정해야 하겠습니다.
조금 더 수학적인 경우를 살펴보지요. \(N\)개의 입자가 2개의 서로 다른 에너지 준위, \(a\)와 \(b\)에 분포하는 경우입니다. \(a\)와 \(b\)의 에너지가 같다면 입자의 양쪽에 모두 골고루 분포할 겁니다. 즉, 각 에너지 준위에 입자가 있을 확률이 \(\frac{1}{2}\)씩이라는 거지요. 그런데 만약 \(a\)의 에너지 값이 \(b\)보다 높다고 해봅시다. 그럼 아무래도 입자가 \(a\)상태에 있을 확률이 좀 더 낮을 겁니다. 즉, 어떤 입자가 \(a\)에 있을 확률은 \(\frac{p}{(1+p)}\)이고 \(b\)에 있을 확률은 \(\frac{1}{(1+p)}\), 이렇게 생각할 수 있습니다. 여기서 \(p\)는 0과 1 사이의 어떤 숫자라고 생각하면 됩니다. 높은 에너지 상태 \(a\)에 입자가 있을 확률이 \(b\)에 비해 \(p\)만큼 줄어든 셈이지요. 이제 \(N\)개의 입자가 동일한 경향성을 가진 채 분포하고 있다고 합시다. 만일 \(N\)개의 입자가 구별 가능하다면 총 \(2^N\)개의 서로 다른 방식으로 입자를 배치할 수 있습니다. 그리고 모든 입자가 독립적으로 자신이 들어갈 상태를 선택한다고 치면 에너지 준위 \(a\)에 들어 있는 평균 입자 개수는 \(\frac{NP}{(1+p)}\)가 될 겁니다.
이제 입자가 서로 구별되지 않는 경우를 살펴보지요. 가능한 입자 배치 경우의 수가 고작 \(N+1\)개로 줄어듭니다. 어느 입자가 어디에 있는지가 중요하지 않고, 각 에너지 준위에 몇 개의 입자가 있는지만 중요하기 때문에 \(N+1\)개의 경우가 나옵니다. 즉 \(a\)에 입자가 \(0,1,…,N\)개 있는 경우입니다. 이번에는 \(a\)에 들어 있는 입자의 평균 개수를 계산해 보겠습니다. 조금 복잡하기는 하지만 고등학교 수학 실력만으로 충분히 알아낼 수 있습니다. 답은 \(\frac{p}{1-p}-(N+1)\frac{p^{N+1}}{1-p^{N+1}} \)입니다. 구분 가능한 입자를 가정했던 앞의 경우와 많이 다르지요. 총 입자 개수 \(N\)이 무한대로 커지는 경우를 따져보면 그 차이가 극적으로 드러납니다. 입자를 구별할 수 있는 경우에는 높은 에너지 상태 \(a\)에 들어 있는 평균 입자의 개수도 함께 무한대로 커집니다. 반면 입자를 구별할 수 없는 경우에는 이게 딱 \(\frac{p}{(1-p)}\)로 제한됩니다. 높은 에너지 상태에 들어갈 수 있는 입자의 개수가 제한된다는 뜻입니다.
아인슈타인이 1920년대 후반에 이론적으로 관측한 사실이 정확히 이런 것이었습니다. 입자의 구별 불가능성을 고려하면 우리가 일반적으로 기대했던 것과는 달리 (에너지가 높은) 들뜸 상태에 존재하는 입자의 개수는 제한된다는 것, 즉 들뜸 상태의 포화가 이루어진다는 것, 그리고 그 밖의 잉여 입자들은 모두 (에너지가 낮은) 바닥 상태에 들어차게 된다는 것입니다. 이것이 보스-아인슈타인 응축 현상입니다. 이것은 보손들이 잔뜩 모여있는 물리계에서 입자의 밀도가 충분히 커지거나 온도가 충분히 낮아질 때 발생합니다. 이런 응축이 일단 일어나면 이 물리계는 거대한 수의 입자가 들어찬 바닥 상태와 포화된 들뜸 상태의 합으로 볼 수 있습니다. 동일한 바닥 상태를 공유하는 입자들의 집합을 특별히 보스-아인슈타인 응집체Bose-Einstein condensate, BEC라고 지칭합니다.
아인슈타인이 이런 이론적 예측에 도달했던 과정도 흥미롭습니다. 우선 보스-아인슈타인 응축이라는 이름에서 알 수 있듯이 보스Satyendra N. Bose가 이 이론의 시작을 가져왔습니다. 1924년, 보스는 흑체 복사를 설명하기 위한 새로운 시도로 광자들을 서로 구별할 수 없는 입자로 취급하고는 앞서 소개한 경우의 수 문제 풀이와 비슷한 방식으로 광자 분포에 대한 경우의 수를 잘 따져서 흑체복사 스펙트럼을 설명하는 이론을 만듭니다. 보스는 이 결과를 정리한 논문을 이런저런 학술지에 보냈지만 모두 게재를 거부당했습니다. 보스는 대신 편지를 써서 자신의 논문을 아인슈타인에게 소개합니다.
아인슈타인은 보스의 이론이 갖고 있던 새로움을 바로 인식했고 그의 논문을 독일어로 직접 번역해 논문이 독일 학술지에 출판될 수 있게 추천하고 도와줍니다. 그런데 여기서 아인슈타인은 한발 더 나아가 질량이 있는 입자에 동일한 논리를 적용해 봅니다. 광자는 질량이 없는 입자고, 질량이 있는 입자는 이에 비해 운동량과 에너지 사이의 관계가 달라집니다. 질량이 유한한 보손 입자들이 모인 집단에서는 어떤 임계 밀도 이상이 되는 순간 보스-아인슈타인 응축 현상이 일어난다는 예측은 이렇게 만들어졌습니다. 질량이 0인 광자의 집단에서는 보스-아인슈타인 응축이 일어나지 않습니다.
정말로 ‘아인슈타인다운’ 생각의 전개가 아닐 수 없습니다. 이 당시 아인슈타인은 드브로이가 발표한 물질파 논문에 대해 알고 이해하고 있었다고 합니다. 물질파 이론이라는 건 우리가 입자라고 생각하던 것들을 파동으로 생각할 수도 있고, 입자의 속성인 운동량이나 에너지를 파동의 속성이라고 할 파장이나 주파수로 해석할 수도 있다는 주장입니다. 보스는 자신의 논문에서 파동으로 흔히 여기던 빛을 구별 불가능한 입자들로 보고 이론을 만들었지요. 아인슈타인은 드브로이의 이론을 본받아, 흔히 입자라고 생각하던 물질계를 물질파, 즉 일종의 파동계로 바라보는 시도를 했다고 생각해 볼 수 있습니다.
보스-아인슈타인 응축이 발생하는 임계 조건을 잘 따져보면, 어떤 입자가 갖는 물질파 파장의 크기가 입자 간 평균 간격과 비슷해지는 바로 그 시점에 보스-아인슈타인 응축 현상이 나타납니다. 온도가 낮아지면 입자의 드브로이 물질파의 크기는 (온도의 제곱근에 반비례해서) 차츰 커지고, 이 커진 물질파가 주변의 다른 입자들의 물질파와 겹치기 시작하는 순간, 바로 그 순간 보스-아인슈타인 응축 현상이 발생한다고 생각할 수 있습니다. 양자역학의 파동 방정식을 주창한 업적으로 유명한 슈뢰딩거도 아인슈타인의 이 연구 결과를 통해 드브로이의 물질파 이론을 처음 접하게 되었다고 합니다. 물리학의 역사에서 1920년대는 참으로 역동적인 시기였던 것이 분명합니다.
바닥 상태에 응축된 보손 입자들은 단순히 같은 양자 상태에 함께 있을 뿐만 아니라 외부 자극에 대해서 집단적인 반응을 보이는 경향이 있습니다. 이런 집단 반응하는 능력이 저온 액체 헬륨이나 초전도체에서 관측된 초유체성superfluidity의 바탕 원리로 작용합니다. 초유체성과 보스-아인슈타인 응축 사이의 관계는 오랜 기간 해결되지 않은 문제로 여겨졌습니다. 1930년대에 액체 헬륨이 보이는 초유체 상에 대한 초기 연구에서 액체 헬륨이 마치 두 개의 유체가 혼합된 유체처럼 행동한다는 사실이 밝혀졌습니다. 마찰이 있는 보통의 유체와 엔트로피가 없고 마찰도 없이 흐르는 유체가 섞여 있는 형태로 액체 헬륨을 이해할 수 있었다는 뜻이지요.
이런 관측으로부터 헬륨 초유체의 본질이 보스-아인슈타인 응축 상태일 것이라는 제안이 나왔고, 이후로 많은 물리학자 사이에 갑론을박이 이어졌습니다. 아인슈타인 본인도 이러한 논의를 접한 후에 본인이 한 예측의 중요성을 진지하게 다시 생각하기 시작했다고 합니다. 아쉽게도 액체 헬륨의 경우는 헬륨 원자들 사이의 상호작용이 너무 강하기 때문에 초유체성과 보스-아인슈타인 응축 사이의 관계를 명확하게 확인하는 게 불가능했습니다. 그래서 물리학자들은 헬륨 액체가 아니라 이상 기체 상태에서 보스-아인슈타인 응축 현상을 관측하기를 오랫동안 열망했지요.
이제 다시 기체 냉각 이야기로 돌아가 봅시다. 여러 개의 전자와 핵으로 구성된 원자도 스핀의 크기에 따라 보손과 페르미온으로 분류됩니다. 간단히 말하면 원자를 구성하는 전자의 스핀과 원자핵의 스핀 값을 다 더한 게 원자의 총 스핀입니다. 총 스핀 값이 정수인 보손 원자를 기체 상태로 포집하여 이를 극도로 낮은 온도로 냉각할 수만 있다면 보스-아인슈타인 응축 현상을 관측할 수 있지 않을까요? 그렇다면 원자 기체의 온도를 어느 정도로 내려야 하는 걸까요?
앞서 설명한 레이저 냉각된 원자 기체의 밀도를 고려하면 보스-아인슈타인 응축을 관측하기 위해서 필요한 기체의 온도는 나노 켈빈 정도로 내려가야 한다는 결론이 나옵니다. 마이크로 켈빈에서 나노 켈빈으로 천 배 정도 기체를 더 냉각하는 것이 과연 가능할까요? 원자의 평균 속도를 수 cm/s에서 수 mm/s로 낮추어야 하는데, 끔찍할 정도로 어려워 보입니다. 그렇지만 물리학자들은 이 놀라운 자연 현상을 관측하겠다는 열망으로 도전하고 또 도전했습니다. 마치 20세기 초 액화 실험에 뛰어든 많은 과학자처럼 말입니다.
실험 도전과 경쟁, 그리고 새로운 발견
이상적인 이론에 따르면 보스-아인슈타인 응측 현상이 어느 임계 온도에서 반드시 발생해야 하는 게 당연했지만, 실제 기체 실험에서 정말로 이 현상을 관측할 수 있을지는 미지수였습니다. 일단 이렇게 낮은 온도에서 원자의 충돌 성질이 어떻게 변모할지 아무도 알 수가 없었습니다. 가장 우려되는 부분은 삼체 결합 현상인데, 앞서 설명하였듯 극도로 낮은 온도에서 기체 상태가 준안정적으로 유지되기 위해서는 원자들의 겹합 반응이 철저히 저지되어야 합니다. 이를 위해서 기체는 아주 낮은 밀도로 유지되어 세 개의 원자가 충돌하는 사건의 빈도를 원천적으로 줄여 액화의 길을 차단해야 하지요. 삼체 충돌 확률은 밀도의 제곱에 비례하기 때문에 기체의 밀도를 낮추면 낮출수록 이런 일은 안 생깁니다.
그렇지만 밀도를 너무 낮추면 이원자 충돌 횟수마저 너무 줄어들게 되고, 그러면 기체가 열평형 상태를 이루는 데 많은 시간이 필요합니다. 열평형이란 걸 간단히 말하면 에너지가 조금 많은 원자가 조금 적은 원자에 에너지를 조금 덜어준다는 것인데, 입자끼리의 충돌이 없으면 이런 에너지 재분배도 일어나지 않습니다. 현실적으로 극복해야 할 또 다른 문제는 극저온 기체를 잘 만들어도 그 수명이 유한하다는 겁니다. 고진공 챔버에서 실험을 한다고는 하지만 상온에 해당하는 배경 기체가 적은 양이나마 공존하고 있고, 이들과 충돌한 극저온 기체 원자는 그야말로 ‘날아가’ 버립니다. 애써 만든 극저온 시료가 증발해버리는 셈이지요. 그뿐 아니라 기체의 밀도를 낮추게 되면 보스-아인슈타인 응축 현상이 발생하는 임계 온도도 함께 낮아지기 때문에 냉각 실험을 하기가 그만큼 부담스럽습니다. 아무도 가보지 않은 전인미답의 영역을 개척하는 실험 물리학자의 마음은 좀 복잡합니다.
어떤 원자를 사용하는 게 가장 좋을까요? 1970년대 중반, 스핀이 한 방향으로 편극된 수소 원자는 다른 수소 원자와 결합된 상태가 존재하지 않고, 따라서 절대 영도에서도 기체 상태로 남아 있을 수 있다는 주장이 제시되었고, 이를 바탕으로 전통적인 극저온 냉각기를 이용한 수소 기체 실험이 여러 연구실에서 추진되었습니다. 초유체 헬륨 막으로 덮인 셀 안에 수소 기체를 압축하는 방식으로 진행된 이 실험은 보스-아인슈타인 응축 조건에 근접하는 듯 보였으나 결국 응축을 보이는 데는 실패했습니다.
셀이 차가워지면서 수소가 헬륨 막에 붙는 일이 발생했고, 수소 밀도가 충분히 높게 유지되지 못하면서 응축에 필요한 밀도 임계 조건에 도달하지 못했던 게 이유였지요. 셀의 온도를 조금 올려 표면에 수소가 붙는 일을 저지하려고 했지만, 이때에는 응축 임계 조건을 만족하기 위한 수소 밀도 값이 커져 삼체 결합을 통해 수소 분자 형성을 무시할 수 없게 되고 따라서 수소 밀도를 원하는 수준으로 유지할 수 없었습니다. 아래위로 꽉 막힌 형국이 된 것이지요.
1980년대 후반, 수소 기체 냉각 실험에서 아주 중요한 두 개의 아이디어가 제안됩니다. 첫째는 스핀 편극된 수소 기체를 자기장 트랩에 가두어 냉각기 표면과의 접촉을 차단하는 방안이고, 둘째는 이렇게 포획된 기체에 증발 냉각 기법을 적용하는 것입니다. 증발 냉각이란 원자 기체를 구성하는 원자 중에 특별히 빠르게 움직이는 원자가 있으면 이것들을 선택적으로 제거함으로써 남아 있는 원자들의 평균 운동 에너지를 낮추는 효과를 내는 방법입니다. 원자를 가둔 자기장 트랩을 벗어나려면 일정 수준 이상의 에너지가 필요합니다. 결국 이 트랩을 벗어나 소실되는 수소는 충분히 운동 에너지가 크고, 벗어나지 못하는 수소는 에너지가 그만큼 작다는 뜻입니다.
뜨거운 커피를 빨리 식히기 위해 컵 뚜껑을 열어 놓는 것과 정확히 같은 이유입니다. 이런 실험 기술의 도입 덕분에 수소 기체를 이용한 연구는 새로운 국면을 맞이하게 됩니다. 90년대 초, 100 마이크로 켈빈의 온도에서 임계 밀도의 20%까지 수소 기체의 밀도를 높이는 성과를 보이게 되지요. 그러나 아쉽게도 증발 냉각을 거치면서 남아 있는 기체 시료의 크기 자체가 줄어들었고, 남은 시료의 상태를 확인하는 측정 신호의 세기도 함께 작아지는 등 실험의 어려움이 생겼습니다.
이와 동시에 수소 원자가 아닌 레이저 냉각된 원자 기체를 사용하는 실험이 80년대 후반 이후 발전하면서 새로운 경쟁 시스템으로 급부상합니다. 수소 기체 실험에서 사용된 자기장 트랩과 증발 냉각의 아이디어가 레이저 냉각된 기체 시료에 그대로 적용되었고, 이는 전통적인 극저온 냉각기를 이용한 실험에 비해 상대적으로 수행하기가 편했기 때문에 더 빠르게 추진될 수 있었습니다. 레이저 냉각 실험이 쉬운 실험은 아니지만, 전통적인 극저온 냉각기를 사용하는 실험과 비교하면 불평할 수준은 아닙니다.
자기장 트랩을 변형하고 싶다고 할 때, 진공 챔버 주변으로 설치된 전류 도선을 새것으로 간단히 교체하면 되었고, 더욱이 기체 시료를 직접 사진 찍는 것도 가능했기 때문에 증발 냉각으로 작아진 시료 크기는 카메라의 배율을 높여 측정하는 방식으로 보상할 수 있었습니다. (여기서 ‘간단히’라는 표현은 2~3명의 연구자가 1~2주 정도 작업하는 것을 의미합니다.) 그렇지만 여전히 저온 원자들 사이의 충돌 성질이 완벽히 알려지지 않은 상황이어서 이러한 시도의 성공 여부는 아무도 장담할 수 없었습니다. 실험에는 레이저 냉각 성질이 우수한 알칼리 원자들, 소듐, 루비듐, 리튬 등이 사용되었고, 세계 유수 대학의 연구 그룹들이 본격적으로 기체 상태의 BEC 생성을 위한 실험 경쟁에 돌입하였습니다.
다행히도 몇몇 알칼리 원자들의 충동 성질이 자기장 트랩에서 증발 냉각을 수행하기에 적절한 것으로 밝혀졌고, 매해 여러 연구 그룹들이 기체 시료 상태를 응축 임계점에 점점 접근시키는 결과를 보고하였습니다. 1995년 즈음이 되어서는 이제 언제, 어느 연구팀이 최초로 양자 기체의 BEC 생성을 관측하는 데 성공했다고 선언할지 모르는 상황이 되었지요. 기체 밀도를 2~3배만 더 올리면 BEC 임계점에 도달하는 지경에 이르렀을 때는 매 학술행사가 긴장감과 기대감의 연속이었다고 합니다.
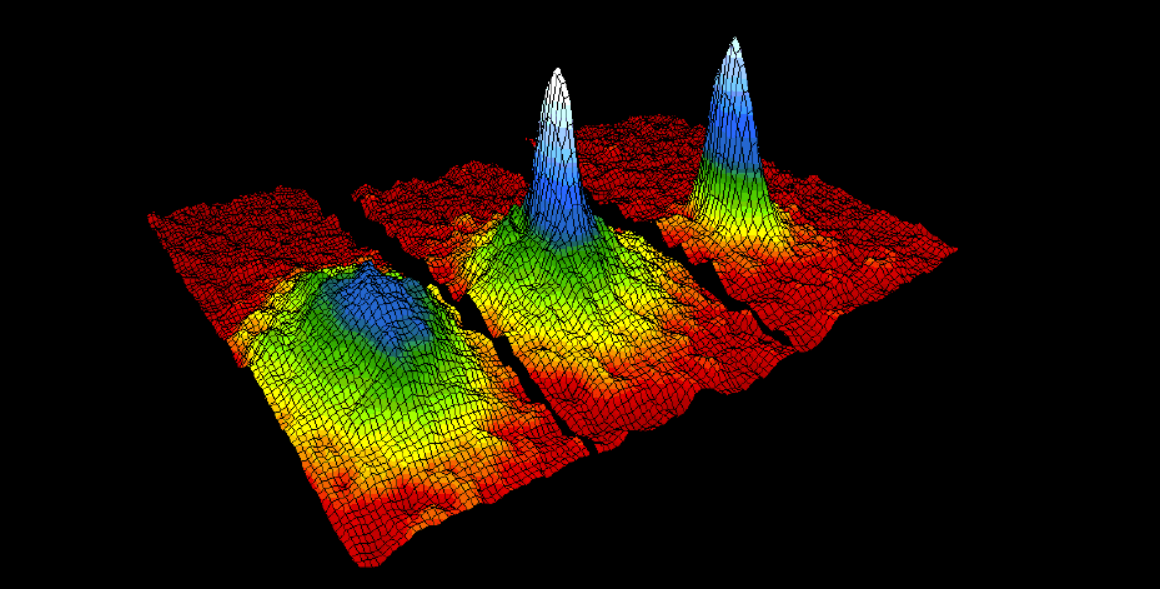
드디어 1995년 7월 14일, 사이언스지에 논문 한 편이 발표됩니다. 이 논문의 제목은 ‘Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor’이고, 논문의 마지막 두 저자는 콜로라도 대학의 칼 와이먼Carl Wieman과 에릭 코넬Eric Cornell이었습니다. 논문 그림 중에는 온도에 따라 측정된 루비듐 기체의 운동량 분포 사진이 있습니다. 온도가 어느 임계 온도 이하로 내려갈 때, 시료의 중앙부에 많은 수의 원자들이 몰리며 뚜렷하게 응집체를 형성하는 것이 관측되었습니다. 이것이 바로 BEC입니다. 1925년에 아인슈타인이 예측한 물리 현상이 70년 만에 처음으로 직접 관측된 것이지요. 흥미롭게도 이 논문이 제출된 날짜는 6월 26일이고 게재가 확정된 것은 6월 29일입니다. 단 3일 만에 게재가 결정된 것입니다. 전해지는 이야기에 따르면, 그 당시 학술지 편집장이 심사자들에게 요구한 심사평은 오직 ‘Yes’ 아니면 ‘No’ 둘 중 하나를 선택하라는 것이었다고 합니다.
이로부터 약 두 달이 지나 MIT의 볼프강 케털리Wolfgang Ketterle교수팀도 소듐 원자로 BEC를 구현하게 됩니다. 사이언스지에 논문을 투고하기 직전 코넬 교수는 자신의 결과를 그해 6월 이탈리아의 카프리섬에서 열린 국제 레이저 분광학회에서 처음 발표하였습니다. 학회 첫날 아침 첫 시간에 코넬의 초청 강연이 있었고, 이어서 경쟁자였던 MIT 케털리 교수의 발표가 예정되었는데, 케털리 교수는 나타나지 않았다고 합니다. 학술행사에서 예고 없이 연사가 나타나지 않는 일이 흔한 일이 아니라서 학회에 참석한 많은 학자 사이에 설왕설래가 있었는데, 케털리 교수가 그 시간까지 밤을 새워 가며 실험하고 있었음이 곧 알려졌습니다. 공동 1등이 되느냐 영원한 2등이 되느냐의 순간이었던 것 같습니다.
또 다른 유력 경쟁 그룹으로는 라이스대학Rice Univ.의 랜달 헐렛Randall Hulet교수팀이 있었습니다. 이들은 앞선 두 팀과 달리 리튬 원자에 주목했었는데 아쉽게도 리튬 원자는 저온에서 서로 잡아당기는 상호작용을 하는 바람에 안정적으로 임계 현상을 보기 어렵다는 게 나중에야 알려졌습니다. 그렇지만 각고의 노력으로 1997년에 리튬 원자에서도 BEC 현상을 관측하였습니다. 이러한 레이저 냉각 기체 실험의 성공 가운데 수소 기체의 BEC 응축도 1998년 MIT의 토마스 그레이탁Thomas Greytak과 다니엘 클레프너Daniel Kleppner 교수 연구팀이 드디어 성공합니다. 비록 첫 번째 BEC 관측이라는 명성은 레이저 냉각 기체 시스템이 가져갔지만, 20년간의 경주를 성공적으로 마치는 순간이었고, 많은 연구자의 마음을 흡족하게 하였습니다.
2001년 노벨 물리학상은 이 새로운 물질 상태를 실험실에서 구현한 세 물리학자, 에릭 코넬과 칼 와이먼, 그리고 볼프강 케털리에게 돌아갔습니다. 보통 노벨상은 업적이 나온 뒤 수십 년이 지난 후 받는다고 해서 우스갯소리로 오래 살아야 받을 수 있다고도 합니다. 6년 만에 노벨상이 주어졌다는 것은 기체 상태의 BEC 관측이 그만큼 오랫동안 기다려온 결과라는 것을 보여줍니다.
한가지 궁금한 점이 생길 수 있는데, 케털리 교수는 비록 2개월 차이이긴 하지만 두 번째로 BEC를 관측하였는데 어떻게 노벨상을 함께 받을 수 있었던 것일까요? 이들의 노벨상 인용문은 “for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms, and for early fundamental studies of the properties of the condensates.”입니다. 초기 BEC 생성뿐만 아니라 BEC의 성질을 연구한 것도 노벨상 수여의 이유 중 하나인데, 케털리 교수는 이 대목에서 최고의 업적을 남겼습니다. 바로 BEC가 거대 물질파라는 사실을 실험으로 보인 것입니다.
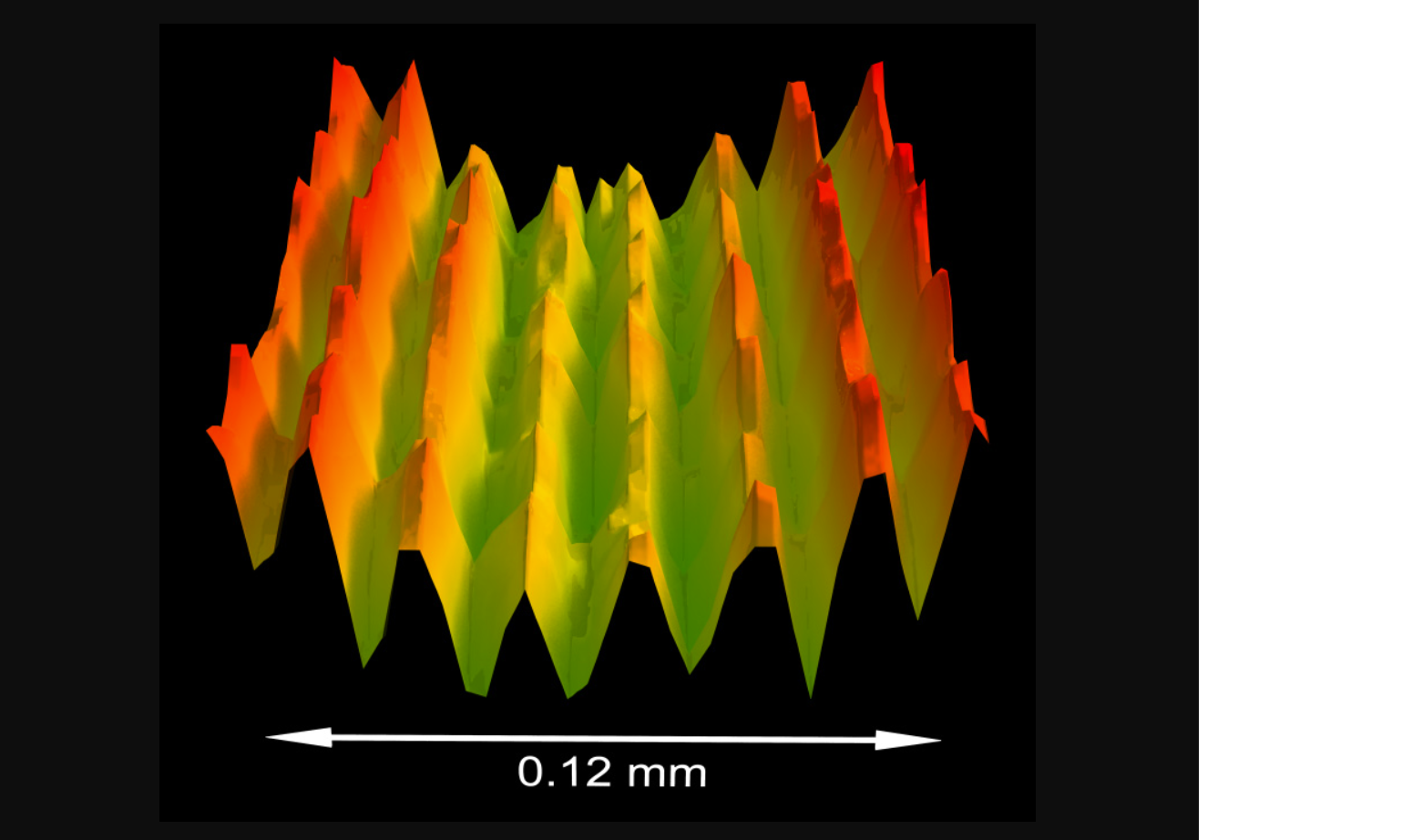
케털리 교수 연구팀은 1997년에 두 개의 독립적인 BEC를 만들어 이들을 공간 상에서 겹쳐보는 실험을 수행하였습니다. 자기장 트랩 가운데에 레이저 빔 장벽을 설치하여 두 개의 분리된 공간을 마련한 뒤 두 곳에서 각각 BEC를 생성하였습니다. 그 후 자기장 트랩과 레이저 빔을 동시에 끕니다. 두 BEC는 자유팽창을 하며 커지다가 서로 겹치게 되는데, 연구팀은 이 겹치는 영역에서 원자 구름이 간섭무늬를 형성하는 것을 직접 관측하였습니다. 많은 수의 원자들이 동일한 양자상태를 공유하면서 거대한 물질파 덩어리를 형성한 것이지요. 두 개의 전구에서 나오는 빛을 벽면에 겹쳐 놓으면 간섭무늬가 만들어지지 않지만, 레이저 빔 두 개를 벽면에 겹쳐 놓으면 간섭무늬가 생긴다는 것을 알고 있을 겁니다. 이런 의미에서 BEC를 ‘원자 레이저’라고도 부릅니다.
저는 학부생이었던 시절, 어느 과학 월간지의 최신연구 소식란에서 BEC 간섭 사진을 처음 보았습니다. 그때의 묘한 감동을 잊을 수가 없습니다. 양자역학 수업에서 입자가 파동성을 갖는다는 것은 배웠습니다. 그리고 간섭 현상과 터널링 현상도 배우고, 문제도 풀면서 나름대로 물질의 파동성에 대해 이해하고 있다고 생각했습니다. 그렇지만 막상 수백만 개의 원자가 마치 하나의 파동처럼 움직이며 간섭 무늬를 만들어 내는 장면을 직접 사진으로 대면했을 때, 요즘 말로 하면 소위 ‘현타’가 오는 것을 느꼈습니다. 양손에 모래를 한 주먹씩 쥐고 책상 위에 뿌렸을 때, 결코 물결무늬가 반복적으로 나오지 않습니다. 더욱이 BEC의 크기가 수 mm나 된다는데, 이건 결국 파동함수가 눈에 보인다는 뜻이지요. 눈에 보이는 파동함수란 걸 누가 상상이나 해 보았겠습니까? 이후 저는 극저온 원자 기체 실험 분야에 매료되었고, 결국에는 MIT의 케털리 교수 연구실에서 박사학위 연구를 하게 되었지요. 제가 유학 생활을 시작한 것은 2001년 8월이었습니다. 지도교수가 노벨상을 받은 것은 그해 11월이었는데, 만일 한 해라도 늦게 갔더라면 연구실에 들어가지 못하지 않았을까 싶습니다. 마치 막차를 탄 듯한 느낌이네요.
극저온 원자 기체 연구와 그 쓸모
지난 25년간 극저온 원자 기체 실험기술은 레이저 기술과 더불어 급격하게 발전하였습니다. 초기 연구 때 보다 훨씬 쉽게 다양한 원자를 대상으로 극저온 기체 시료가 생성되고 있습니다. 심지어 이제는 두 개의 원자 기체 시료를 이용하여 극저온 분자 기체 시료를 만들려는 노력도 한창입니다. 마치 원자를 레고 블록처럼 갖고 놀고 싶어 하는 것 같지요.
새로운 원자 제어 기술이 개발되면서 극저온 원자 기체 시료를 이용한 연구의 범위도 다양한 방향으로 확장되고 있습니다. 대표적인 예로 광격자optical lattices기술이 있습니다. 원자는 레이저 빔 세기에 비례하는 포텐셜 에너지를 갖는데, 만일 여러 개의 레이저 빔이 교차하여 간섭무늬를 만드는 경우, 원자는 이 간섭무늬에 맞춰 주기적인 격자 포텐셜을 느끼게 됩니다. 마치 전자들이 고체 결정 안에서 느끼는 환경과 비슷한 환경을 원자들이 경험하게 되는 것이지요. 레이저 빔의 배열과 세기를 조절하면, 다양한 격자 구조를 만들 수 있고, 그뿐만 아니라 격자의 결합 상수도 제어할 수 있습니다. 최근 광격자 실험에서는 격자 결합 상수가 작아지면서 원자 기체 시스템이 초유체에서 절연체로 변하는 이른바 모트Mott상전이 현상도 관측된 바 있습니다.
또 다른 핵심 기술로 외부 자기장으로 원자 간 상호작용의 세기를 조절하는 기술이 있습니다. 이를 이용하여 자연이 허락하는 최대치의 상호작용을 갖는 페르미 기체가 최근 구현되었고, 여기서 초유체 상전이 임계 온도가 무려 페르미 온도의 15%에 해당하는 사례를 확인한 바 있습니다. 이밖에 레이저 빔을 이용하여 스핀-궤도 결합 효과나 자기장 효과를 인공적으로 만들어 내는 기술도 존재합니다. 이 덕분에 이른바 위상학적 양자 물성이란 걸 원자 기체에서도 연구할 수 있게 되었습니다. 또한 자기 쌍극자 모멘트에 의한 원거리 상호작용 갖는 원자 기체도 생성되었는데 이 실험 연구에서는 초고체성supersolidity연구의 서막을 알리는 결과들이 발표되기도 하였습니다.
이렇듯 다양하게 제어 가능한 극저온 원자 기체를 이용한 양자 다체계 현상 연구는 양자 흉내 내기quantum simulation라는 큰 틀 안에서 지속적으로 발전할 것 같습니다. 고온 초전도체나 양자 자성체 등의 물질은 우수한 성질로 인해 발견 초기부터 많은 관심을 받아왔으나, 이에 대한 완벽한 이해는 여전히 현대 물리학의 난제로 남아 있습니다. 양자 물성의 중심 원리를 찾기 위하여 간단한 모형 이론에 근거한 접근들이 그동안 많이 있었지만, 막상 실재 물질을 이용한 실험 연구 결과를 보면 실험 변수들에 대한 통제도 쉽지 않고 완벽하게 깨끗한 시료를 만드는 것도 불가능하기 때문에 모형에 대한 충분한 검증을 하기에는 한계가 있습니다. 게다가 그 간단한 모형이란 것조차 답이 정확하게 알려진 경우가 많지 않습니다. 바로 이 지점에서 양자 흉내내기 연구의 필요성이 등장합니다. 고도의 실험 변수 통제가 가능한 극저온 원자 기체를 이용하여 어떤 모형 이론이 제안하는 물리계를 정확히 구현하고, 이를 통해 예견되는 양자 물성을 정밀하게 검증할 수 있다면 물리학 발전에 큰 도움이 될 겁니다.
끝으로 나노 켈빈보다 더 낮은 온도로 원자 기체를 더 강력하게 냉각하는 새로운 방법은 없을지 질문을 던져 봅니다. 레이저 냉각 기술이 발명되면서 원자 분광학이 도약적으로 발전하였고, 증발 냉각 기술이 도입되면서 비로소 나노 켈빈의 양자 기체가 구현될 수 있었습니다. 더 광범위한 양자 물성 연구를 위한 새로운 냉각 기술의 도입은 현재 양자 기체 학계의 공통된 기대이며 요구입니다. 절대 영도에 가까워지려는 노력에 획기적인 성과가 있을 때마다 물리학 발전에 큰 이정표들이 세워졌습니다. 앞선 레이저 냉각과 증발 냉각 방식처럼 의외로 간단한 착상에서 새로운 냉각 방식이 발견될 수 있을지도 모릅니다.